Home » Mathematik (Page 2)
Category Archives: Mathematik
Winkel und Abstände III
III- Abstände – Hessesche Normalenform
-
Berechne den Abstand zwischen der Ebene $E$ und dem Punkt $P$.
$ 3x-2y+4z=10 $ $\:\:$ und $\:\:$ $ P(2|3|1) $
Lösung$ 3x-2y+4z=10 $ $\:\:$ und $\:\:$ $ P(2|3|1) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Normalenvektor\: von\: E\: ablesen $
$\qquad$ $ \vec{n_E}= \begin{pmatrix} 3\\-2\\4 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Ebenengleichung\: umstellen $
$\qquad$ $ 3x-2y+4z-10=0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Abstand\: berechnen $
$\qquad$ $ d_{(P,E)}= $ $ \begin{vmatrix} \frac{3\cdot 2-2\cdot 3+4\cdot 1-10} { \begin{vmatrix} \begin{pmatrix} 3\\-2\\4 \end{pmatrix} \end{vmatrix} } \end{vmatrix} = \begin{vmatrix} \frac{-6}{\sqrt{29}} \end{vmatrix} =1,11417 $
$\:\:\:$ Der Abstand zwischen $P$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_{(P,E)}\approx1,1142\: LE $ -
Gebe die Ebene in Hessescher Normalenform an und bestimme die Abstände der Punkte $P,\: Q$ und $R$ von der Ebene.
a) $E:3x+6y-2z=4, \:P(4|-1|2), \:Q(-4|6|4), \:R(6|1|10)$
Lösung$E:3x+6y-2z=4, \:P(4|-1|2), \:Q(-4|6|4), \:R(6|1|10)$
$a_1)$ Abstand $P$ von der Ebene $E$
$ \:\:\:\: $ Seien: $E:3x+6y-2z=4$ $\:$ und $\:$ $\:P(4|-1|2)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Normalenvektor\: n_E\: der\: Ebene\: E\: ablesen $
$\qquad$ $ \vec{n_E}= \begin{pmatrix} 3\\6\\-2 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $ E:3x+6y-2z-4=0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d $
$\qquad$ $ d_{(P,E)}= \begin{vmatrix} \frac{3\cdot 4+6\cdot (-1)-2\cdot 2-4} { \begin{vmatrix} \begin{pmatrix} 3\\6\\-2 \end{pmatrix} \end{vmatrix} } \end{vmatrix} = \frac{2}{7} $
$\:\:\:$ Der Abstand zwischen $P$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_{(P,E)}=\frac{2}{7}\: LE $
$a_2)$ Abstand $Q$ von der Ebene $E$
$ \:\:\:\: $ Seien: $E:3x+6y-2z=4$ $\:$ und $\:$ $\:Q(-4|6|4)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Normalenvektor\: n_E\: der\: Ebene\: E\: ablesen $
$\qquad$ $ \vec{n_E}= \begin{pmatrix} 3\\6\\-2 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $ E:3x+6y-2z-4=0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d $
$\qquad$ $ d_{(Q,E)}= \begin{vmatrix} \frac{3\cdot (-4)+6\cdot 6-2\cdot 4-4} { \begin{vmatrix} \begin{pmatrix} 3\\6\\-2 \end{pmatrix} \end{vmatrix} } \end{vmatrix} = \frac{12}{7} $
$\:\:\:$ Der Abstand zwischen $Q$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_{(Q,E)}=\frac{12}{7}\: LE $
$a_3)$ Abstand $R$ von der Ebene $E$
$ \:\:\:\: $ Seien: $E:3x+6y-2z=4$ $\:$ und $\:$ $\:R(6|1|10)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Normalenvektor\: n_E\: der\: Ebene\: E\: ablesen $
$\qquad$ $ \vec{n_E}= \begin{pmatrix} 3\\6\\-2 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $ E:3x+6y-2z-4=0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d $
$\qquad$ $ d_{((R,E)}= \begin{vmatrix} \frac{3\cdot 6+6\cdot 1-2\cdot 10-4} { \begin{vmatrix} \begin{pmatrix} 3\\6\\-2 \end{pmatrix} \end{vmatrix} } \end{vmatrix} =0 $
$\:\:\:$ Der Abstand zwischen $R$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_{(R,E)}=0\: LE $
b) $ E: \begin{bmatrix} \vec{x}- \begin{pmatrix} 9\\0\\-3 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 4\\4\\-2 \end{pmatrix} =0 $ $\:$ $ \:P(2|2|3), \:Q(4|-1|0), \:R(8|3|2) $
Lösung$b_1)$ Abstand $P$ von der Ebene $E$
$\:\:\:\:$ Seien: $E: \begin{bmatrix} \vec{x}- \begin{pmatrix} 9\\0\\-3 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 4\\4\\-2 \end{pmatrix} $ und $\:P(2|2|3) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Schreibe\: E\: in\: Koordinatenform\: um $
$\qquad$ Multipliziere aus:
$\qquad\qquad$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 4\\4\\-2 \end{pmatrix} = 4x+4y-2z $
$\qquad\qquad$ $ \begin{pmatrix} 9\\0\\-3 \end{pmatrix} \cdot \begin{pmatrix} 4\\4\\-2 \end{pmatrix} = 9\cdot 4+0\cdot 4+(-3)\cdot (-2) =42 $
$\qquad\qquad$ Setzte zusammen für die Koordinatenform ein:
$\qquad\qquad \longrightarrow $ Die Koordinatenform lautet: $ 4x+4y-2z=42 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Normalenvektor\: n_E\: der\: Ebene\: E\: ablesen $
$\qquad$ $ \vec{n_E}= \begin{pmatrix} 4\\4\\-2 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $ E:4x+4y-2z-42=0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d $
$\qquad$ $ d_{(P,E)}= \begin{vmatrix} \frac{4\cdot 2+4\cdot 2+(-2)\cdot 3-42} { \begin{vmatrix} \begin{pmatrix} 3\\4\\-12 \end{pmatrix} \end{vmatrix} } \end{vmatrix} = \begin{vmatrix} \frac{-32}{6} \end{vmatrix} = \frac{16}{3} $
$\:\:\:$ Der Abstand zwischen $P$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_{(P,E)}=\frac{16}{3}\: LE $
$b_2)$ Abstand $Q$ von der Ebene $E$
$\:\:\:\:$ Seien: $E: \begin{bmatrix} \vec{x}- \begin{pmatrix} 9\\0\\-3 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 4\\4\\-2 \end{pmatrix} $ und $\:Q(4|-1|0) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Schreibe\: E\: in\: Koordinatenform\: um $
$\qquad$ Multipliziere aus:
$\qquad\qquad$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 4\\4\\-2 \end{pmatrix} = 4x+4y-2z $
$\qquad\qquad$ $ \begin{pmatrix} 9\\0\\-3 \end{pmatrix} \cdot \begin{pmatrix} 4\\4\\-2 \end{pmatrix} = 9\cdot 4+0\cdot 4+(-3)\cdot (-2) =42 $
$\qquad\qquad$ Setzte zusammen für die Koordinatenform ein:
$\qquad\qquad \longrightarrow $ Die Koordinatenform lautet: $ 4x+4y-2z=42 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Normalenvektor\: n_E\: der\: Ebene\: E\: ablesen $
$\qquad$ $ \vec{n_E}= \begin{pmatrix} 4\\4\\-2 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $ E:4x+4y-2z-42=0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d $
$\qquad$ $ d_{(Q,E)}= \begin{vmatrix} \frac{4\cdot 4+4\cdot (-1)+(-2)\cdot 0-42} { \begin{vmatrix} \begin{pmatrix} 3\\4\\-12 \end{pmatrix} \end{vmatrix} } \end{vmatrix} = \begin{vmatrix} \frac{-30}{6} \end{vmatrix} = 5 $
$\:\:\:$ Der Abstand zwischen $Q$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_{(Q,E)}=5\: LE $
$b_3)$ Abstand $R$ von der Ebene $E$
$\:\:\:\:$ Seien: $E: \begin{bmatrix} \vec{x}- \begin{pmatrix} 9\\0\\-3 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 4\\4\\-2 \end{pmatrix} $ und $\:R(8|3|2) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Schreibe\: E\: in\: Koordinatenform\: um $
$\qquad$ Multipliziere aus:
$\qquad\qquad$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 4\\4\\-2 \end{pmatrix} = 4x+4y-2z $
$\qquad\qquad$ $ \begin{pmatrix} 9\\0\\-3 \end{pmatrix} \cdot \begin{pmatrix} 4\\4\\-2 \end{pmatrix} = 9\cdot 4+0\cdot 4+(-3)\cdot (-2) =42 $
$\qquad\qquad$ Setzte zusammen für die Koordinatenform ein:
$\qquad\qquad \longrightarrow $ Die Koordinatenform lautet: $ 4x+4y-2z=42 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Normalenvektor\: n_E\: der\: Ebene\: E\: ablesen $
$\qquad$ $ \vec{n_E}= \begin{pmatrix} 4\\4\\-2 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $ E:4x+4y-2z-42=0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d $
$\qquad$ $ d_{(R,E)}= \begin{vmatrix} \frac{4\cdot 8+4\cdot 3+(-2)\cdot 2-42} { \begin{vmatrix} \begin{pmatrix} 3\\4\\-12 \end{pmatrix} \end{vmatrix} } \end{vmatrix} = \begin{vmatrix} \frac{-2}{6} \end{vmatrix} = \frac{1}{3} $
$\:\:\:$ Der Abstand zwischen $R$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_{(R,E)}=\frac{1}{3}\: LE $
$c)$ $ E:3x+4y-12z=6,\: P(1|2|5),\: Q(-2|4|1),\: R(6|3|2) $
Lösung$c_1)$ Abstand $P$ von der Ebene $E$
$\:\:\:\:$ Seien: $E:3x+4y-12z=6\:$ und $\:P(1|2|5) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Normalenvektor\: n_E\: der\: Ebene\: E\: ablesen $
$\qquad$ $ \vec{n_E}= \begin{pmatrix} 3\\4\\-12 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $ E:3x+4y-12z-6=0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d $
$\qquad$ $ d_{(P,E)}= \begin{vmatrix} \frac{3\cdot 1+4\cdot 2-12\cdot 5-6} { \begin{vmatrix} \begin{pmatrix} 3\\4\\-12 \end{pmatrix} \end{vmatrix} } \end{vmatrix} = \begin{vmatrix} \frac{-55}{13} \end{vmatrix} = \frac{55}{13} $
$\:\:\:$ Der Abstand zwischen $P$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_{(P,E)}=\frac{55}{13}\: LE $
$c_2)$ Abstand $Q$ von der Ebene $E$
$\:\:\:\:$ Seien: $E:3x+4y-12z=6\:$ und $\:Q(-2|4|1) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Normalenvektor\: n_E\: der\: Ebene\: E\: ablesen $
$\qquad$ $ \vec{n_E}= \begin{pmatrix} 3\\4\\-12 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $ E:3x+4y-12z-6=0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d $
$\qquad$ $ d_{(Q,E)}= \begin{vmatrix} \frac{3\cdot (-2)+4\cdot 4-12\cdot 1-6} { \begin{vmatrix} \begin{pmatrix} 3\\4\\-12 \end{pmatrix} \end{vmatrix} } \end{vmatrix} = \begin{vmatrix} \frac{-8}{13} \end{vmatrix} = \frac{8}{13} $
$\:\:\:$ Der Abstand zwischen $Q$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_{(Q,E)}=\frac{8}{13}\: LE $
$c_3)$ Abstand $R$ von der Ebene $E$
$\:\:\:\:$ Seien: $E:3x+4y-12z=6\:$ und $\:R(6|3|2) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Normalenvektor\: n_E\: der\: Ebene\: E\: ablesen $
$\qquad$ $ \vec{n_E}= \begin{pmatrix} 3\\4\\-12 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $ E:3x+4y-12z-6=0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d $
$\qquad$ $ d_{(R,E)}= \begin{vmatrix} \frac{3\cdot 6+4\cdot 3-12\cdot 2-6} { \begin{vmatrix} \begin{pmatrix} 3\\4\\-12 \end{pmatrix} \end{vmatrix} } \end{vmatrix} = \begin{vmatrix} \frac{0}{13} \end{vmatrix} = 0 $
$\:\:\:$ Der Abstand zwischen $R$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_{(R,E)}=0\: LE $ -
Gegeben seien die drei Punkte $A(1|1|1),\: B(3|2|-2),\: C(-1|0|3)$.
a) Bestimme eine Normalenform der Ebene E, die durch diese drei Punkte gegeben ist.
b) Bestimme die Hessesche Normalenform von $E$ und berechne den Abstand der Ebene vom Koordinatenursprung.
LösungPunkte $A(1|1|1),\: B(3|2|-2),\: C(-1|0|3)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebene\: E\: in\: Parameterform\: ein $
$\qquad$ $ E:\vec{x}= \begin{pmatrix} 1\\1\\1 \end{pmatrix} + r\cdot \begin{pmatrix} 3-1\\2-1\\-2-1 \end{pmatrix} + s\cdot \begin{pmatrix} -1-1\\0-1\\3-1 \end{pmatrix} = \underline{ \begin{pmatrix} 1\\1\\1 \end{pmatrix} + r\cdot \begin{pmatrix} 2\\1\\-3 \end{pmatrix} + s\cdot \begin{pmatrix} -2\\-1\\2 \end{pmatrix} } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebene\: E\: in\: Normalenform\: ein $
$\qquad$ Kreuzprodukt der Richtungsvektoren:
$\qquad$ $ d= \begin{pmatrix} 2\\1\\-3 \end{pmatrix} \times \begin{pmatrix} -2\\-1\\2 \end{pmatrix} = \begin{pmatrix} 1\cdot 2-(-3)\cdot (-1)\\ (-3)\cdot (-2)-2\cdot 2\\ 2\cdot (-1)-1\cdot (-2) \end{pmatrix} = \begin{pmatrix} -1\\2\\0 \end{pmatrix} $
$\qquad$ Der Ortsvektor: $ \vec{a}= \begin{pmatrix} 1\\1\\1 \end{pmatrix} $
$\qquad$ Die Normalenform (Normalengleichung) von $E$ lautet:
$\qquad$ $ E: \begin{bmatrix} \vec{x}- \begin{pmatrix} 1\\1\\1 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} -1\\2\\0 \end{pmatrix} =0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Bestimme\: die\: Hessesche\: Normalenform $
$\qquad$ $ E: \begin{bmatrix} \vec{x}- \begin{pmatrix} 1\\1\\1 \end{pmatrix} \end{bmatrix} \cdot \frac{1}{\sqrt{(-1)^2+2^2}} \begin{pmatrix} -1\\2\\0 \end{pmatrix} =0 $
$\qquad$ $ \iff E: \begin{bmatrix} \vec{x}- \begin{pmatrix} 1\\1\\1 \end{pmatrix} \end{bmatrix} \cdot \frac{1}{\sqrt{5}} \begin{pmatrix} -1\\2\\0 \end{pmatrix} =0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Bestimme\: der\: Abstand\: des\: Koordinatenursprungs\: O(0|0|0)\: von\: E $
$\qquad$ $ d_{(O,E)}= \begin{vmatrix} – \begin{pmatrix} 1\\1\\1 \end{pmatrix} \cdot \frac{1}{\sqrt{5}} \begin{pmatrix} -1\\2\\0 \end{pmatrix} \end{vmatrix} = \frac{1}{\sqrt{5}} (-1+2) = \frac{1}{\sqrt{5}} $
$\:\:\:$ Der Abstand zwischen $0$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_{(O,E)}=\frac{1}{\sqrt{5}} \: LE $
Mehr Aufgaben
Pyramide
Lösung
$a) $ Höhe von $D$ über $ABC:\:\: E_1:\vec{x}= \overrightarrow{OA}+r\cdot \overrightarrow{AB}+s\cdot \overrightarrow{AC}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Parameterform\: von\: E_1 $
$\qquad$ $ E_1: \vec{x}= \begin{pmatrix} 4\\-1\\1 \end{pmatrix} + r\cdot \begin{pmatrix} 5-4\\4-(-1)\\0-1 \end{pmatrix} + s\cdot \begin{pmatrix} -1-4\\2-(-1)\\2-1 \end{pmatrix} = \underline{ \begin{pmatrix} 4\\-1\\1 \end{pmatrix} + r\cdot \begin{pmatrix} 1\\5\\-1 \end{pmatrix} + s\cdot \begin{pmatrix} -5\\3\\1 \end{pmatrix} } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Koordinatenform\: von\: E_1 $
$\qquad$ Kreuzprodukt der Richtungsvektoren:
$\qquad$ $ d= \begin{pmatrix} 1\\5\\-1 \end{pmatrix} \times \begin{pmatrix} -5\\3\\1 \end{pmatrix} = \begin{pmatrix} 5\cdot 1-(-1)\cdot3\\ (-1)\cdot (-5)-1\cdot 1\\ 1\cdot 3-5\cdot (-5) \end{pmatrix} = \begin{pmatrix} 8\\4\\28 \end{pmatrix} $
$\qquad$ Der Ortsvektor: $\vec{a}= \begin{pmatrix} 4\\-1\\1 \end{pmatrix} $
$\qquad \iff $ Die Normalengleichung lautet: $ E_1: \begin{bmatrix} \vec{x}- \begin{pmatrix} 4\\-1\\1 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 8\\4\\28 \end{pmatrix} =0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Multipliziere\: aus $
$\qquad$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 8\\4\\28 \end{pmatrix} = 8x+4y+28z $
$\qquad$ $ \begin{pmatrix} 4\\-1\\1 \end{pmatrix} \cdot \begin{pmatrix} 8\\4\\28 \end{pmatrix} = 4\cdot 8+(-1)\cdot 4+1\cdot 28 =56 $
$\qquad$ Setzte zusammen:
$\qquad \iff $ Die Koordinatenform lautet: $ E_1: 8x+4y+28z=56\:\: |:4 $
$\qquad \iff E_1:2x+y+7z=14 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Lies\: den\: Normalenvektor\: n_{E_1}\: der\: Ebene\: $
$\qquad$ $ \vec{n_{E_1}}= \begin{pmatrix} 2\\1\\7 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $E_1:2x+y+7z-14=0$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d\: mit\: der\: Hesseschen\: Normalenform $
$\qquad$ $ h=d_D= \begin{vmatrix} \frac {2\cdot 3+1\cdot 3+7\cdot 6-14} { \begin{vmatrix} \begin{pmatrix} 2\\1\\7 \end{pmatrix} \end{vmatrix} } \end{vmatrix} $ = 5,0350
$\:\:\:$ Der Abstand $d$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_D\approx5,04 \: LE $
$b) $ Höhe von $B$ über $ACD:\:\: E_2:\vec{x}= \overrightarrow{OA}+r\cdot \overrightarrow{AC}+s\cdot \overrightarrow{AD}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Parameterform\: von\: E_2 $
$\qquad$ $ E_2: \vec{x}= \begin{pmatrix} 4\\-1\\1 \end{pmatrix} + r\cdot \begin{pmatrix} -1-4\\2-(-1)\\2-1 \end{pmatrix} + s\cdot \begin{pmatrix} 3-4\\3-(-1)\\6-1 \end{pmatrix} = \underline{ \begin{pmatrix} 4\\-1\\1 \end{pmatrix} + r\cdot \begin{pmatrix} -5\\3\\1 \end{pmatrix} + s\cdot \begin{pmatrix} -1\\4\\5 \end{pmatrix} } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Koordinatenform\: von\: E_2 $
$\qquad$ Kreuzprodukt der Richtungsvektoren:
$\qquad$ $ d= \begin{pmatrix} -5\\3\\1 \end{pmatrix} \times \begin{pmatrix} -1\\4\\5 \end{pmatrix} = \begin{pmatrix} 3\cdot 5-1\cdot 4\\ 1\cdot (-1)-(-5)\cdot 5\\ (-5)\cdot 4-3\cdot (-1) \end{pmatrix} = \begin{pmatrix} 11\\24\\-17 \end{pmatrix} $
$\qquad$ Der Ortsvektor: $\vec{a}= \begin{pmatrix} 4\\-1\\1 \end{pmatrix} $
$\qquad \iff $ Die Normalengleichung lautet: $ E_2: \begin{bmatrix} \vec{x}- \begin{pmatrix} 4\\-1\\1 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 11\\24\\-17 \end{pmatrix} =0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Multipliziere\: aus $
$\qquad$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 11\\24\\-17 \end{pmatrix} = 11x+24y-17z $
$\qquad$ $ \begin{pmatrix} 4\\-1\\1 \end{pmatrix} \cdot \begin{pmatrix} 11\\24\\-17 \end{pmatrix} = 4\cdot 11+(-1)\cdot 24+1\cdot (-17) =3 $
$\qquad$ Setzte zusammen:
$\qquad \iff $ Die Koordinatenform lautet: $ E_2: 11x+24y-17z=3 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Lies\: den\: Normalenvektor\: n_{E_2}\: der\: Ebene\: $
$\qquad$ $ \vec{n_{E_2}}= \begin{pmatrix} 11\\24\\-17 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $E_2:11x+24y-17z-3=0$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d\: mit\: der\: Hesseschen\: Normalenform $
$\qquad$ $ h=d_D= \begin{vmatrix} \frac {11\cdot 5+24\cdot 4+(-17)\cdot 0-3} { \begin{vmatrix} \begin{pmatrix} 11\\24\\-17 \end{pmatrix} \end{vmatrix} } \end{vmatrix} $ = 4,7133
$\:\:\:$ Der Abstand $d$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_D\approx4,71 \: LE $
$c) $ Höhe von $A$ über $BCD:\:\: E_3:\vec{x}= \overrightarrow{OB}+r\cdot \overrightarrow{BC}+s\cdot \overrightarrow{CD}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Parameterform\: von\: E_3 $
$\qquad$ $ E_3: \vec{x}= \begin{pmatrix} 5\\4\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -1-5\\2-4\\2-0 \end{pmatrix} + s\cdot \begin{pmatrix} 3-5\\3-4\\6-0 \end{pmatrix} = \underline{ \begin{pmatrix} 5\\4\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -6\\-2\\2 \end{pmatrix} + s\cdot \begin{pmatrix} -2\\-1\\6 \end{pmatrix} } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Koordinatenform\: von\: E_3 $
$\qquad$ Kreuzprodukt der Richtungsvektoren:
$\qquad$ $ d= \begin{pmatrix} -6\\-2\\2 \end{pmatrix} \times \begin{pmatrix} -2\\-1\\6 \end{pmatrix} = \begin{pmatrix} (-2)\cdot 6-2\cdot (-1)\\ 2\cdot (-2)-(-6)\cdot 6\\ (-6)\cdot (-1)-(-2)\cdot (-2) \end{pmatrix} = \begin{pmatrix} -10\\32\\2 \end{pmatrix} $
$\qquad$ Der Ortsvektor: $\vec{a}= \begin{pmatrix} 5\\4\\0 \end{pmatrix} $
$\qquad \iff $ Die Normalengleichung lautet: $ E_3: \begin{bmatrix} \vec{x}- \begin{pmatrix} 5\\4\\0 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} -10\\32\\2 \end{pmatrix} =0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Multipliziere\: aus $
$\qquad$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} -10\\32\\2 \end{pmatrix} = -10x+32y+2z $
$\qquad$ $ \begin{pmatrix} 5\\4\\0 \end{pmatrix} \cdot \begin{pmatrix} -10\\32\\2 \end{pmatrix} = 5\cdot (-10)+4\cdot 32+0\cdot 2 =78 $
$\qquad$ Setzte zusammen:
$\qquad \iff $ Die Koordinatenform lautet: $ E_3: -10x+32y+2z=78 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Lies\: den\: Normalenvektor\: n_{E_3}\: der\: Ebene\: $
$\qquad$ $ \vec{n_{E_3}}= \begin{pmatrix} -10\\32\\2 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $E_3:-10x+32y+2z-78=0$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d\: mit\: der\: Hesseschen\: Normalenform $
$\qquad$ $ h=d_D= \begin{vmatrix} \frac {-10\cdot 4+32\cdot (-1)+2\cdot 1-78} { \begin{vmatrix} \begin{pmatrix} -10\\32\\2 \end{pmatrix} \end{vmatrix} } \end{vmatrix} $ = 4,4067
$\:\:\:$ Der Abstand $d$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_D\approx4,41 \: LE $
$c) $ Höhe von $A$ über $BCD:\:\: E_3:\vec{x}= \overrightarrow{OB}+r\cdot \overrightarrow{BC}+s\cdot \overrightarrow{CD}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Parameterform\: von\: E_3 $
$\qquad$ $ E_3: \vec{x}= \begin{pmatrix} 5\\4\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -1-5\\2-4\\2-0 \end{pmatrix} + s\cdot \begin{pmatrix} 3-5\\3-4\\6-0 \end{pmatrix} = \underline{ \begin{pmatrix} 5\\4\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -6\\-2\\2 \end{pmatrix} + s\cdot \begin{pmatrix} -2\\-1\\6 \end{pmatrix} } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Koordinatenform\: von\: E_3 $
$\qquad$ Kreuzprodukt der Richtungsvektoren:
$\qquad$ $ d= \begin{pmatrix} -6\\-2\\2 \end{pmatrix} \times \begin{pmatrix} -2\\-1\\6 \end{pmatrix} = \begin{pmatrix} (-2)\cdot 6-2\cdot (-1)\\ 2\cdot (-2)-(-6)\cdot 6\\ (-6)\cdot (-1)-(-2)\cdot (-2) \end{pmatrix} = \begin{pmatrix} -10\\32\\2 \end{pmatrix} $
$\qquad$ Der Ortsvektor: $\vec{a}= \begin{pmatrix} 5\\4\\0 \end{pmatrix} $
$\qquad \iff $ Die Normalengleichung lautet: $ E_3: \begin{bmatrix} \vec{x}- \begin{pmatrix} 5\\4\\0 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} -10\\32\\2 \end{pmatrix} =0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Multipliziere\: aus $
$\qquad$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} -10\\32\\2 \end{pmatrix} = -10x+32y+2z $
$\qquad$ $ \begin{pmatrix} 5\\4\\0 \end{pmatrix} \cdot \begin{pmatrix} -10\\32\\2 \end{pmatrix} = 5\cdot (-10)+4\cdot 32+0\cdot 2 =78 $
$\qquad$ Setzte zusammen:
$\qquad \iff $ Die Koordinatenform lautet: $ E_3: -10x+32y+2z=78 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Lies\: den\: Normalenvektor\: n_{E_3}\: der\: Ebene\: $
$\qquad$ $ \vec{n_{E_3}}= \begin{pmatrix} -10\\32\\2 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $E_3:-10x+32y+2z-78=0$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d\: mit\: der\: Hesseschen\: Normalenform $
$\qquad$ $ h=d_D= \begin{vmatrix} \frac {-10\cdot 4+32\cdot (-1)+2\cdot 1-78} { \begin{vmatrix} \begin{pmatrix} -10\\32\\2 \end{pmatrix} \end{vmatrix} } \end{vmatrix} $ = 4,4067
$\:\:\:$ Der Abstand $d$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_D\approx4,41 \: LE $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Parameterform\: von\: E_1 $
$\qquad$ $ E_1: \vec{x}= \begin{pmatrix} 4\\-1\\1 \end{pmatrix} + r\cdot \begin{pmatrix} 5-4\\4-(-1)\\0-1 \end{pmatrix} + s\cdot \begin{pmatrix} -1-4\\2-(-1)\\2-1 \end{pmatrix} = \underline{ \begin{pmatrix} 4\\-1\\1 \end{pmatrix} + r\cdot \begin{pmatrix} 1\\5\\-1 \end{pmatrix} + s\cdot \begin{pmatrix} -5\\3\\1 \end{pmatrix} } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Koordinatenform\: von\: E_1 $
$\qquad$ Kreuzprodukt der Richtungsvektoren:
$\qquad$ $ d= \begin{pmatrix} 1\\5\\-1 \end{pmatrix} \times \begin{pmatrix} -5\\3\\1 \end{pmatrix} = \begin{pmatrix} 5\cdot 1-(-1)\cdot3\\ (-1)\cdot (-5)-1\cdot 1\\ 1\cdot 3-5\cdot (-5) \end{pmatrix} = \begin{pmatrix} 8\\4\\28 \end{pmatrix} $
$\qquad$ Der Ortsvektor: $\vec{a}= \begin{pmatrix} 4\\-1\\1 \end{pmatrix} $
$\qquad \iff $ Die Normalengleichung lautet: $ E_1: \begin{bmatrix} \vec{x}- \begin{pmatrix} 4\\-1\\1 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 8\\4\\28 \end{pmatrix} =0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Multipliziere\: aus $
$\qquad$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 8\\4\\28 \end{pmatrix} = 8x+4y+28z $
$\qquad$ $ \begin{pmatrix} 4\\-1\\1 \end{pmatrix} \cdot \begin{pmatrix} 8\\4\\28 \end{pmatrix} = 4\cdot 8+(-1)\cdot 4+1\cdot 28 =56 $
$\qquad$ Setzte zusammen:
$\qquad \iff $ Die Koordinatenform lautet: $ E_1: 8x+4y+28z=56\:\: |:4 $
$\qquad \iff E_1:2x+y+7z=14 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Lies\: den\: Normalenvektor\: n_{E_1}\: der\: Ebene\: $
$\qquad$ $ \vec{n_{E_1}}= \begin{pmatrix} 2\\1\\7 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $E_1:2x+y+7z-14=0$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d\: mit\: der\: Hesseschen\: Normalenform $
$\qquad$ $ h=d_D= \begin{vmatrix} \frac {2\cdot 3+1\cdot 3+7\cdot 6-14} { \begin{vmatrix} \begin{pmatrix} 2\\1\\7 \end{pmatrix} \end{vmatrix} } \end{vmatrix} $ = 5,0350
$\:\:\:$ Der Abstand $d$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_D\approx5,04 \: LE $
$b) $ Höhe von $B$ über $ACD:\:\: E_2:\vec{x}= \overrightarrow{OA}+r\cdot \overrightarrow{AC}+s\cdot \overrightarrow{AD}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Parameterform\: von\: E_2 $
$\qquad$ $ E_2: \vec{x}= \begin{pmatrix} 4\\-1\\1 \end{pmatrix} + r\cdot \begin{pmatrix} -1-4\\2-(-1)\\2-1 \end{pmatrix} + s\cdot \begin{pmatrix} 3-4\\3-(-1)\\6-1 \end{pmatrix} = \underline{ \begin{pmatrix} 4\\-1\\1 \end{pmatrix} + r\cdot \begin{pmatrix} -5\\3\\1 \end{pmatrix} + s\cdot \begin{pmatrix} -1\\4\\5 \end{pmatrix} } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Koordinatenform\: von\: E_2 $
$\qquad$ Kreuzprodukt der Richtungsvektoren:
$\qquad$ $ d= \begin{pmatrix} -5\\3\\1 \end{pmatrix} \times \begin{pmatrix} -1\\4\\5 \end{pmatrix} = \begin{pmatrix} 3\cdot 5-1\cdot 4\\ 1\cdot (-1)-(-5)\cdot 5\\ (-5)\cdot 4-3\cdot (-1) \end{pmatrix} = \begin{pmatrix} 11\\24\\-17 \end{pmatrix} $
$\qquad$ Der Ortsvektor: $\vec{a}= \begin{pmatrix} 4\\-1\\1 \end{pmatrix} $
$\qquad \iff $ Die Normalengleichung lautet: $ E_2: \begin{bmatrix} \vec{x}- \begin{pmatrix} 4\\-1\\1 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 11\\24\\-17 \end{pmatrix} =0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Multipliziere\: aus $
$\qquad$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 11\\24\\-17 \end{pmatrix} = 11x+24y-17z $
$\qquad$ $ \begin{pmatrix} 4\\-1\\1 \end{pmatrix} \cdot \begin{pmatrix} 11\\24\\-17 \end{pmatrix} = 4\cdot 11+(-1)\cdot 24+1\cdot (-17) =3 $
$\qquad$ Setzte zusammen:
$\qquad \iff $ Die Koordinatenform lautet: $ E_2: 11x+24y-17z=3 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Lies\: den\: Normalenvektor\: n_{E_2}\: der\: Ebene\: $
$\qquad$ $ \vec{n_{E_2}}= \begin{pmatrix} 11\\24\\-17 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $E_2:11x+24y-17z-3=0$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d\: mit\: der\: Hesseschen\: Normalenform $
$\qquad$ $ h=d_D= \begin{vmatrix} \frac {11\cdot 5+24\cdot 4+(-17)\cdot 0-3} { \begin{vmatrix} \begin{pmatrix} 11\\24\\-17 \end{pmatrix} \end{vmatrix} } \end{vmatrix} $ = 4,7133
$\:\:\:$ Der Abstand $d$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_D\approx4,71 \: LE $
$c) $ Höhe von $A$ über $BCD:\:\: E_3:\vec{x}= \overrightarrow{OB}+r\cdot \overrightarrow{BC}+s\cdot \overrightarrow{CD}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Parameterform\: von\: E_3 $
$\qquad$ $ E_3: \vec{x}= \begin{pmatrix} 5\\4\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -1-5\\2-4\\2-0 \end{pmatrix} + s\cdot \begin{pmatrix} 3-5\\3-4\\6-0 \end{pmatrix} = \underline{ \begin{pmatrix} 5\\4\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -6\\-2\\2 \end{pmatrix} + s\cdot \begin{pmatrix} -2\\-1\\6 \end{pmatrix} } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Koordinatenform\: von\: E_3 $
$\qquad$ Kreuzprodukt der Richtungsvektoren:
$\qquad$ $ d= \begin{pmatrix} -6\\-2\\2 \end{pmatrix} \times \begin{pmatrix} -2\\-1\\6 \end{pmatrix} = \begin{pmatrix} (-2)\cdot 6-2\cdot (-1)\\ 2\cdot (-2)-(-6)\cdot 6\\ (-6)\cdot (-1)-(-2)\cdot (-2) \end{pmatrix} = \begin{pmatrix} -10\\32\\2 \end{pmatrix} $
$\qquad$ Der Ortsvektor: $\vec{a}= \begin{pmatrix} 5\\4\\0 \end{pmatrix} $
$\qquad \iff $ Die Normalengleichung lautet: $ E_3: \begin{bmatrix} \vec{x}- \begin{pmatrix} 5\\4\\0 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} -10\\32\\2 \end{pmatrix} =0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Multipliziere\: aus $
$\qquad$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} -10\\32\\2 \end{pmatrix} = -10x+32y+2z $
$\qquad$ $ \begin{pmatrix} 5\\4\\0 \end{pmatrix} \cdot \begin{pmatrix} -10\\32\\2 \end{pmatrix} = 5\cdot (-10)+4\cdot 32+0\cdot 2 =78 $
$\qquad$ Setzte zusammen:
$\qquad \iff $ Die Koordinatenform lautet: $ E_3: -10x+32y+2z=78 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Lies\: den\: Normalenvektor\: n_{E_3}\: der\: Ebene\: $
$\qquad$ $ \vec{n_{E_3}}= \begin{pmatrix} -10\\32\\2 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $E_3:-10x+32y+2z-78=0$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d\: mit\: der\: Hesseschen\: Normalenform $
$\qquad$ $ h=d_D= \begin{vmatrix} \frac {-10\cdot 4+32\cdot (-1)+2\cdot 1-78} { \begin{vmatrix} \begin{pmatrix} -10\\32\\2 \end{pmatrix} \end{vmatrix} } \end{vmatrix} $ = 4,4067
$\:\:\:$ Der Abstand $d$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_D\approx4,41 \: LE $
$c) $ Höhe von $A$ über $BCD:\:\: E_3:\vec{x}= \overrightarrow{OB}+r\cdot \overrightarrow{BC}+s\cdot \overrightarrow{CD}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Parameterform\: von\: E_3 $
$\qquad$ $ E_3: \vec{x}= \begin{pmatrix} 5\\4\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -1-5\\2-4\\2-0 \end{pmatrix} + s\cdot \begin{pmatrix} 3-5\\3-4\\6-0 \end{pmatrix} = \underline{ \begin{pmatrix} 5\\4\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -6\\-2\\2 \end{pmatrix} + s\cdot \begin{pmatrix} -2\\-1\\6 \end{pmatrix} } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Koordinatenform\: von\: E_3 $
$\qquad$ Kreuzprodukt der Richtungsvektoren:
$\qquad$ $ d= \begin{pmatrix} -6\\-2\\2 \end{pmatrix} \times \begin{pmatrix} -2\\-1\\6 \end{pmatrix} = \begin{pmatrix} (-2)\cdot 6-2\cdot (-1)\\ 2\cdot (-2)-(-6)\cdot 6\\ (-6)\cdot (-1)-(-2)\cdot (-2) \end{pmatrix} = \begin{pmatrix} -10\\32\\2 \end{pmatrix} $
$\qquad$ Der Ortsvektor: $\vec{a}= \begin{pmatrix} 5\\4\\0 \end{pmatrix} $
$\qquad \iff $ Die Normalengleichung lautet: $ E_3: \begin{bmatrix} \vec{x}- \begin{pmatrix} 5\\4\\0 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} -10\\32\\2 \end{pmatrix} =0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Multipliziere\: aus $
$\qquad$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} -10\\32\\2 \end{pmatrix} = -10x+32y+2z $
$\qquad$ $ \begin{pmatrix} 5\\4\\0 \end{pmatrix} \cdot \begin{pmatrix} -10\\32\\2 \end{pmatrix} = 5\cdot (-10)+4\cdot 32+0\cdot 2 =78 $
$\qquad$ Setzte zusammen:
$\qquad \iff $ Die Koordinatenform lautet: $ E_3: -10x+32y+2z=78 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Lies\: den\: Normalenvektor\: n_{E_3}\: der\: Ebene\: $
$\qquad$ $ \vec{n_{E_3}}= \begin{pmatrix} -10\\32\\2 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebenengleichung\: um $
$\qquad$ $E_3:-10x+32y+2z-78=0$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: d\: mit\: der\: Hesseschen\: Normalenform $
$\qquad$ $ h=d_D= \begin{vmatrix} \frac {-10\cdot 4+32\cdot (-1)+2\cdot 1-78} { \begin{vmatrix} \begin{pmatrix} -10\\32\\2 \end{pmatrix} \end{vmatrix} } \end{vmatrix} $ = 4,4067
$\:\:\:$ Der Abstand $d$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d_D\approx4,41 \: LE $
Vektorrechnung - Pyramide
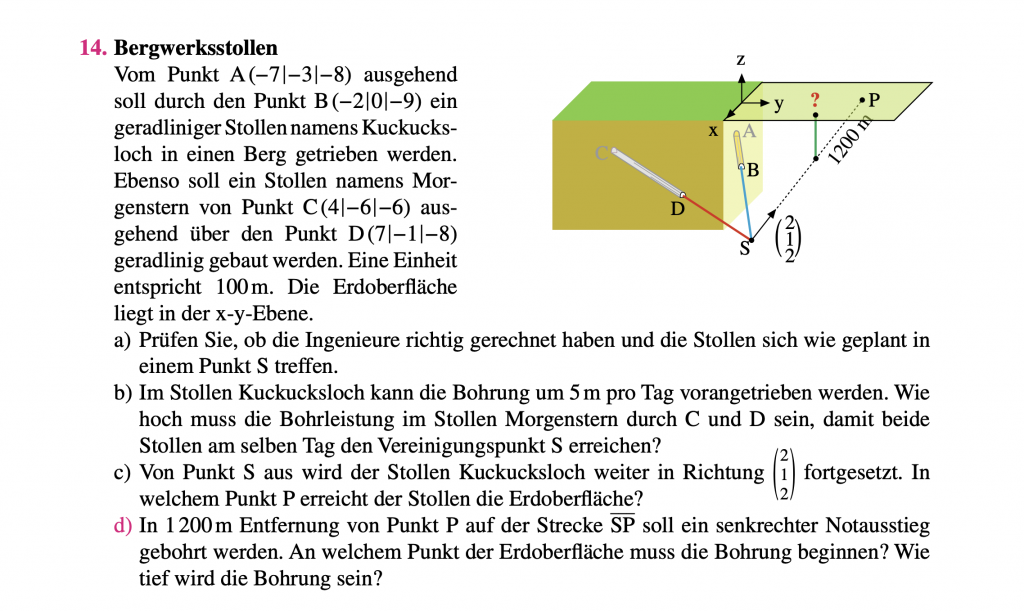
Maths-High-School-6-1
Lösung
Lies die Punkte ab:
$ A \begin{pmatrix} 0\\0\\0 \end{pmatrix} , $ $\:\:$ $ B \begin{pmatrix} 0\\100\\0 \end{pmatrix} , $ $\:\:$ $ C \begin{pmatrix} -100\\100\\0 \end{pmatrix} , $ $\:\:$ $ D \begin{pmatrix} -100\\0\\0 \end{pmatrix} , $ $\:\:$ $ S \begin{pmatrix} -50\\50\\50 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize a)\: Bestimme\: die\: Gleichungen\: der\: Geraden\: der\: vier\: Pyramidenkanten $
$ \:\:\:\:\:\: $ Gerade $ AS \longrightarrow g: \vec{x}= \begin{pmatrix} 0\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -50-0\\50-0\\50-0 \end{pmatrix} = \begin{pmatrix} 0\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -50\\50\\50 \end{pmatrix} $
$ \:\:\:\:\:\: $ Gerade $ BS \longrightarrow h: \vec{x}= \begin{pmatrix} 0\\100\\0 \end{pmatrix} + s\cdot \begin{pmatrix} -50-0\\50-100\\50-0 \end{pmatrix} = \begin{pmatrix} 0\\100\\0 \end{pmatrix} + s\cdot \begin{pmatrix} -50\\-50\\50 \end{pmatrix} $
$ \:\:\:\:\:\: $ Gerade $ CS \longrightarrow i: \vec{x}= \begin{pmatrix} -100\\100\\0 \end{pmatrix} + t\cdot \begin{pmatrix} -50+100\\50-100\\50-0 \end{pmatrix} = \begin{pmatrix} -100\\100\\0 \end{pmatrix} + t\cdot \begin{pmatrix} 50\\-50\\50 \end{pmatrix} $
$ \:\:\:\:\:\: $ Gerade $ DS \longrightarrow j: \vec{x}= \begin{pmatrix} -100\\0\\0 \end{pmatrix} + u\cdot \begin{pmatrix} -50+100\\50-0\\50-0 \end{pmatrix} = \begin{pmatrix} -100\\0\\0 \end{pmatrix} + u\cdot \begin{pmatrix} 50\\50\\50 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b)\: Bestimme\: P $
$ \:\:\:\:\:\: $ Mit $z=10m\: \longrightarrow\: P \begin{pmatrix} x\\y\\10 \end{pmatrix} , $ da sind nur noch $x$ und $y$ zu bestimmen.
$ \:\:\:\:\:\: $ $P$ ist den Schnittpunkt zwischen den Geraden $AP$ und $BS$
$ \:\:\:\:\:\: $ $ \iff \begin{pmatrix} 0\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} x-0\\y-0\\10-0 \end{pmatrix} = \begin{pmatrix} 0\\100\\0 \end{pmatrix} + s\cdot \begin{pmatrix} -50\\-50\\50 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Schreibe\: als\: Lineares\: Gleichungssystem\: (LGS) $
$ \:\:\:\:\:\: $ $ \:\:\:\:\: $ $ \begin{cases} 0 &+ &x \cdot r &= 0 &- &50 \cdot s \:\:\:\: (I)\\ 0 &+ &y \cdot r &= 100 &- &50 \cdot s \:\:\:\: (II)\\ 0 &+ &10 \cdot r &= 0 &+ &50 \cdot s \:\:\:\: (III) \end{cases} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Setzte\: (III)\: in\: (I)\: ein $
$ \:\:\:\:\:\: $ $ \:\:\:\:\: $ $ \Longrightarrow\:\: x\cdot r=-10\cdot r \qquad |\: :r \qquad \longrightarrow \underline{x=-10} $
$ \:\:\:\:\:\: $ $ \:\:\:\:\: $ Für $x=-10$, $r=1$ und $s=\frac{1}{5}=0.2$
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Setzte\: r\: und\: s\: in\: (II)\: ein $
$ \:\:\:\:\:\: $ $ \:\:\:\:\: $ $ \Longrightarrow\:\: y\cdot 1=100-50\cdot \frac{1}{5} \qquad \longrightarrow \underline{y=90} $
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large P \begin{pmatrix} -10\\90\\10 \end{pmatrix} $
$ \:\:\:\: $ $ \qquad $ Gleichung der Geraden $AP$: $\overrightarrow{AP}= \begin{pmatrix} 0\\0\\0 \end{pmatrix} +r \cdot \begin{pmatrix} -10-0\\90-0\\10-0 \end{pmatrix} = \begin{pmatrix} 0\\0\\0 \end{pmatrix} +r \cdot \begin{pmatrix} -10\\90\\10 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Bilde\: die\: Steigung\: von\: P:\: (Sinus\: des\: Steigungswinkels) $
$ \:\:\:\:\:\: $ $ \qquad $ $m_P= \large \frac { \begin{vmatrix} \begin{pmatrix} -10\\90\\10 \end{pmatrix} \cdot \begin{pmatrix} 0\\0\\1 \end{pmatrix} \end{vmatrix} } { \begin{vmatrix} \begin{pmatrix} -10\\90\\10 \end{pmatrix} \end{vmatrix} \cdot \begin{vmatrix} \begin{pmatrix} 0\\0\\1 \end{pmatrix} \end{vmatrix} } =\frac{\sqrt{83}}{83} =0,1097 $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize c)\: Bestimme\: die\: Gleichung\: der\: entsprechenden\: Geraden\: PQ\: $
$ \:\:\:\:\:\: $ $ \qquad $ Bilde die Differenz von P, da P auf PQ liegt
$ \:\:\:\:\:\: $ $ \qquad $ $ PQ= \begin{pmatrix} -100\\100\\0 \end{pmatrix} +r \cdot \begin{pmatrix} 50\\-50\\50 \end{pmatrix} – \begin{pmatrix} -10\\90\\10 \end{pmatrix} = \begin{pmatrix} 50r-90\\-50r+10\\50r-10 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize c)\: Bestimme\: die\: Gleichung\: der\: entsprechenden\: Geraden\: PQ\: $
$ \:\:\:\:\:\: $ $ \qquad $ Bilde die Differenz von P, da P auf PQ liegt
$ \:\:\:\:\:\: $ $ \qquad $ Steigung von $PQ=AP=\frac{\sqrt{83}}{83}$
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: die\: Gleichung\: von\: Q $
$ \:\:\:\:\:\: $ $ \qquad $ $ m_Q=\frac { \large \begin{vmatrix} \begin{pmatrix} 50r-90\\-50r+10\\50r-10 \end{pmatrix} \cdot \begin{pmatrix} 0\\0\\1 \end{pmatrix} \end{vmatrix} } { \begin{vmatrix} \begin{pmatrix} 50r-90\\-50r+10\\50r-10 \end{pmatrix} \end{vmatrix} \cdot \begin{vmatrix} \begin{pmatrix} 0\\0\\1 \end{pmatrix} \end{vmatrix} } = \large \frac{\sqrt{83}}{83} $
$ \large \iff $ $ \large \frac { (50r-10)\cdot 1 } { (\sqrt{(50r-90)^2+(-50r+10)^2+(50r-10)^2}) \: \cdot \: (\sqrt{1^2}) } $
$ \large \iff $ $ \large \frac { 50r-10 } { (\sqrt{(50r-90)^2+(-50r+10)^2+(50r-10)^2}) \: \cdot \: 1 } = \frac{\sqrt{83}}{83} $
$ \large \iff $ $ 83\cdot (50r-10)=\sqrt{83}\cdot (\sqrt{(50r-90)^2+(-50r+10)^2+(50r-10)^2}) \: \cdot \: (1) $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: nach\: r $
$ \:\:\:\:\:\: $ $ \qquad $ $ 8000r\cdot (25r-9)=0\: \longrightarrow\: \begin{cases} r=0\\r=\frac{9}{25}=0,36 \end{cases} $
$ \:\:\:\:\:\: $ $ \qquad $ $ Q= \begin{pmatrix} -100\\100\\0 \end{pmatrix} + 0,36 \cdot \begin{pmatrix} 50\\-50\\50 \end{pmatrix} = \begin{pmatrix} -82\\82\\18 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ $ \iff\: $ Im Punkt $Q \begin{pmatrix} -82\\82\\18 \end{pmatrix} $ endet die Rampe.
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize In\: welchem\: Punkt\: erreicht\: die\: Rampe\: die\: Höhe\: von\: 15m? $
$ \:\:\:\:\:\: $ $ \qquad\: $ Setzte:
$ \:\:\:\:\:\: $ $ \qquad $ $ \begin{pmatrix} -10\\90\\10 \end{pmatrix} +r \cdot \begin{bmatrix} \begin{pmatrix} -82\\82\\18 \end{pmatrix} – \begin{pmatrix} -10\\90\\10 \end{pmatrix} \end{bmatrix} = \begin{pmatrix} x\\y\\15 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow\: x=-55\:\: |\:\: y=85\:\: |\:\: r=0,625 $
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow $ Im Punkt $ \begin{pmatrix} -55\\85\\15 \end{pmatrix} $ erreicht die Rampe die Höhe von $15m.$
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize In\: welchen\: Punkte\: durchstoßen\: die\: Pyramidenkanten\: eine\: Höhe\: von\: 20m? $
$ \:\:\:\:\:\: $ $ \qquad $ Stelle die Geradengleichung für $AS$:
$ \:\:\:\:\:\: $ $ \qquad $ $AS:\vec{x}=$ $ \begin{pmatrix} 0\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -50\\50\\50 \end{pmatrix} = \begin{pmatrix} x\\y\\20 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ $ \iff $ $ \begin{cases} -50r=x\\ 50r=y\\ 50r=20 \qquad |\: r=\frac{2}{5}=0,4 \:\:|\:\: -50\cdot \frac{2}{5}=-20=x \:\:|\:\: 50\cdot \frac{2}{5}=20=y \end{cases} $
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow AS = \begin{pmatrix} -20\\20\\20 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ Stelle die Geradengleichung für $BS$:
$ \:\:\:\:\:\: $ $ \qquad $ $AS:\vec{x}=$ $ \begin{pmatrix} 0\\100\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -50\\-50\\50 \end{pmatrix} = \begin{pmatrix} x\\y\\20 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ $ \iff $ $ \begin{cases} -50s &=x\\ 100-50s &=y\\ 50s &=20 \end{cases} $
$ \:\:\:\:\:\: $ $ \qquad\qquad $ $ \qquad |\: s=\frac{2}{5}=0,4 \:\:|\:\: -50\cdot \frac{2}{5}=-20=x \:\:|\:\: 100-50\cdot \frac{2}{5}=20=y $
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow BS = \begin{pmatrix} -20\\80\\20 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ Stelle die Geradengleichung für $CS$ und $DS$: Gleiches Verfahren
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow CS = \begin{pmatrix} -80\\80\\20 \end{pmatrix} $ $ \:\:\: $ und $ \:\:\: $ $ DS= \begin{pmatrix} -80\\20\\20 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize In\: welcher\: Höhe\: beträgt\: der\: horizontale\: Querschnitt\: der\: Pyramide\: 25m²? $
$ \:\:\:\:\:\: $ $ \qquad $ Da $A=a\cdot a=25m^2 \longrightarrow$ Grundseitenlänge $a=5m$
$ \:\:\:\:\:\: $ $ \qquad\qquad $ Mit dem Strahlensatz: $\frac{h_1}{5}=\frac{50}{100} \longrightarrow h_1=2,5m$
$ \:\:\:\:\:\: $ $ \qquad\qquad $ Also, $50m-2,5m=47,5m$
$ \:\:\:\:\:\: $ $ \qquad $ $ \longrightarrow$ In Höher $47,5m$ beträgt der horizontale Querschnitt der Pyramide $25m². $
$ \:\:\:\:\:\: $ $ \qquad $ Vom Punkt $T \begin{pmatrix} 50\\-50\\100 \end{pmatrix} $ fällt Licht in Richtung $ \begin{pmatrix} -1-a\\3-a\\a-2 \end{pmatrix} .$
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize \textcolor{red}{e)} \: Zeige,\: dass\: vom\: Punkt\: T\: je\: ein\: Lichtstrahl\: auf\: die\: Punkte\: B\: und\: S\: fällt. $
$ \:\:\:\:\:\: $ $ \qquad $ Prüfe ob $B$ auf $T$ liegt:
$ \:\:\:\:\:\: $ $ \qquad $ Setzte: $ \begin{pmatrix} 0\\100\\0 \end{pmatrix} = \begin{pmatrix} 50\\-50\\100 \end{pmatrix} + r\cdot \begin{pmatrix} -1-a\\3-a\\a-2 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: in\: Lineares\: Gleichungssystem\: um\: (LGS) $
$ \:\:\:\:\:\: $ $ \qquad $ $ \begin{cases} 0 &= 50-r-ar \qquad\:\:\:\:\:\:\: (I)\\ 100 &= -50+3r-ar \qquad (II)\\ 0 &= 100-2r+ar \qquad (III) \end{cases} $
$ \:\:\:\:\:\: $ $ \qquad $ $(I)+(III): 0=150-3r \: \longrightarrow r=50$
$ \:\:\:\:\:\: $ $ \qquad $ Setzte $r=50$ in (II) ein
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow \:\: 100=-50+3(50)-a(50) $
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow \:\: 0=-50a \:\: \longrightarrow a=0 $
$ \:\:\:\:\:\: $ $ \qquad $ Setzte $r$ und $a$ in $ \: \begin{pmatrix} 50\\-50\\100 \end{pmatrix} + 50\cdot \begin{pmatrix} -1-0\\3-0\\0-2 \end{pmatrix} = \begin{pmatrix} 0\\100\\0 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ Für $r=50$ und $a=0$ liegt $B$ auf $T.$
$ \:\:\:\:\:\: $ $ \qquad $ Prüfe ob $S$ auf $T$ liegt:
$ \:\:\:\:\:\: $ $ \qquad $ Setzte: $ \begin{pmatrix} -50\\50\\50 \end{pmatrix} = \begin{pmatrix} 50\\-50\\100 \end{pmatrix} + r\cdot \begin{pmatrix} -1-a\\3-a\\a-2 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: in\: Lineares\: Gleichungssystem\: um\: (LGS) $
$ \:\:\:\:\:\: $ $ \qquad $ $ \begin{cases} -50 &= 50-r-ar \qquad\:\:\:\:\:\:\: (I)\\ 50 &= -50+3r-ar \qquad (II)\\ 50 &= 100-2r+ar \qquad (III) \end{cases} $
$ \:\:\:\:\:\: $ $ \qquad $ $(I)-(II): -200=-4r \: \longrightarrow r=50$
$ \:\:\:\:\:\: $ $ \qquad $ Setzte $r=50$ in (III) ein
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow \:\: -50=-2(50)-50a $
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow \:\: 50=-50a \:\: \longrightarrow a=-1 $
$ \:\:\:\:\:\: $ $ \qquad $ Setzte $r$ und $a$ in $ \: \begin{pmatrix} 50\\-50\\100 \end{pmatrix} + 50\cdot \begin{pmatrix} -1+1\\3+1\\-1-2 \end{pmatrix} = \begin{pmatrix} 0\\150\\-50 \end{pmatrix} $
$ A \begin{pmatrix} 0\\0\\0 \end{pmatrix} , $ $\:\:$ $ B \begin{pmatrix} 0\\100\\0 \end{pmatrix} , $ $\:\:$ $ C \begin{pmatrix} -100\\100\\0 \end{pmatrix} , $ $\:\:$ $ D \begin{pmatrix} -100\\0\\0 \end{pmatrix} , $ $\:\:$ $ S \begin{pmatrix} -50\\50\\50 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize a)\: Bestimme\: die\: Gleichungen\: der\: Geraden\: der\: vier\: Pyramidenkanten $
$ \:\:\:\:\:\: $ Gerade $ AS \longrightarrow g: \vec{x}= \begin{pmatrix} 0\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -50-0\\50-0\\50-0 \end{pmatrix} = \begin{pmatrix} 0\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -50\\50\\50 \end{pmatrix} $
$ \:\:\:\:\:\: $ Gerade $ BS \longrightarrow h: \vec{x}= \begin{pmatrix} 0\\100\\0 \end{pmatrix} + s\cdot \begin{pmatrix} -50-0\\50-100\\50-0 \end{pmatrix} = \begin{pmatrix} 0\\100\\0 \end{pmatrix} + s\cdot \begin{pmatrix} -50\\-50\\50 \end{pmatrix} $
$ \:\:\:\:\:\: $ Gerade $ CS \longrightarrow i: \vec{x}= \begin{pmatrix} -100\\100\\0 \end{pmatrix} + t\cdot \begin{pmatrix} -50+100\\50-100\\50-0 \end{pmatrix} = \begin{pmatrix} -100\\100\\0 \end{pmatrix} + t\cdot \begin{pmatrix} 50\\-50\\50 \end{pmatrix} $
$ \:\:\:\:\:\: $ Gerade $ DS \longrightarrow j: \vec{x}= \begin{pmatrix} -100\\0\\0 \end{pmatrix} + u\cdot \begin{pmatrix} -50+100\\50-0\\50-0 \end{pmatrix} = \begin{pmatrix} -100\\0\\0 \end{pmatrix} + u\cdot \begin{pmatrix} 50\\50\\50 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b)\: Bestimme\: P $
$ \:\:\:\:\:\: $ Mit $z=10m\: \longrightarrow\: P \begin{pmatrix} x\\y\\10 \end{pmatrix} , $ da sind nur noch $x$ und $y$ zu bestimmen.
$ \:\:\:\:\:\: $ $P$ ist den Schnittpunkt zwischen den Geraden $AP$ und $BS$
$ \:\:\:\:\:\: $ $ \iff \begin{pmatrix} 0\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} x-0\\y-0\\10-0 \end{pmatrix} = \begin{pmatrix} 0\\100\\0 \end{pmatrix} + s\cdot \begin{pmatrix} -50\\-50\\50 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Schreibe\: als\: Lineares\: Gleichungssystem\: (LGS) $
$ \:\:\:\:\:\: $ $ \:\:\:\:\: $ $ \begin{cases} 0 &+ &x \cdot r &= 0 &- &50 \cdot s \:\:\:\: (I)\\ 0 &+ &y \cdot r &= 100 &- &50 \cdot s \:\:\:\: (II)\\ 0 &+ &10 \cdot r &= 0 &+ &50 \cdot s \:\:\:\: (III) \end{cases} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Setzte\: (III)\: in\: (I)\: ein $
$ \:\:\:\:\:\: $ $ \:\:\:\:\: $ $ \Longrightarrow\:\: x\cdot r=-10\cdot r \qquad |\: :r \qquad \longrightarrow \underline{x=-10} $
$ \:\:\:\:\:\: $ $ \:\:\:\:\: $ Für $x=-10$, $r=1$ und $s=\frac{1}{5}=0.2$
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Setzte\: r\: und\: s\: in\: (II)\: ein $
$ \:\:\:\:\:\: $ $ \:\:\:\:\: $ $ \Longrightarrow\:\: y\cdot 1=100-50\cdot \frac{1}{5} \qquad \longrightarrow \underline{y=90} $
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large P \begin{pmatrix} -10\\90\\10 \end{pmatrix} $
$ \:\:\:\: $ $ \qquad $ Gleichung der Geraden $AP$: $\overrightarrow{AP}= \begin{pmatrix} 0\\0\\0 \end{pmatrix} +r \cdot \begin{pmatrix} -10-0\\90-0\\10-0 \end{pmatrix} = \begin{pmatrix} 0\\0\\0 \end{pmatrix} +r \cdot \begin{pmatrix} -10\\90\\10 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Bilde\: die\: Steigung\: von\: P:\: (Sinus\: des\: Steigungswinkels) $
$ \:\:\:\:\:\: $ $ \qquad $ $m_P= \large \frac { \begin{vmatrix} \begin{pmatrix} -10\\90\\10 \end{pmatrix} \cdot \begin{pmatrix} 0\\0\\1 \end{pmatrix} \end{vmatrix} } { \begin{vmatrix} \begin{pmatrix} -10\\90\\10 \end{pmatrix} \end{vmatrix} \cdot \begin{vmatrix} \begin{pmatrix} 0\\0\\1 \end{pmatrix} \end{vmatrix} } =\frac{\sqrt{83}}{83} =0,1097 $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize c)\: Bestimme\: die\: Gleichung\: der\: entsprechenden\: Geraden\: PQ\: $
$ \:\:\:\:\:\: $ $ \qquad $ Bilde die Differenz von P, da P auf PQ liegt
$ \:\:\:\:\:\: $ $ \qquad $ $ PQ= \begin{pmatrix} -100\\100\\0 \end{pmatrix} +r \cdot \begin{pmatrix} 50\\-50\\50 \end{pmatrix} – \begin{pmatrix} -10\\90\\10 \end{pmatrix} = \begin{pmatrix} 50r-90\\-50r+10\\50r-10 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize c)\: Bestimme\: die\: Gleichung\: der\: entsprechenden\: Geraden\: PQ\: $
$ \:\:\:\:\:\: $ $ \qquad $ Bilde die Differenz von P, da P auf PQ liegt
$ \:\:\:\:\:\: $ $ \qquad $ Steigung von $PQ=AP=\frac{\sqrt{83}}{83}$
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: die\: Gleichung\: von\: Q $
$ \:\:\:\:\:\: $ $ \qquad $ $ m_Q=\frac { \large \begin{vmatrix} \begin{pmatrix} 50r-90\\-50r+10\\50r-10 \end{pmatrix} \cdot \begin{pmatrix} 0\\0\\1 \end{pmatrix} \end{vmatrix} } { \begin{vmatrix} \begin{pmatrix} 50r-90\\-50r+10\\50r-10 \end{pmatrix} \end{vmatrix} \cdot \begin{vmatrix} \begin{pmatrix} 0\\0\\1 \end{pmatrix} \end{vmatrix} } = \large \frac{\sqrt{83}}{83} $
$ \large \iff $ $ \large \frac { (50r-10)\cdot 1 } { (\sqrt{(50r-90)^2+(-50r+10)^2+(50r-10)^2}) \: \cdot \: (\sqrt{1^2}) } $
$ \large \iff $ $ \large \frac { 50r-10 } { (\sqrt{(50r-90)^2+(-50r+10)^2+(50r-10)^2}) \: \cdot \: 1 } = \frac{\sqrt{83}}{83} $
$ \large \iff $ $ 83\cdot (50r-10)=\sqrt{83}\cdot (\sqrt{(50r-90)^2+(-50r+10)^2+(50r-10)^2}) \: \cdot \: (1) $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: nach\: r $
$ \:\:\:\:\:\: $ $ \qquad $ $ 8000r\cdot (25r-9)=0\: \longrightarrow\: \begin{cases} r=0\\r=\frac{9}{25}=0,36 \end{cases} $
$ \:\:\:\:\:\: $ $ \qquad $ $ Q= \begin{pmatrix} -100\\100\\0 \end{pmatrix} + 0,36 \cdot \begin{pmatrix} 50\\-50\\50 \end{pmatrix} = \begin{pmatrix} -82\\82\\18 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ $ \iff\: $ Im Punkt $Q \begin{pmatrix} -82\\82\\18 \end{pmatrix} $ endet die Rampe.
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize In\: welchem\: Punkt\: erreicht\: die\: Rampe\: die\: Höhe\: von\: 15m? $
$ \:\:\:\:\:\: $ $ \qquad\: $ Setzte:
$ \:\:\:\:\:\: $ $ \qquad $ $ \begin{pmatrix} -10\\90\\10 \end{pmatrix} +r \cdot \begin{bmatrix} \begin{pmatrix} -82\\82\\18 \end{pmatrix} – \begin{pmatrix} -10\\90\\10 \end{pmatrix} \end{bmatrix} = \begin{pmatrix} x\\y\\15 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow\: x=-55\:\: |\:\: y=85\:\: |\:\: r=0,625 $
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow $ Im Punkt $ \begin{pmatrix} -55\\85\\15 \end{pmatrix} $ erreicht die Rampe die Höhe von $15m.$
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize In\: welchen\: Punkte\: durchstoßen\: die\: Pyramidenkanten\: eine\: Höhe\: von\: 20m? $
$ \:\:\:\:\:\: $ $ \qquad $ Stelle die Geradengleichung für $AS$:
$ \:\:\:\:\:\: $ $ \qquad $ $AS:\vec{x}=$ $ \begin{pmatrix} 0\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -50\\50\\50 \end{pmatrix} = \begin{pmatrix} x\\y\\20 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ $ \iff $ $ \begin{cases} -50r=x\\ 50r=y\\ 50r=20 \qquad |\: r=\frac{2}{5}=0,4 \:\:|\:\: -50\cdot \frac{2}{5}=-20=x \:\:|\:\: 50\cdot \frac{2}{5}=20=y \end{cases} $
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow AS = \begin{pmatrix} -20\\20\\20 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ Stelle die Geradengleichung für $BS$:
$ \:\:\:\:\:\: $ $ \qquad $ $AS:\vec{x}=$ $ \begin{pmatrix} 0\\100\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -50\\-50\\50 \end{pmatrix} = \begin{pmatrix} x\\y\\20 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ $ \iff $ $ \begin{cases} -50s &=x\\ 100-50s &=y\\ 50s &=20 \end{cases} $
$ \:\:\:\:\:\: $ $ \qquad\qquad $ $ \qquad |\: s=\frac{2}{5}=0,4 \:\:|\:\: -50\cdot \frac{2}{5}=-20=x \:\:|\:\: 100-50\cdot \frac{2}{5}=20=y $
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow BS = \begin{pmatrix} -20\\80\\20 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ Stelle die Geradengleichung für $CS$ und $DS$: Gleiches Verfahren
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow CS = \begin{pmatrix} -80\\80\\20 \end{pmatrix} $ $ \:\:\: $ und $ \:\:\: $ $ DS= \begin{pmatrix} -80\\20\\20 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize In\: welcher\: Höhe\: beträgt\: der\: horizontale\: Querschnitt\: der\: Pyramide\: 25m²? $
$ \:\:\:\:\:\: $ $ \qquad $ Da $A=a\cdot a=25m^2 \longrightarrow$ Grundseitenlänge $a=5m$
$ \:\:\:\:\:\: $ $ \qquad\qquad $ Mit dem Strahlensatz: $\frac{h_1}{5}=\frac{50}{100} \longrightarrow h_1=2,5m$
$ \:\:\:\:\:\: $ $ \qquad\qquad $ Also, $50m-2,5m=47,5m$
$ \:\:\:\:\:\: $ $ \qquad $ $ \longrightarrow$ In Höher $47,5m$ beträgt der horizontale Querschnitt der Pyramide $25m². $
$ \:\:\:\:\:\: $ $ \qquad $ Vom Punkt $T \begin{pmatrix} 50\\-50\\100 \end{pmatrix} $ fällt Licht in Richtung $ \begin{pmatrix} -1-a\\3-a\\a-2 \end{pmatrix} .$
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize \textcolor{red}{e)} \: Zeige,\: dass\: vom\: Punkt\: T\: je\: ein\: Lichtstrahl\: auf\: die\: Punkte\: B\: und\: S\: fällt. $
$ \:\:\:\:\:\: $ $ \qquad $ Prüfe ob $B$ auf $T$ liegt:
$ \:\:\:\:\:\: $ $ \qquad $ Setzte: $ \begin{pmatrix} 0\\100\\0 \end{pmatrix} = \begin{pmatrix} 50\\-50\\100 \end{pmatrix} + r\cdot \begin{pmatrix} -1-a\\3-a\\a-2 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: in\: Lineares\: Gleichungssystem\: um\: (LGS) $
$ \:\:\:\:\:\: $ $ \qquad $ $ \begin{cases} 0 &= 50-r-ar \qquad\:\:\:\:\:\:\: (I)\\ 100 &= -50+3r-ar \qquad (II)\\ 0 &= 100-2r+ar \qquad (III) \end{cases} $
$ \:\:\:\:\:\: $ $ \qquad $ $(I)+(III): 0=150-3r \: \longrightarrow r=50$
$ \:\:\:\:\:\: $ $ \qquad $ Setzte $r=50$ in (II) ein
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow \:\: 100=-50+3(50)-a(50) $
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow \:\: 0=-50a \:\: \longrightarrow a=0 $
$ \:\:\:\:\:\: $ $ \qquad $ Setzte $r$ und $a$ in $ \: \begin{pmatrix} 50\\-50\\100 \end{pmatrix} + 50\cdot \begin{pmatrix} -1-0\\3-0\\0-2 \end{pmatrix} = \begin{pmatrix} 0\\100\\0 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \qquad $ Für $r=50$ und $a=0$ liegt $B$ auf $T.$
$ \:\:\:\:\:\: $ $ \qquad $ Prüfe ob $S$ auf $T$ liegt:
$ \:\:\:\:\:\: $ $ \qquad $ Setzte: $ \begin{pmatrix} -50\\50\\50 \end{pmatrix} = \begin{pmatrix} 50\\-50\\100 \end{pmatrix} + r\cdot \begin{pmatrix} -1-a\\3-a\\a-2 \end{pmatrix} $
$ \:\:\:\:\:\: $ $ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: in\: Lineares\: Gleichungssystem\: um\: (LGS) $
$ \:\:\:\:\:\: $ $ \qquad $ $ \begin{cases} -50 &= 50-r-ar \qquad\:\:\:\:\:\:\: (I)\\ 50 &= -50+3r-ar \qquad (II)\\ 50 &= 100-2r+ar \qquad (III) \end{cases} $
$ \:\:\:\:\:\: $ $ \qquad $ $(I)-(II): -200=-4r \: \longrightarrow r=50$
$ \:\:\:\:\:\: $ $ \qquad $ Setzte $r=50$ in (III) ein
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow \:\: -50=-2(50)-50a $
$ \:\:\:\:\:\: $ $ \qquad $ $ \Longrightarrow \:\: 50=-50a \:\: \longrightarrow a=-1 $
$ \:\:\:\:\:\: $ $ \qquad $ Setzte $r$ und $a$ in $ \: \begin{pmatrix} 50\\-50\\100 \end{pmatrix} + 50\cdot \begin{pmatrix} -1+1\\3+1\\-1-2 \end{pmatrix} = \begin{pmatrix} 0\\150\\-50 \end{pmatrix} $
Winkel und Abstände II
II- Abstände – Lotfußpunktverfahren
Der Abstand eines Punktes P von einer Geraden $g$ ist gleich dem Betrag des Vektors $\overrightarrow{PF}$, wobei $F$ der Fußpunkt des Lotes von $P$ auf $g$ ist.
Berechnung
Die Berechnung des Abstandes erfolgt in drei Schritten:
- Aufstellen der Gleichung einer Hilfsebene $E,$ die durch $P$ geht und zu $g$ orthogonal ist,
- Berechnung des Schnittpunktes $F$ von $E$ und $g,$
- Berechnung des Betrages von $\overrightarrow{PF}.$
Beispielaufgaben
Berechne jeweils den Abstand des Punktes $P$ von der Geraden $g.$
-
$
P\begin{pmatrix}-2\\2\\1
\end{pmatrix},
\:\:
g:\vec{x}
=
\begin{pmatrix}
1\\3\\-1
\end{pmatrix}
+r
\begin{pmatrix}
0\\2\\1
\end{pmatrix}
$
Lösung$ P\begin{pmatrix}-2\\2\\1 \end{pmatrix}, \:\: g:\vec{x} = \begin{pmatrix} 1\\3\\-1 \end{pmatrix} +r \begin{pmatrix} 0\\2\\1 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize F\: liegt\: auf\: der\: Geraden\: g,\: vektoriell\: ausgedrückt: $
$ \:\:\:\:\:\: $ $\overrightarrow{OF}$ $=$ $ \begin{pmatrix} 1 &+ &0 \cdot r\\ 3 &+ &2 \cdot r\\ -1 &+ &1 \cdot r \end{pmatrix} $
$ \qquad $ und den Vektor von $F$ nach $P:$
$ \:\:\:\:\:\: $ $\overrightarrow{FP}=P-F$ $=$ $ \begin{pmatrix} -2 &- &(1+0\cdot r)\\ 2 &- &(3+2\cdot r)\\ 1 &- &((-1)+1\cdot r) \end{pmatrix} = \begin{pmatrix} -3\\-1-2r\\2-r \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Setzte\: Richtungsvektor\: von\: g\: orthogonal\: zum\: Vektor\: \overrightarrow{FP}: $
$ \:\:\:\:\:\: $ $ \Longrightarrow g \perp \overrightarrow{FP} \: \iff \: \begin{pmatrix} 0\\2\\1 \end{pmatrix} \cdot \begin{pmatrix} -3\\-1-2r\\2-r \end{pmatrix} =0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: das\: Skakarprodukt $
$ \:\:\:\:\:\: $ $ \begin{pmatrix} 0\\2\\1 \end{pmatrix} \cdot \begin{pmatrix} -3\\-1-2r\\2-r \end{pmatrix} =0 $
$ \qquad\qquad\qquad\qquad\:\:\:\:\: \iff $ $ 0\cdot (-3)+2\cdot (-1-2r)+1\cdot(2-r)=0 $
$ \qquad\qquad\qquad\qquad\:\:\:\:\: \iff $ $ -5r=0\:\: \longrightarrow\:\: r=0\:\: (Geradenparameter) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Setzte\: r\: in\: \overrightarrow{OF}\: ein $
$ \:\:\:\:\:\:\:\: $ $ \overrightarrow{OF} = \begin{pmatrix} 1 &+ &0\cdot 0\\ 3 &+ &2\cdot 0\\ -1 &+ &1\cdot 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \\ -1 \end{pmatrix} \:\: (Lotfußpunkt\: F) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Setzte\: r\: in\: \overrightarrow{FP}\: ein $
$ \:\:\:\:\:\:\:\: $ $ \overrightarrow{OF} = \begin{pmatrix} -3\\ -1-2\cdot 0\\ 2-0 \end{pmatrix} = \begin{pmatrix} -3 \\ -1 \\ 2 \end{pmatrix} \:\: (Vektor\: FP) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Abstand\: von\: g\: zu\: P $
$ \:\:\:\:\:\:\:\: $ $ d(g,P)=\sqrt{(-3)^2+(-1)^2+2^2}\approx3,74165 $
Der Abstand des Punktes $P$ von der Geraden $g$ lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large |\overrightarrow{PF}|\approx3,42\: LE $ -
$
P\begin{pmatrix}
3\\5\\2
\end{pmatrix},
\:\:
g:\vec{x}
=
\begin{pmatrix}
-2\\-3\\4
\end{pmatrix}
+r
\begin{pmatrix}
1\\-1\\3
\end{pmatrix}
$
$\:\:$$|\overrightarrow{PF}|\approx9,30\: LE$ -
$
P\begin{pmatrix}
3\\2\\-1
\end{pmatrix},
\:\:
g:\vec{x}
=
\begin{pmatrix}
1\\2\\3
\end{pmatrix}
+r
\begin{pmatrix}
2\\4\\2
\end{pmatrix}
$
$\:\:$$|\overrightarrow{PF}|\approx4,45\: LE$
$\:\:\:$Unter dem Abstand $d$ eines Punktes P von einer Ebene $E$ versteht man die Länge des Lotes
$\:\:\:$von $P$ auf die Ebene, also die Länge der Strecke von $P$ bis zum Fußpunkt $F$ des Lotes.
Berechnung
Die Berechnung des Abstandes erfolgt in drei Schritten:
- Aufstellen der zu $E$ orthogonalen Lotgerade $g$ durch $P,$
- Berechnung des Schnittpunktes $F$ von $g$ und $E,$
- Berechnung des Betrags des Vektor $\overrightarrow{PF}.$
Tipp
Beispielaufgaben
-
Bestimme den Abstand des Punktes $P\begin{pmatrix}2\\4\\1\end{pmatrix}$ von der Ebene $E:3x-2y+2z=3.$
Lösung
$ P \begin{pmatrix} 2\\4\\1 \end{pmatrix} $ $\:\:$ und $\:\:$ $ E: 3x-2y+2z=3 $ $ \longrightarrow n_E \begin{pmatrix} 3\\-2\\2 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: eine\: Hilfsgerade/Lotgerade\: mit\: P\: und\: n_E $
$ h:\vec{x} = \begin{pmatrix} 2\\4\\1 \end{pmatrix} + t\cdot \begin{pmatrix} 3\\-2\\2 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Schnittpunkt\: Lotgeraden\: mit\: der\: Ebene \: E $
$ \qquad $ $ 3(2+3t)-2(4-2t)+2(1+2t)=3 $
$ \qquad $ $ \iff 6+9t-8+4t+2+4t=3 $
$ \qquad $ $ \iff 17t=3 \longrightarrow t=\frac{3}{17} \approx0,1765 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Koordinaten\: des\: Lotfußpunkts:\: Setzte\: t\: in\: Lotgerade\: ein $
$ \vec{f} = \begin{pmatrix} 2\\4\\1 \end{pmatrix} + 0,1765\cdot \begin{pmatrix} 3\\-2\\2 \end{pmatrix} = \begin{pmatrix} 2+0,1765 \cdot 3\\ 4+0,1765 \cdot (-2)\\ 1+0,1765 \cdot 2 \end{pmatrix} $ $ \longrightarrow \vec{f}= \begin{pmatrix} 2,529\\ 3,647\\ 1,352 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Vektor\:$ $\overrightarrow{PF}$
$ \overrightarrow{PF} = \vec{f}- \vec{P} = \begin{pmatrix} 2,529-2\\ 3,647-4\\ 1,353-1 \end{pmatrix} \longrightarrow \overrightarrow{PF} = \begin{pmatrix} 0.529\\ -1,647\\ 0,353 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: der\: Abstand $
$ d=|\overrightarrow{PF}| = \sqrt{(2,529-2)^2+(3,647-4)^2+(1,353-1)^2}=0,7273 $
Der Abstand zwischen $P$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d \approx0.73 \: LE $ -
Gesucht ist der Abstand des Punktes
$P
\begin{pmatrix}
5\\8\\9
\end{pmatrix}
$
von der Ebene
$E:
\begin{bmatrix}
\vec{x}-
\begin{pmatrix}
2\\0\\2
\end{pmatrix}
\end{bmatrix}
\cdot
\begin{pmatrix}
2\\3\\4
\end{pmatrix}
=0.
$
Lösung
$P \begin{pmatrix} 5\\8\\9 \end{pmatrix} $ $\:$ und $\:$ $E: \begin{bmatrix} \vec{x}- \begin{pmatrix} 2\\0\\2 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 2\\3\\4 \end{pmatrix} =0 $
$\:\:$ $ \: \Large \Bigg\downarrow $ $ \normalsize Wandle\: die\: Normalenform\: von\: E\: in\: Koordinatenform\: um $
$\qquad$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 2\\3\\4 \end{pmatrix} = 2x+3y+4z $
$\qquad$ $ \begin{pmatrix} 2\\0\\2 \end{pmatrix} \cdot \begin{pmatrix} 2\\3\\4 \end{pmatrix} = 2\cdot 2+0\cdot 3+2\cdot 4=12 $
$\qquad\qquad$ $ \longrightarrow E:2x+3y+4z=12 \:\:\:\: und \:\:\:\: n_E=\begin{pmatrix}2\\3\\4 \end{pmatrix} $
$\:\:$ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: eine\: Hilfsgerade/Lotgerade\: mit\: P\: und\: n_E $
$\qquad$ $ h: \vec{x}= \begin{pmatrix} 5\\8\\9 \end{pmatrix} + t \cdot \begin{pmatrix} 2\\3\\4 \end{pmatrix} $
$\:\:$ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Schnittpunkt\: Lotgeraden\: mit\: der\: Ebene \: E $
$\qquad\qquad$ $ 2(5+2t)+3(8+3t)+4(9+4t)=12 $
$\qquad\qquad$ $ \iff 10+4t+24+9t+36+16t=12 $
$\qquad\qquad$ $ \iff 29t+70=12 \qquad |\: -70 $
$\qquad\qquad$ $ \iff 29t=-58 \qquad\:\:\:\:\:\:\: |\: :29 \:\:\:\: \longrightarrow \:\:\:\: t=-2 $
$\:\:$ $ \: \Large \Bigg\downarrow $ $ \normalsize Koordinaten\: des\: Lotfußpunkts:\: Setzte\: t\: in\: Lotgerade\: ein $
$\qquad$ $ \vec{f}= \begin{pmatrix} 5\\8\\9 \end{pmatrix} + (-2) \cdot \begin{pmatrix} 2\\3\\4 \end{pmatrix} = \begin{pmatrix} 5-4\\8-6\\9-8 \end{pmatrix} $ $ \longrightarrow \vec{f}= \begin{pmatrix} 1\\2\\1 \end{pmatrix} $
$\:\:$ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Vektor\: \overrightarrow{PF} $
$\qquad$ $ \overrightarrow{PF} = \vec{f}- \vec{P} = \begin{pmatrix} 1-5\\2-8\\1-9 \end{pmatrix} $ $\:\:\:\:$ $\longrightarrow$ $\:\:\:\:$ $ \overrightarrow{PF} = \begin{pmatrix} -4\\-6\\-8 \end{pmatrix} $
$\:\:$ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: der\: Abstand\: d $
$\qquad$ $ d=|\overrightarrow{PF}| = \sqrt{(-4)^2+(-6)^2+(-8)^2}=10,770 $
$\:\:\:$ Der Abstand zwischen $P$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d \approx10.77 \: LE $ -
Berechne den Abstand des Punktes $P(10|-1|-4)$ von der Ebene
$E:2x-8y+16z=45$
$\:\:$$F(10,5|-3|0)$ $d=|\overrightarrow{PF}|=4,5\: LE$ -
Gegeben ist die Ebene $E$ durch die Punkte $A(2|4|3),$ $B(-1|5|3)$ und $C(3|2|3).$ Berechne den Abstand des Punktes $P(6|8|7).$
Lösung$A(2|4|3),$ $\:\:B(-1|5|3)\:\:$ und $\:\:C(3|2|3)$ $\:\:\:\:|\:\:\:\:$ $P(6|8|7)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: die\: Ebene\: E\: in\: Parameterform $
$ \qquad $ $ E:\vec{x} = \begin{pmatrix} 2\\4\\3 \end{pmatrix} + r\cdot \begin{pmatrix} -3\\1\\0 \end{pmatrix} + s\cdot \begin{pmatrix} 1\\-2\\0 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Schreibe\: die\: Koordinatenform\: von\: E $
$ \qquad $ Richtungsvektor: $ \vec{a}= \begin{pmatrix} 2\\4\\3 \end{pmatrix} $
$ \qquad $ Normalenvektor:
$ \qquad $ Berechne das Kreuzprodukt der beiden Richtungsvektoren:
$ \qquad $ $ \vec{n}= \begin{pmatrix} -3\\1\\0 \end{pmatrix} \times \begin{pmatrix} 1\\-2\\0 \end{pmatrix} = \begin{pmatrix} 0\cdot 1 &- &0\cdot (-2)\\ 0\cdot 1 &- &0\cdot (-3)\\ (-3)\cdot (-2) &- &1\cdot 1 \end{pmatrix} = \begin{pmatrix} 0\\0\\5 \end{pmatrix} $
$ \qquad $ Die Normalenform lautet: $ E: \begin{bmatrix} \vec{x} – \begin{pmatrix} 2\\4\\3 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 0\\0\\5 \end{pmatrix} =0 $
$ \qquad $ Wandle in Koordinatenform um: Multipliziere aus
$ \qquad $ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 0\\0\\5 \end{pmatrix} =0x+0y+5z $
$ \qquad $ $ \begin{pmatrix} 2\\4\\3 \end{pmatrix} \cdot \begin{pmatrix} 0\\0\\5 \end{pmatrix} =15 $
$ \qquad $ Die Koordinatenform lautet: $0x+0y+5z=15$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Stelle\: eine\: Hilfsgerade/Lotgerade\: mit\: P\: und\: n_E $
$ \qquad $ $ h: \vec{x} = \begin{pmatrix} 6\\8\\7 \end{pmatrix} + t\cdot \begin{pmatrix} 0\\0\\5 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Schnittpunkt\: Lotgeraden\: mit\: der\: Ebene\: E $
$ \qquad \qquad $ $ 5(7+5t)=15 \qquad\:\:\:\:| :5 $
$ \qquad \qquad $ $ \iff 7+5t=3 \qquad | -7 $
$ \qquad \qquad $ $ \iff 5t=-4 \:\:\longrightarrow\:\: t=-\frac{4}{5} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Koordinaten\: des\: Lotfußpunkts:\: Setzte\: t\: in\: Lotgerade\: ein $
$\qquad$ $ \vec{f} = \begin{pmatrix} 6\\8\\7 \end{pmatrix} + (-\frac{4}{5}) \cdot \begin{pmatrix} 0\\0\\5 \end{pmatrix} = \begin{pmatrix} 6+0\\8+0\\7+(-\frac{4}{5}\cdot 5) \end{pmatrix} $ $\longrightarrow \vec{f}= \begin{pmatrix} 6\\8\\3 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Vektor\:$ $\overrightarrow{PF} $
$\qquad$ $ \overrightarrow{PF} = \vec{f}-\vec{P} = \begin{pmatrix} 6-6\\8-8\\3-7 \end{pmatrix} = \begin{pmatrix} 0\\0\\-4 \end{pmatrix} \: \longrightarrow \: \overrightarrow{PF} = \begin{pmatrix} 0\\0\\-4 \end{pmatrix} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: der\: Abstand\: d $
$\qquad$ $ d=|\overrightarrow{PF}| = \sqrt{0^2+0^2+(-4)^2}=4 $
$\:\:\:$ Der Abstand zwischen $P$ und $E$ ist:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large d=4\: LE $
Winkel und Abstände I
I- Winkel
- Winkel zwischen zwei Geraden $g_1$ und $g_2$
- Winkel zwischen eine Gerade $g$ und eine Ebene $E$
- Winkel zwischen zwei Ebenen $E_1$ und $E_2$
Schneiden sich zwei Geraden $g:\vec{x}=\vec{p}+r\cdot \vec{u}$ und $h:\vec{x}=\vec{q+s\cdot\vec{v}}$, dann gilt für ihren Schnittwinkel $\alpha$:
$\qquad\qquad\qquad\qquad$ $ cos\: \alpha = \large \frac{|\vec{u}\cdot\vec{v}|}{|\vec{u}|\cdot|\vec{v}|} $.
Dabei ist der Schnittwinkel immer der kleinere der beiden Scheitelwinkel, die entstehen, wenn zwei Geraden sich schneiden.
Skizze
Beispielaufgaben
Berechne Schnittpunkt und Schnittwinkel der beiden Geraden
$ g:\vec{x} = \begin{pmatrix} 0\\1\\3 \end{pmatrix} +r\cdot \begin{pmatrix} 1\\2\\-1 \end{pmatrix} $ $\:\:$ und $\:\:$ $ h:\vec{x} = \begin{pmatrix} 1\\3\\2 \end{pmatrix} +s\cdot \begin{pmatrix} 3\\2\\-5 \end{pmatrix} . $
Lösung
$
g:\vec{x}
=
\begin{pmatrix}
0\\1\\3
\end{pmatrix}
+r\cdot
\begin{pmatrix}
1\\2\\-1
\end{pmatrix}
$
$\:\:$
und
$\:\:$
$
h:\vec{x}
=
\begin{pmatrix}
1\\3\\2
\end{pmatrix}
+s\cdot
\begin{pmatrix}
3\\2\\-5
\end{pmatrix}
$
Die Richtungsvektoren sind nicht linear abhängig. Also, entweder schneiden sie sich oder sie sind windschief.
Vektorgleichung (Einsatz $g=h$):
$ \Longleftrightarrow $ $ \begin{pmatrix} 0\\1\\3 \end{pmatrix} +r\cdot \begin{pmatrix} 1\\2\\-1 \end{pmatrix} $ $=$ $ \begin{pmatrix} 1\\3\\2 \end{pmatrix} +s\cdot \begin{pmatrix} 3\\2\\-5 \end{pmatrix} $
Verwandle in Gleichungssystem:
$ \Longleftrightarrow $ $ \begin{cases} 0+1\cdot r &=\:\:1+3\cdot s \\ 1+2\cdot r &=\:\:3+2\cdot s \\ 3+(-1)\cdot r &=\:\:2+(-5)\cdot s \\ \end{cases} $ $ \Longrightarrow $ $ \begin{cases} r &=\:\:1+3\cdot s \qquad\:\:\: (I)\\ 1+2\cdot r &=\:\:3+2\cdot s \qquad\:\:\: (II)\\ 3-1\cdot r &=\:\:2-5\cdot s \qquad \:\:\: (III) \end{cases} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: (I)\: in\: (II)\: oder\: (III)\: ein $
$ \qquad $ $In\: (II)$ $\Longrightarrow$ $1+2(1+3s)=3+2s$
$ \qquad\qquad\:\:\:\:\: $ $\Longleftrightarrow$ $3+6s=3+2s$ $\qquad | -3/+2s$
$ \qquad\qquad\:\:\:\:\: $ $\longrightarrow$ $s=0$
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: s\: in\: (I)\: ein $
$ \qquad\qquad\:\:\:\:\: $ $\Longrightarrow$ $r=1+3(0)$
$ \qquad\qquad\:\:\:\:\: $ $\longrightarrow$ $r=1$
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: r=1\: und\: s=0\: in\: Geraden\: g\: oder\: h\: ein $
$ \qquad $ $In\: g:$
$ \qquad $ $ \Large s= $ $ \begin{pmatrix} 0\\1\\3 \\ \end{pmatrix} +(1)\cdot \begin{pmatrix} 1\\2\\-1 \\ \end{pmatrix} $ $ \Large = $ $ \begin{pmatrix} 0+1\\1+2\\3-1 \\ \end{pmatrix} $ $ \Large = $ $ \begin{pmatrix} 1\\3\\2 \\ \end{pmatrix} $
Schnittpunkt:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large s \begin{pmatrix} 1\\3\\2 \\ \end{pmatrix} $
Schnittwinkel:
Benutze die Richtungsvektoren beiden Geraden:
$ \qquad $ Berechne das Skalarprodukt der Richtungsvektoren:
$ \qquad\qquad \begin{pmatrix} 1\\2\\-1 \\ \end{pmatrix} \cdot \begin{pmatrix} 3\\2\\-5 \\ \end{pmatrix} $ $ \Large = $ $ 1\cdot 3+2\cdot 2-1\cdot (-5) $ $ \Large = $ $12$
$ \qquad $ Betrag von: $\begin{pmatrix} 1\\2\\-1 \\ \end{pmatrix}$ ist gleich $ \sqrt{1^2+2^2+(-1)^2} $ $ \Large = $ $2,449$
$ \qquad $ Betrag von: $\begin{pmatrix} 3\\2\\-5 \\ \end{pmatrix}$ ist gleich $ \sqrt{3^2+2^2+(-5)^2} $ $ \Large = $ $6,164$
$ \qquad $ Also der Winkel ist gleich:
$ \qquad\qquad $ $ \alpha = cos^{-1} (\frac{12}{2,449\: \cdot \:6,164}) $ $ \Large = $ $37,371^{\circ}$
Schnittwinkel:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \alpha=37,371^{\circ} $
Die Richtungsvektoren sind nicht linear abhängig. Also, entweder schneiden sie sich oder sie sind windschief.
Vektorgleichung (Einsatz $g=h$):
$ \Longleftrightarrow $ $ \begin{pmatrix} 0\\1\\3 \end{pmatrix} +r\cdot \begin{pmatrix} 1\\2\\-1 \end{pmatrix} $ $=$ $ \begin{pmatrix} 1\\3\\2 \end{pmatrix} +s\cdot \begin{pmatrix} 3\\2\\-5 \end{pmatrix} $
Verwandle in Gleichungssystem:
$ \Longleftrightarrow $ $ \begin{cases} 0+1\cdot r &=\:\:1+3\cdot s \\ 1+2\cdot r &=\:\:3+2\cdot s \\ 3+(-1)\cdot r &=\:\:2+(-5)\cdot s \\ \end{cases} $ $ \Longrightarrow $ $ \begin{cases} r &=\:\:1+3\cdot s \qquad\:\:\: (I)\\ 1+2\cdot r &=\:\:3+2\cdot s \qquad\:\:\: (II)\\ 3-1\cdot r &=\:\:2-5\cdot s \qquad \:\:\: (III) \end{cases} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: (I)\: in\: (II)\: oder\: (III)\: ein $
$ \qquad $ $In\: (II)$ $\Longrightarrow$ $1+2(1+3s)=3+2s$
$ \qquad\qquad\:\:\:\:\: $ $\Longleftrightarrow$ $3+6s=3+2s$ $\qquad | -3/+2s$
$ \qquad\qquad\:\:\:\:\: $ $\longrightarrow$ $s=0$
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: s\: in\: (I)\: ein $
$ \qquad\qquad\:\:\:\:\: $ $\Longrightarrow$ $r=1+3(0)$
$ \qquad\qquad\:\:\:\:\: $ $\longrightarrow$ $r=1$
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: r=1\: und\: s=0\: in\: Geraden\: g\: oder\: h\: ein $
$ \qquad $ $In\: g:$
$ \qquad $ $ \Large s= $ $ \begin{pmatrix} 0\\1\\3 \\ \end{pmatrix} +(1)\cdot \begin{pmatrix} 1\\2\\-1 \\ \end{pmatrix} $ $ \Large = $ $ \begin{pmatrix} 0+1\\1+2\\3-1 \\ \end{pmatrix} $ $ \Large = $ $ \begin{pmatrix} 1\\3\\2 \\ \end{pmatrix} $
Schnittpunkt:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large s \begin{pmatrix} 1\\3\\2 \\ \end{pmatrix} $
Schnittwinkel:
Benutze die Richtungsvektoren beiden Geraden:
$ \qquad $ Berechne das Skalarprodukt der Richtungsvektoren:
$ \qquad\qquad \begin{pmatrix} 1\\2\\-1 \\ \end{pmatrix} \cdot \begin{pmatrix} 3\\2\\-5 \\ \end{pmatrix} $ $ \Large = $ $ 1\cdot 3+2\cdot 2-1\cdot (-5) $ $ \Large = $ $12$
$ \qquad $ Betrag von: $\begin{pmatrix} 1\\2\\-1 \\ \end{pmatrix}$ ist gleich $ \sqrt{1^2+2^2+(-1)^2} $ $ \Large = $ $2,449$
$ \qquad $ Betrag von: $\begin{pmatrix} 3\\2\\-5 \\ \end{pmatrix}$ ist gleich $ \sqrt{3^2+2^2+(-5)^2} $ $ \Large = $ $6,164$
$ \qquad $ Also der Winkel ist gleich:
$ \qquad\qquad $ $ \alpha = cos^{-1} (\frac{12}{2,449\: \cdot \:6,164}) $ $ \Large = $ $37,371^{\circ}$
Schnittwinkel:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \alpha=37,371^{\circ} $
$\:\:$Schneiden sich eine Gerade $g:\vec{x}=\vec{p}+t\cdot \vec{u}$ und eine Ebene $E:\vec{n}\cdot[\vec{x}-\vec{a}]$, dann gilt für
$\:\:$ihren Schnittwinkel $\alpha$ zwischen dem Richtungsvektor der Gerade und dem Normalenvektor $\:\:$der Ebene:
$\qquad\qquad\qquad\qquad$ $ cos\: \alpha = \large \frac{|\vec{r}\cdot\vec{n}|}{|\vec{r}|\cdot|\vec{n}|} $.
$\:\:$Ist $\vec{s}$ ein Richtungsvektor der Schnittgeraden zwischen der Ebene E und der zu E
$\:\:$senkrechten Ebene F, in der $g$ liegt, dann gilt für den Winkel $\beta$ zwischen $\vec{r}$ und $\vec{s}:$ $\:\:\beta=90{^\circ}-\alpha.$ Es gilt also
$\qquad\qquad\qquad\qquad$ $ sin\: \beta = \large \frac{|\vec{r}\cdot\vec{n}|}{|\vec{r}|\cdot|\vec{n}|} $.
Beispielaufgabe
Berechne den Schnittwinkel zwischen der Gerade $g$ und der Ebene $E.$
$ g:\vec{x} = \begin{pmatrix} 3\\6\\-5 \end{pmatrix} +t\cdot \begin{pmatrix} -1\\4\\3 \end{pmatrix} $ $\:\:$ und $\:\:$ $ E: \begin{bmatrix}\vec{x}- \begin{pmatrix} 2\\9\\3 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 2\\-2\\3 \end{pmatrix} $
Lösung
$
g:\vec{x}
=
\begin{pmatrix}
3\\6\\-5
\end{pmatrix}
+t\cdot
\begin{pmatrix}
-1\\4\\3
\end{pmatrix}
$
$\:\:$
und
$\:\:$
$
E:
\begin{bmatrix}\vec{x}-
\begin{pmatrix}
2\\9\\3
\end{pmatrix}
\end{bmatrix}
\cdot
\begin{pmatrix}
2\\-2\\3
\end{pmatrix}
$
Bestimme die Koordinatenform von $E$:
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Multipliziere\: E\: aus $
$ \:\:\: $ $ E: \begin{bmatrix}\vec{x}- \begin{pmatrix} 2\\9\\3 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 2\\-2\\3 \end{pmatrix} $ $=$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 2\\-2\\3 \end{pmatrix}- \begin{pmatrix} 2\\9\\3 \end{pmatrix} \cdot \begin{pmatrix} 2\\-2\\3 \end{pmatrix} =0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Skalarprodukt\: berechnen $
$ \:\:\: $ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 2\\-2\\3 \end{pmatrix} $ $=$ $ 2x-2y+3z $ $\qquad | \qquad $ $ \begin{pmatrix} 2\\9\\3 \end{pmatrix} \cdot \begin{pmatrix} 2\\-2\\3 \end{pmatrix} = 2\cdot2+9\cdot (-2)+3\cdot 3=-5 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Setze\: beiden\:Ergebnisse\: in\: die\: ausmultiplizierte\: Normalenform\: ein $
$ \:\:\:\:\:\: $ $ \longrightarrow $ die Koordinatenform: $E:2x-2y+3z=-5$
$ \qquad\:\:\:\:\:\: $ und den Normalenvektor: $\vec{n}=\begin{pmatrix}2\\-2\\3\end{pmatrix}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: Skalarprodukt\: von\: Normalenvektor\: (E)\: und\: Richtungsvektor\: (g) $
$ \:\:\: $ $ \begin{pmatrix} -1\\4\\3 \end{pmatrix} \cdot \begin{pmatrix} 2\\-2\\3 \end{pmatrix} = -1\cdot 2+4\cdot (-2)+3\cdot 3=-1 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Betrag\: von\:(E)\: und\: (g) $
$ \:\:\: $ Betrag von $ \begin{pmatrix} -1\\4\\3 \end{pmatrix} $ ist $ \sqrt{(-1)^2+4^2+3^2}=5,09 $
$ \:\:\: $ Betrag von $ \begin{pmatrix} 2\\-2\\3 \end{pmatrix} $ ist $ \sqrt{2^2+(-2)^2+3^2}=4,12 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: der\: Winkel $
$ \:\:\:\:\: $ $ \alpha=sin^{-1} \frac{|-1|}{5,09\: \cdot \:4,12}=2,73^{\circ} $
Der Schnittwinkel zwischen der Gerade $g$ und der Ebene $E$ lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \alpha=2,73^{\circ} $
Bestimme die Koordinatenform von $E$:
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Multipliziere\: E\: aus $
$ \:\:\: $ $ E: \begin{bmatrix}\vec{x}- \begin{pmatrix} 2\\9\\3 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 2\\-2\\3 \end{pmatrix} $ $=$ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 2\\-2\\3 \end{pmatrix}- \begin{pmatrix} 2\\9\\3 \end{pmatrix} \cdot \begin{pmatrix} 2\\-2\\3 \end{pmatrix} =0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Skalarprodukt\: berechnen $
$ \:\:\: $ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 2\\-2\\3 \end{pmatrix} $ $=$ $ 2x-2y+3z $ $\qquad | \qquad $ $ \begin{pmatrix} 2\\9\\3 \end{pmatrix} \cdot \begin{pmatrix} 2\\-2\\3 \end{pmatrix} = 2\cdot2+9\cdot (-2)+3\cdot 3=-5 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Setze\: beiden\:Ergebnisse\: in\: die\: ausmultiplizierte\: Normalenform\: ein $
$ \:\:\:\:\:\: $ $ \longrightarrow $ die Koordinatenform: $E:2x-2y+3z=-5$
$ \qquad\:\:\:\:\:\: $ und den Normalenvektor: $\vec{n}=\begin{pmatrix}2\\-2\\3\end{pmatrix}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: Skalarprodukt\: von\: Normalenvektor\: (E)\: und\: Richtungsvektor\: (g) $
$ \:\:\: $ $ \begin{pmatrix} -1\\4\\3 \end{pmatrix} \cdot \begin{pmatrix} 2\\-2\\3 \end{pmatrix} = -1\cdot 2+4\cdot (-2)+3\cdot 3=-1 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Betrag\: von\:(E)\: und\: (g) $
$ \:\:\: $ Betrag von $ \begin{pmatrix} -1\\4\\3 \end{pmatrix} $ ist $ \sqrt{(-1)^2+4^2+3^2}=5,09 $
$ \:\:\: $ Betrag von $ \begin{pmatrix} 2\\-2\\3 \end{pmatrix} $ ist $ \sqrt{2^2+(-2)^2+3^2}=4,12 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: der\: Winkel $
$ \:\:\:\:\: $ $ \alpha=sin^{-1} \frac{|-1|}{5,09\: \cdot \:4,12}=2,73^{\circ} $
Der Schnittwinkel zwischen der Gerade $g$ und der Ebene $E$ lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \alpha=2,73^{\circ} $
$\:\:\:$Schneiden sich zwei Ebenen $E_1$ und $E_2$, mit den Normalenvektor $\vec{n_1}$ und $\vec{n_2}$,
$\:\:$dan gilt für den Schnittwinkel $\alpha$:
$\qquad\qquad\qquad\qquad$ $ cos\: \alpha = \large \frac{|\vec{n_1}\cdot\vec{n_2}|}{|\vec{n_1}|\cdot|\vec{n_2}|} $.
Beispielaufgabe
Berechne den Schnittwinkel zwischen $E_1$ und $E_2$.
$\qquad$ $E_1: 3x+2y-z=1 \:\:\:\:$ und $\:\:\:\: E_2: -2x+2y+5=-1$
Lösung
$\qquad$ $E_1: 3x+2y-z=1 \:\:\:\:$ und $\:\:\:\: E_2: -2x+2y+5=-1$
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Schreibe\: Normalenvektoren\: von\: E_1\: und\: E_2 $
$ \qquad $ $ \vec{n_1}= \begin{pmatrix} 3\\2\\-1 \end{pmatrix} $ $\:\:\:\:$ und $\:\:\:\:$ $ \vec{n_2}= \begin{pmatrix} -2\\2\\5 \end{pmatrix} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Berechne\: das\: Skalarprodukt\: der\: \:beiden\: Normalenvektoren $
$ \qquad $ $ \begin{pmatrix} 3\\2\\-1 \end{pmatrix} \cdot \begin{pmatrix} -2\\2\\5 \end{pmatrix} =3\cdot (-2)+2\cdot 2+ (-1)\cdot 5=-7 $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Betrag\: von\: \vec{n_1} \: und\: \vec{n_2} $
$ \qquad $ Betrag von $\vec{n_1}$ ist gleich: $|\vec{n_1}|=\sqrt{3^2+2^2+(-1)^2}=3,741$
$ \qquad $ Betrag von $\vec{n_2}$ ist gleich: $|\vec{n_2}|=\sqrt{(-2)^2+2^2+5^2}=5,744$
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Berechne\: der\: Winkel\: \alpha $
$ \qquad $ $ \alpha=cos^{-1}\frac{|-7|}{3.741\: \cdot \: 5,744}=70,988^{\circ} $
$ \qquad $ Schnittwinkel:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \alpha\approx 70,99^{\circ} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Schreibe\: Normalenvektoren\: von\: E_1\: und\: E_2 $
$ \qquad $ $ \vec{n_1}= \begin{pmatrix} 3\\2\\-1 \end{pmatrix} $ $\:\:\:\:$ und $\:\:\:\:$ $ \vec{n_2}= \begin{pmatrix} -2\\2\\5 \end{pmatrix} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Berechne\: das\: Skalarprodukt\: der\: \:beiden\: Normalenvektoren $
$ \qquad $ $ \begin{pmatrix} 3\\2\\-1 \end{pmatrix} \cdot \begin{pmatrix} -2\\2\\5 \end{pmatrix} =3\cdot (-2)+2\cdot 2+ (-1)\cdot 5=-7 $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Berechne\: den\: Betrag\: von\: \vec{n_1} \: und\: \vec{n_2} $
$ \qquad $ Betrag von $\vec{n_1}$ ist gleich: $|\vec{n_1}|=\sqrt{3^2+2^2+(-1)^2}=3,741$
$ \qquad $ Betrag von $\vec{n_2}$ ist gleich: $|\vec{n_2}|=\sqrt{(-2)^2+2^2+5^2}=5,744$
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Berechne\: der\: Winkel\: \alpha $
$ \qquad $ $ \alpha=cos^{-1}\frac{|-7|}{3.741\: \cdot \: 5,744}=70,988^{\circ} $
$ \qquad $ Schnittwinkel:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \alpha\approx 70,99^{\circ} $
Übungsaufgaben – Winkel
Berechne Schnittpunkt und Schnittwinkel der beiden Geraden
-
$g: \vec{x}=
\begin{pmatrix}
4\\3\\1
\end{pmatrix}+
r\cdot
\begin{pmatrix}
-1\\-1\\1
\end{pmatrix}
$
$\:\:\:$
und
$\:\:\:$
$h: \vec{x}=
\begin{pmatrix}
-3\\-4\\-1
\end{pmatrix}+
s\cdot
\begin{pmatrix}
2\\2\\1
\end{pmatrix}
$
Lösung$ g:\vec{x} = \begin{pmatrix} 4\\3\\1 \end{pmatrix} +r\cdot \begin{pmatrix} -1\\-1\\1 \end{pmatrix} $ $\:\:$ und $\:\:$ $ h:\vec{x} = \begin{pmatrix} -3\\-4\\-1 \end{pmatrix} +s\cdot \begin{pmatrix} 2\\2\\1 \end{pmatrix} $
Die Richtungsvektoren sind nicht linear abhängig. Also, entweder schneiden sie sich oder sie sind windschief.
Vektorgleichung (Einsatz $g=h$):
$ \Longleftrightarrow $ $ \begin{pmatrix} 4\\3\\1 \end{pmatrix} +r\cdot \begin{pmatrix} -1\\-1\\1 \end{pmatrix} $ $=$ $ \begin{pmatrix} -3\\-4\\-1 \end{pmatrix} +s\cdot \begin{pmatrix} 2\\2\\1 \end{pmatrix} $
Verwandle in Gleichungssystem:
$ \Longleftrightarrow $ $ \begin{cases} 4+(-1)\cdot r &=\:\:(-3)+2\cdot s \\ 3+(-1)\cdot r &=\:\:(-4)+2\cdot s \\ 1+1\cdot r &=\:\:(-1)+1\cdot s \\ \end{cases} $ $ \Longrightarrow $ $ \begin{cases} 4-r &=\:\:-3+2\cdot s \qquad\:\:\: (I)\\ 3-r &=\:\:-4+2\cdot s \qquad\:\:\: (II)\\ 1+r &=\:\:-1+1\cdot s \qquad \:\:\: (III) \end{cases} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Addiere\: (II)\: und\: (III) $
$ \qquad $ $\Longrightarrow$ $4=-5+3s$ $\qquad | +5/(:3)$
$ \qquad\qquad $ $\longrightarrow$ $s=3$
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: s\: in\: (I)\: ein $
$ \qquad $ $\Longrightarrow$ $4-r=-3+2\cdot3$
$ \qquad $ $\Longrightarrow$ $4-r=3$ $\qquad | -4/:(-1)$
$ \qquad\qquad $ $\longrightarrow$ $r=1$
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: r=1\: und\: s=3\: in\: Geraden\: g\: oder\: h\: ein $
$ \qquad $ $In\: h:$
$ \qquad $ $ \Large s= $ $ \begin{pmatrix} -3\\-4\\-1 \\ \end{pmatrix} +(3)\cdot \begin{pmatrix} 2\\2\\1 \\ \end{pmatrix} $ $ \Large = $ $ \begin{pmatrix} -3+6\\-4+6\\-1+3 \\ \end{pmatrix} $ $ \Large = $ $ \begin{pmatrix} 3\\2\\2 \\ \end{pmatrix} $
Schnittpunkt:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large s \begin{pmatrix} 3\\2\\2 \\ \end{pmatrix} $
Schnittwinkel:
Benutze die Richtungsvektoren beiden Geraden:
$ \qquad $ Berechne das Skalarprodukt der Richtungsvektoren:
$ \qquad\qquad \begin{pmatrix} -1\\-1\\1 \\ \end{pmatrix} \cdot \begin{pmatrix} 2\\2\\1 \\ \end{pmatrix} $ $ \Large = $ $ -1\cdot 2+(-1)\cdot 2+1\cdot 1 $ $ \Large = $ $-3$
$ \qquad $ Betrag von: $\begin{pmatrix} -1\\-1\\1 \\ \end{pmatrix}$ ist gleich $ \sqrt{(-1)^2+(-1)^2+1^2} $ $ \Large = $ $1,732$
$ \qquad $ Betrag von: $\begin{pmatrix} 2\\2\\1 \\ \end{pmatrix}$ ist gleich $ \sqrt{2^2+2^2+1^2} $ $ \Large = $ $3$
$ \qquad $ Also der Winkel ist gleich:
$ \qquad\qquad $ $ \alpha = cos^{-1} (\frac{-3}{1,732\: \cdot \:3}) $ $ \Large = $ $125,264^{\circ}$
Schnittwinkel:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \alpha=125,264^{\circ} $ -
$g: \vec{x}=
\begin{pmatrix}
3\\2\\0
\end{pmatrix}+
r\cdot
\begin{pmatrix}
-1\\2\\4
\end{pmatrix}
$
$\:\:\:$
und
$\:\:\:$
$h: \vec{x}=
\begin{pmatrix}
2\\1\\0
\end{pmatrix}+
s\cdot
\begin{pmatrix}
-2\\1\\4
\end{pmatrix}
$
$\:\:$$s\begin{pmatrix}4\\0\\-4\end{pmatrix};$ $\alpha=17,753^{\circ}$ -
$g: \vec{x}=
\begin{pmatrix}
-1\\-2\\6
\end{pmatrix}+
r\cdot
\begin{pmatrix}
2\\2\\-1
\end{pmatrix}
$
$\:\:\:$
und
$\:\:\:$
$h: \vec{x}=
\begin{pmatrix}
1\\3\\11
\end{pmatrix}+
s\cdot
\begin{pmatrix}
0\\1\\2
\end{pmatrix}
$
$\:\:$$s\begin{pmatrix}1\\0\\5\end{pmatrix};$ $\alpha=90^{\circ}$
Berechne den Schnittwinkel zwischen der Gerade $g$ und der Ebene $E$.
-
$
g:\vec{x}
=
\begin{pmatrix}
2\\2\\1
\end{pmatrix}
+r\cdot
\begin{pmatrix}
1\\-1\\1
\end{pmatrix}
$
$\:\:$
und
$\:\:$
$
E:\vec{x}
=
\begin{pmatrix}
1\\1\\5
\end{pmatrix}
+s\cdot
\begin{pmatrix}
2\\0\\1
\end{pmatrix}
+t\cdot
\begin{pmatrix}
-1\\-1\\3
\end{pmatrix}
$
Lösung$ g:\vec{x} = \begin{pmatrix} 2\\2\\1 \end{pmatrix} +r\cdot \begin{pmatrix} 1\\-1\\1 \end{pmatrix} $ $\:\:$ und $\:\:$ $ E:\vec{x} = \begin{pmatrix} 1\\1\\5 \end{pmatrix} +s\cdot \begin{pmatrix} 2\\0\\1 \end{pmatrix} +t\cdot \begin{pmatrix} -1\\-1\\3 \end{pmatrix} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Gleiche\: die\: Vektoren:\: Einsatz\: (g=E) $
$ \begin{pmatrix} 2\\2\\1 \end{pmatrix} +r\cdot \begin{pmatrix} 1\\-1\\1 \end{pmatrix} $ $=$ $ \begin{pmatrix} 1\\1\\5 \end{pmatrix} +s\cdot \begin{pmatrix} 2\\0\\1 \end{pmatrix} +t\cdot \begin{pmatrix} -1\\-1\\3 \end{pmatrix} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Schreibe\: als\: Lineares\: Gleichungssystem\: (LGS) $
$ \qquad $ $ \begin{cases} 2+r &=1+2s-t\\ 2-r &=1+0s-t\\ 1+r &=5+s+3t \end{cases} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Bringe\: Zahlen\: nach\: rechts\: und\: Variablen\: nach\: links $
$ \qquad $ $ \begin{cases} r-2s+t &=-1 \qquad (I)\\ -r+t &=-1 \qquad (II)\\ r-s-3t &=4 \qquad\:\:\: (III) \end{cases} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Schreibe\: (II)\: nach\: r $
$ \qquad $ $ \begin{cases} r-2s+t &=-1\\ r &=1+t\\ r-s-3t &=4 \end{cases} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Setzte\: r\: in\: (I)\: und\: (III) $
$ \qquad $ $ \begin{cases} 1+t-2s+t &=-1\\ 1+t-s-3t &=4 \end{cases} $ $\:\:$ $\Longrightarrow$ $\:\:$ $ \begin{cases} 2t-2s &=-2\\ -2t-s &=3 \end{cases} $
$ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Addiere\: (I)\: und\: (III) $
$ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad $ $ -3s=1 \qquad | :(-3) $
$ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad $ $\longrightarrow$ $ s=-\frac{1}{3} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Setzte\: s\: in\: (I)\: und\: (III) $
$ \qquad $ $ \begin{cases} r-2\cdot (-\frac{1}{3})+t &=-1\\ r-1\cdot (-\frac{1}{3})-3t &=4 \end{cases} $ $\:\:$ $\underrightarrow{Fasse\: zusammen}$ $\:\:$ $ \begin{cases} r+t &=-\frac{5}{3}\\ r-3t &=\frac{11}{3} \end{cases} $
$ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Subtrahiere $
$ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad $ $ 4t=-\frac{16}{3} \qquad | :(-\frac{16}{3}) $
$ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad $ $ \longrightarrow $ $ t=-\frac{4}{3} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Setzte\: t\: in\: r=1+t\: ein $
$ \qquad\:\: $ $ r=1-\frac{4}{3} $ $ \longrightarrow $ $ r=-\frac{1}{3} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Setzte\: die\: Werte\: in\: Ebene\: ein $
$ \qquad $ $ \begin{pmatrix} 1\\1\\5 \end{pmatrix} +(-\frac{1}{3})\cdot \begin{pmatrix} 2\\0\\1 \end{pmatrix} +(-\frac{4}{3})\cdot \begin{pmatrix} -1\\-1\\3 \end{pmatrix} $ $=$ $ \begin{pmatrix} 1-\frac{2}{3}+\frac{4}{3}\\ 1+0+\frac{4}{3}\\ 5-\frac{1}{3}-4 \end{pmatrix} $ $=$ $ \begin{pmatrix} \frac{5}{3}\\ \frac{7}{3}\\ \frac{2}{3} \end{pmatrix} $
$ \qquad $ Schnittpunkt:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \Large s \begin{pmatrix} \frac{5}{3}\\ \frac{7}{3}\\ \frac{2}{3} \end{pmatrix} $
$ \qquad $ Schnittwinkel:
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Schreibe\: E\: in\: Koordinatenform $
$ \qquad\qquad $ – Bestimme die Normalenform von $E:$
$ \qquad\qquad\qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Bestimme\: das\: Kreuzprodukt\: der\: Richtungsvektoren $
$ \qquad\qquad\qquad $ $ \begin{pmatrix} 2\\0\\1 \end{pmatrix} \times \begin{pmatrix} -1\\-1\\3 \end{pmatrix} $ $=$ $ \begin{pmatrix} 0\cdot 3-1\cdot (-1)\\ 1\cdot (-1)-2\cdot 3\\ 2\cdot (-1)-0\cdot (-1) \end{pmatrix} $ $=$ $ \begin{pmatrix} 1\\-7\\-2 \end{pmatrix} $
$ \qquad\qquad\qquad $ $\longrightarrow$ Normalengleichung: $ E:\begin{bmatrix} x- \begin{pmatrix} 1\\1\\5 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 1\\-7\\-2 \end{pmatrix} =0 $
$ \qquad\qquad $ – Bestimme die Koordinatenform von $E:$
$ \qquad\qquad\qquad $ $ E:\begin{bmatrix} x- \begin{pmatrix} 1\\1\\5 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 1\\-7\\-2 \end{pmatrix} =0 $
$ \qquad\qquad\qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Multipliziere\: aus $
$ \qquad\qquad\qquad $ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 1\\-7\\-2 \end{pmatrix} = x-7y-2z $
$ \qquad\qquad\qquad $ $ \begin{pmatrix} 1\\1\\5 \end{pmatrix} \cdot \begin{pmatrix} 1\\-7\\-2 \end{pmatrix} = 1\cdot1+1\cdot (-7)+5\cdot (-2)=-16 $
$ \qquad\qquad\qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Setzte\: die\: beiden\: Ergebnisse\: in\: die\: Normaleform\: ein $
$ \qquad\qquad\qquad $ $\longrightarrow$ Koordinatenform: $E:x-7y-2z=-16$
$ \qquad\qquad\qquad $ $\longrightarrow$ Normalenvektor: $ \vec{n}= \begin{pmatrix} 1\\-7\\-2 \end{pmatrix} $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Berechne\: das\: Skalarprodukt\: von\: Normalenvektor(E)\: und\: Richtungsvektor(g) $
$ \qquad $ $ \begin{pmatrix} 1\\-1\\1 \end{pmatrix} \cdot \begin{pmatrix} 1\\-7\\-2 \end{pmatrix} = 1\cdot 1+(-1)\cdot (-7)+1\cdot (-2)=6 $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Berechne\: Betrag\: von\: (E)\: und\: (g) $
$ \qquad\qquad $ Betrag von $ \begin{pmatrix} 1\\-1\\1 \end{pmatrix} $ ist $ \sqrt{1^2+(-1)^2+1^2}=1,732 $
$ \qquad\qquad $ Betrag von $ \begin{pmatrix} 1\\-7\\-2 \end{pmatrix} $ ist $ \sqrt{1^2+(-7)^2+(-2)^2}=7,348 $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Berechne\: der\: Winkel $
$ \qquad $ $\longrightarrow$ $ \large \alpha=sin^{-1}=\frac{6}{1,732\: \cdot \: 7,348}=28,128^{\circ} $
$ \qquad $ Schnittwinkel:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \alpha\approx28,13^{\circ} $ -
$
g:\vec{x}
=
\begin{pmatrix}
2\\-3\\4
\end{pmatrix}
+r\cdot
\begin{pmatrix}
6\\2\\4
\end{pmatrix}
$
$\:\:$
und
$\:\:$
$
E:
\begin{bmatrix}
\vec{x}
–
\begin{pmatrix}
1\\0\\-5
\end{pmatrix}
\end{bmatrix}
+s\cdot
\begin{pmatrix}
3\\5\\-1
\end{pmatrix}
$
$\:\:$$\alpha\approx32,83^{\circ}$ -
$
g:\vec{x}
=
\begin{pmatrix}
2\\8\\8
\end{pmatrix}
+r\cdot
\begin{pmatrix}
3\\4\\3
\end{pmatrix}
$
$\:\:$
und
$\:\:$
$
E:2x-4y+3z=5
$
$\:\:$$\alpha\approx1,83^{\circ}$
Berechne den Schnittwinkel zwischen den Ebenen $E_1$ und $E_2$.
-
$
E_1:
\begin{bmatrix}
\vec{x}
–
\begin{pmatrix}
4\\-3\\5
\end{pmatrix}
\end{bmatrix}
\cdot
\begin{pmatrix}
2\\-4\\1
\end{pmatrix}
=0
$
$\:\:$
und
$\:\:$
$
E_2:-6x+4y-3z=4
$
Lösung$ E_1: \begin{bmatrix} \vec{x} – \begin{pmatrix} 4\\-3\\5 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 2\\-4\\1 \end{pmatrix} =0 $ $\:\:$ und $\:\:$ $ E_2:-6x+4y-3z=4 $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Für\: Normalenvektor\: von\: E_1\: Schreibe\: in\: der\: Koordinatenform $
$ \qquad $ $ E_1: \begin{bmatrix} \begin{pmatrix} x\\y\\z \end{pmatrix} – \begin{pmatrix} 4\\-3\\5 \end{pmatrix} \end{bmatrix} \cdot \begin{pmatrix} 2\\-4\\1 \end{pmatrix} =0 $
$ \qquad $ $ \Large \Bigg\downarrow $ $ \normalsize Multipliziere\: aus $
$ \qquad $ $ \begin{pmatrix} x\\y\\z \end{pmatrix} \cdot \begin{pmatrix} 2\\-4\\1 \end{pmatrix} = 2x-4y+z $
$ \qquad $ $ \begin{pmatrix} 4\\-3\\5 \end{pmatrix} \cdot \begin{pmatrix} 2\\-4\\1 \end{pmatrix} = 4\cdot2+ (-3)\cdot(-4)+5\cdot 1=25 $
$ \qquad $ Die Koordinatenform lautet: $E_1: 2x-4y+z=25$
$ \qquad $ Den Normalenvektor von $E_1$ lautet: $n_1 = \begin{pmatrix} 2\\-4\\1 \end{pmatrix} $
$ \qquad $ Den Normalenvektor von $E_2$ lautet: $n_2 = \begin{pmatrix} -6\\4\\-3 \end{pmatrix} $
$ \qquad $ Schnittwinkel
$ \qquad\qquad\qquad $ $ \alpha=cos^{-1} \frac { \large \begin{vmatrix} \begin{pmatrix} 2\\-4\\1 \end{pmatrix} \cdot \begin{pmatrix} -6\\4\\-3 \end{pmatrix} \end{vmatrix} } { \large \begin{vmatrix} \begin{pmatrix} 2\\-4\\1 \end{pmatrix} \end{vmatrix} \cdot \begin{vmatrix} \begin{pmatrix} -6\\4\\-3 \end{pmatrix} \end{vmatrix} }= 29,987^{\circ} $
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \alpha\approx29,99^{\circ} $ -
$
E_1:6x-2y-3z=7
$
$\:\:$
und
$\:\:$
$
E_2:\vec{x}
=
\begin{pmatrix}
2\\0\\-4
\end{pmatrix}
+
\lambda
\cdot
\begin{pmatrix}
3\\-4\\2
\end{pmatrix}
+
\mu
\cdot
\begin{pmatrix}
4\\-1\\5
\end{pmatrix}
$
$\:\:$$n_2$ $=$ $ \begin{pmatrix} 18\\-7\\13 \end{pmatrix}, $ $\:$ $\alpha\approx35,3^{\circ}$ -
$
E_1:2x+y+2z=-8
$
$\:\:$
und
$\:\:$
$
E_2:6x+3y+2z=-12
$
$\:\:$$\alpha\approx25,20^{\circ}$
Lineares Gleichungssystem
Lineares Gleichungssystem
Ein lineares Gleichungssystem (kurz LGS) besteht aus mehreren linearen Gleichungen mit gemeinsamen Unbekannten (Variablen) zusammen.
Jede Variable wird mit höchstens dem Exponenten 1 geschrieben.
Ein lineares Gleichungssystem lässt sich lösen, mit mindestens so viele Gleichungen, wie es Unbekannte gibt.
Lineares Gleichungssystem lösen
Um ein lineares Gleichungssystem zu lösen musst du alle Variablen so bestimmen, dass alle Gleichungen des Systems erfüllt werden.
Es gibt fünf verschiedene Verfahren, ein Gleichungssystem zu lösen:
- Das Additionsverfahren: durch Addition bzw. Subtraktion der Gleichungen wird eine der unbekannten $x$ oder $y$ isoliert (aufgehoben), um die Bestimmung der anderen zu ermöglichen.
- Das Einsetzungsverfahren: eine Gleichung wird nach einer Variablen $x$ oder $y$ umgeformt und in die andere Gleichung eingesetzt.
- Das Gleichsetzungsverfahren: die beiden linearen Gleichungen des linearen Gleichungssystems werden nach derselben Variablen $x$ oder $y$ aufgelöst und die entsprechenden Terme gleichgesetzt.
- Das Gaußverfahren oder gaußsche Eliminationsverfahren: wird benutzt um Gleichungen mit viele unterschiedliche Variablen zu lösen.
- Cramersche Regel oder Determinantenmethode: wird für kleines Gleichungssystem benutzt, die eindeutig lösbar sind.
Übungsaufgaben
- Löse mit dem Additionsverfahren:
$ \begin{cases} \begin{align*} \:\: 15x\:\: -2y\:\: &=\:\: 44 \\ \:\: 10x\:\: -3y\:\: &=\:\: 16 \end{align*} \end{cases} $
Lösung$ \begin{cases} \begin{align*} \:\: 15x\:\: -2y\:\: &=\:\: 44 \:\:(I) \\ \:\: 10x\:\: -3y\:\: &=\:\: 16 \:\:(II) \end{align*} \end{cases} $
$ 3\cdot (I) + (-2)\cdot (II) \:\: \Rightarrow \:\: \begin{cases} &45x-6y=132 \\ -&20x+6y=-32 \\ \hline \end{cases} $
$\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ 25x+0y=100 \:\:| :25 \\ $
$\qquad\qquad\qquad\qquad\qquad\qquad$ $ \large \longrightarrow x=4 $
Setze $x=4$ in $(I)$ ein
$\qquad\qquad\qquad\qquad\:\:$ $ \Rightarrow \:\: 15(4)-2y=44 \:\:\:\:\:\:\: |\:(-60) $
$\qquad\qquad\qquad\qquad\:\:$ $ \Rightarrow \qquad\:\:\:\:\: -2y=-16 \:\:\:\: |\:(-2) $
$\qquad\qquad\qquad\qquad\qquad\qquad$ $ \large \longrightarrow y=8 $
Die Lösungsmenge lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \mathbb{L}=\{(4|8)\} $
Graphische Darstellung$\qquad$ $ \large \textcolor{DodgerBlue}{ y_1=7,5x-22 } $ $\qquad$ $ \large \textcolor{OliveGreen}{ y_2=3,3x-5,33 } $
$ \begin{cases} \begin{align*} -4x\:\: +\:\: &3y \:\:=\:\: 6\\ 3x\:\: -\:\: &6y \:\:=\:\: 3 \end{align*} \end{cases} $
Lösung$ \small \begin{cases} \begin{align*} -4x\:\: +\:\: &3y \:\:=\:\: 6 \:\: (I)\\ 3x\:\: -\:\: &6y \:\:=\:\: 3 \:\: (II) \end{align*} \end{cases} $
$ \:\:\: \small 2\cdot (I) + (II) $ $ \Large \Bigg\downarrow $ $ \normalsize Multipliziere\: (I)\: Mal\: 2\: und\: addiere\: mit\: (II). $
$ \small \begin{cases} \begin{align*} -8x\:\: +\:\: &6y \:\:=\:\: 12 \:\: \\ 3x\:\: -\:\: &6y \:\:=\:\: 3 \:\:\\ \hline -5x\:\: +\:\: &\textcolor{red}{0y} \:\:=\:\: 15 \:\:(III) \end{align*} \end{cases} $
$ \:\:\:\: \small (III):(-5) $ $ \: \Large \Bigg\downarrow $ $ \normalsize Teile\: (III)\: durch\: (-5). $
$\qquad\qquad\qquad$ $ \LARGE \longrightarrow $ $ \large x=-3 $ $ \:\: \small (IV) $
$ \:\:\:\: \small (IV) \:in\: (II) $ $ \: \Large \Bigg\downarrow $ $ \normalsize Setze\: (IV)\: in\: (II)\: ein. $
$ \qquad\qquad \small 3\cdot (-3)-6y=3 $
$ \qquad\qquad\qquad \Large \Bigg\downarrow $ $ \normalsize Fasse\: zusammen\: und\: löse\: nach\: y\: auf. $
$ \qquad\qquad \small -9-6y=3 \qquad | +9 \:\:\:\:\:\:\:\:\: (Rechne\:Plus\: 9). $
$ \qquad\qquad \small -6y=12 \qquad\:\:\:\:\:\:| :(-6) \:\:\:\:(Divide\: durch\: (-6)). $
$\qquad\qquad\qquad$ $ \LARGE \longrightarrow $ $ \large y=-2 $
Die Lösungsmenge lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \mathbb{L}=\{(-3|-2)\} $
Graphische Darstellung$\qquad$ $ \large \textcolor{DodgerBlue}{ y_1=\frac{4}{3}x+2 } $ $\qquad$ $ \large \textcolor{OliveGreen}{ y_2=\frac{1}{2}x-\frac{1}{2} } $
- Löse mit dem Einsetzungsverfahren:
$ \begin{cases} \begin{align*} \:\: 3x\:\: -\: 4y\:\: &=\:\: -6 \\ \:\: 2x\:\: +\: 3y\:\: &=\:\: 13 \end{align*} \end{cases} $
Lösung$ \begin{cases} \begin{align*} \:\: 3x\:\: -\: 4y\:\: &=\:\: -6 \:\: (I)\\ \:\: 2x\:\: +\: 3y\:\: &=\:\: 13 \:\: (II) \end{align*} \end{cases} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Stelle\: (II)\: nach\: x\: um: $
$ 2x+3y=13 \qquad |-3y \:\:\:(Rechne\: Minus\: 3y) $
$ 2x=13-3y \qquad |:2 \:\:\:(Dividiere\: durch\: 2) $
$ \:\:\:\: $ $ \LARGE \longrightarrow $ $ \large x=6,5-1,5y $ $ \normalsize \:\:\: (III) $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: (III)\: in\: (I)\: ein: $
$ 3\cdot (6,5-1,5y)-4y=-6 $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Klammere\: auf\: und\: fasse\: zusammen\: nach\: y: $
$ 3\cdot (6,5-1,5y)-4y=-6 \qquad\qquad\qquad |\:Klammer\: auflösen $
$ 19,5-4,5y-4y=-6 \qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: |\:Zusammenfassen $
$ 19,5-8,5y=-6 \qquad\qquad\qquad\qquad\:\:\:\:\:\:\:\: |\: -19,5 $
$ -8,5y=-25,5 \qquad\qquad\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\: | \: :(-8,5) $
$ \:\:\:\: $ $ \LARGE \longrightarrow $ $ \large y=3 $ $ \normalsize \:\:\: (IV) $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: (IV)\: in\: (III)\: ein: $
$ x=6,5-1,5\cdot (3) $
$ \:\:\:\: $ $ \LARGE \longrightarrow $ $ \large x=2 $
Die Lösungsmenge lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \mathbb{L}=\{(2|3)\} $
Graphische Darstellung$\qquad$ $ \large \textcolor{DodgerBlue}{ y_1=0,75x+1,5 } $ $\qquad$ $ \large \textcolor{OliveGreen}{ y_2=-0,\overline{6}x+4,\overline{3} } $
- Löse mit dem Gleichsetzungsverfahren:
$ \begin{cases} \begin{align*} \:\: &2x\:\: +\: 2,5y = 4 \\ \:\: &2x\:\: +\: 2y \:\:\:\:= 2 \end{align*} \end{cases} $
Lösung$ \begin{cases} \begin{align*} \:\: &2x\:\: +\: 2,5y = 4 \:\:\:\:\: (I)\\ \:\: &2x\:\: +\: 2y \:\:\:\:= 2 \:\:\:\:\: (II) \end{align*} \end{cases} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Stelle\: (I)\: und\: (II)\: nach\: 2x\: um: $
$ \begin{cases} 2x+2,5y &=4 \qquad |-2,5y \\ 2x+2y &=2 \qquad |-2y \end{cases} $ $ \qquad \Rightarrow \qquad $ $ \begin{cases} 2x=4-2,5y \qquad (I’) \\ 2x=2-2y \qquad\:\:\: (II’) \end{cases} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: (I’)\: und\: (II’)\: gleich: $
$ 2x=2x \:\: \leftrightarrow \:\: 4-2,5y=2-2y $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Fasse\: zusammen\: und\: stelle\: nach\: y\: um: $
$ 4-2,5y=2-2y \qquad |\: +2,5y $
$ 4=2+0,5y \qquad\qquad\: |\: -2 $
$ 2=0,5y \qquad\qquad\qquad |\: \cdot2 $
$ \:\:\:\: $ $ \LARGE \longrightarrow $ $ \large y=4 $ $ \normalsize \:\:\: (III) $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: (III)\: in\: (I’)\: oder\: (II’)\: ein: $
$ in\: (II’):\: 2x=2-2\cdot (4) $
$ \qquad\qquad\: 2x=-6 \qquad \: | :2 $
$ \:\:\:\: $ $ \LARGE \longrightarrow $ $ \large x=-3 $
Die Lösungsmenge lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \mathbb{L}=\{(-3|4)\} $
Graphische Darstellung$\qquad$ $ \large \textcolor{DodgerBlue}{ y_1=-0,8x+1,6 } $ $\qquad$ $ \large \textcolor{OliveGreen}{ y_2=-x+1 } $
$ \begin{cases} \begin{align*} \:\: 3x\:\: -\: 4y\:\: &=\:\: -6 \\ \:\: 2x\:\: +\: 3y\:\: &=\:\: 13 \end{align*} \end{cases} $
Lösung$ \begin{cases} \begin{align*} \:\: 3x\:\: -\: 4y\:\: &=\:\: -6 \:\: (I)\\ \:\: 2x\:\: +\: 3y\:\: &=\:\: 13 \:\:\: (II) \end{align*} \end{cases} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Form\: (I)\: und\: (II)\: gleich: $
$ \begin{cases} \begin{align*} \:\: 3x\:\: -\: 4y\:\: &=\:\: -6 \:\:\:\: |\: +4y \qquad\qquad (Rechne\: Plus\: 4y)\\ \:\: 2x\:\: +\: 3y\:\: &=\:\: 13 \:\:\:\:\: |\: -3y \qquad\qquad (Rechne\: Minus\: 3y) \end{align*} \end{cases} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Stelle\: nach\: x\: um: $
$ \begin{cases} \begin{align*} \:\: 3x\:\: &=\: -6\:\: +\:\: 4y \:\:\:\: |\: \cdot2 \qquad\qquad\:\:\:\: (Rechne\: Mal\: 2)\\ \:\: 2x\:\: &=\: 13\:\: -\:\: 3y \:\:\:\:\: |\: \cdot3 \qquad\qquad\:\:\:\: (Rechne\: Mal\: 3) \end{align*} \end{cases} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Gleiche\: die\: Variablen\: x\: aus: $
$ \begin{cases} \begin{align*} \:\: 6x\:\: &=\: -12\:\: +\:\: 8y \\ \:\: 6x\:\: &=\: 39\:\: -\:\: 9y \end{align*} \end{cases} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: die\: rechten\: Seiten\: gleich\: (6x=6x)\: und\: rechne\: nach\: y: $
$ 6x=6x $
$ \:\:\:\ \Leftrightarrow \:\:\:\: -12+8y=39-9y \qquad |\: +12\:/\: +9y\: (Rechne\: Plus\: 12\: und\: 9) $
$ \:\:\:\ \Leftrightarrow \qquad\:\:\:\:\:\: 17y=51 \qquad\qquad\: |\: :17\: (Teile\: durch\: 17) $
$ \:\:\:\: $ $ \LARGE \longrightarrow $ $ \large y=3 $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: y\: in\: (I)/(II)\: ein\: und\: rechne\: nach\: x: $
$ \:\:\:\: 3x-4\cdot (3)=-6\qquad |\: +12 $
$ \qquad\qquad\:\:\: 3x=6\qquad\:\:\: |\: :3 $
$ \:\:\:\: $ $ \LARGE \longrightarrow $ $ \large x=2 $
Die Lösungsmenge lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \mathbb{L}=\{(2|3)\} $
Graphische Darstellung$\qquad$ $ \large \textcolor{DodgerBlue}{ y_1=0,75x+1,5 } $ $\qquad$ $ \large \textcolor{OliveGreen}{ y_2=-0,\overline{6}x+4,\overline{3} } $
- Löse mit dem Gaußverfahren:
$ \begin{cases} 2x-3y=12 \\ 5x+2y=11 \end{cases} $
Lösung$ \large \begin{cases} 2x-3y=12 \\ 5x+2y=11 \end{cases} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Schreibe\: die\: Gleichungen\: in\: Matrixform um: $
$ \large \begin{bmatrix} \begin{array}{c c | c} 2&-3&12\\ 5&2&11 \end{array} \end{bmatrix} $ $ \large \begin{array}{l} l_1\\ l_2 \end{array} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \large Teile\: (l_1)\: durch\: 2:\: \textcolor{red}{\frac{l_1}{2}} $
$ \large \begin{bmatrix} \begin{array}{c c | c} \textcolor{red}{1} & -1,5 & 6\\ 5&2&11 \end{array} \end{bmatrix} $ $ \large \begin{array}{l} \textcolor{red}{l’_1}\\ l_2 \end{array} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \large \textcolor{red}{5\cdot l’_1-l_2} $
$ \large \begin{bmatrix} \begin{array}{c c | c} \textcolor{red}{1} & -1,5 & 6\\ 0& -9,5 &19 \end{array} \end{bmatrix} $ $ \large \begin{array}{l} \textcolor{red}{l’_1}\\ \textcolor{red}{l’_2} \end{array} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \large \textcolor{red}{\frac{l’_2}{-9,5}} $
$ \large \begin{bmatrix} \begin{array}{c c | c} \textcolor{red}{1} & -1,5 & 6\\ 0& \textcolor{red}{1} &-2 \end{array} \end{bmatrix} $ $ \large \begin{array}{l} \textcolor{red}{l’_1}\\ \textcolor{red}{l^{”}_2} \end{array} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \large \textcolor{red}{1,5\cdot l^{”}_2+l’_1} $
$ \large \begin{bmatrix} \begin{array}{c c | c} \textcolor{red}{1} & 0 & 3\\ 0& \textcolor{red}{1} &-2 \end{array} \end{bmatrix} $ $ \LARGE \leftrightarrow $ $ \begin{cases} x=3\\ y=-2 \end{cases} $
Die Lösungsmenge lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \mathbb{L}=\{(3|-2)\} $
$ \begin{cases} 5x-2y+3z &=19 \\ 2x+2y-4z &=-6\\ -2x+3y+z &=-12 \end{cases} $Lösung
$ \large \begin{cases} 5x-2y+3z &=19 \\ 2x+2y-4z &=-6\\ -2x+3y+z &=-12 \end{cases} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \large Bringe\: die\: Gleichungen\: in\: Matrixform: $
$ \large \begin{bmatrix} \begin{array}{c c c | c} 5&-2&3&19 \\ 2&2&-4&-6 \\ -2&3&1&-12 \end{array} \end{bmatrix} $ $ \large \begin{array}{l} l_1 \\ l_2 \\ l_3 \end{array} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \Large \textcolor{red}{\frac{l_1}{5}} $ $\:\:$$l_1$ wird durch 5 dividiert
$ \large \begin{bmatrix} \begin{array}{c c c | c} \textcolor{BurntOrange}{1} & \textcolor{red}{\frac{-2}{5}} & \textcolor{red}{\frac{3}{5}} & \textcolor{red}{\frac{19}{5}} \\ 2&2&-4&-6 \\ -2&3&1&-12 \end{array} \end{bmatrix} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \large \textcolor{red}{l_2-2\cdot l_1} $ $\:\:$Von $l_2$ wird subtrahiert 2⋅$l_1$
$ \large \begin{bmatrix} \begin{array}{c c c | c} \textcolor{BurntOrange}{1} & \frac{-2}{5} & \frac{3}{5} & \frac{19}{5} \\ \textcolor{red}{0} & \textcolor{red}{\frac{14}{5}} & \textcolor{red}{\frac{-26}{5}} & \textcolor{red}{\frac{-68}{5}} \\ -2&3&1&-12 \end{array} \end{bmatrix} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \large \textcolor{red}{l_3 – (-2\cdot l_1)} $ $\:\:$Von $l_3$ wird subtrahiert (-2⋅$l_1$)
$ \large \begin{bmatrix} \begin{array}{c c c | c} \textcolor{BurntOrange}{1} & \frac{-2}{5} & \frac{3}{5} & \frac{19}{5} \\ \textcolor{red}{0} & \frac{14}{5} & \frac{-26}{5} & \frac{-68}{5} \\ \textcolor{red}{0} & \textcolor{red}{\frac{11}{5}} & \textcolor{red}{\frac{11}{5}} & \textcolor{red}{\frac{-22}{5}} \end{array} \end{bmatrix} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \large \textcolor{red}{l_2:\frac{14}{5}} $ $\:\:$$l_2$ wird dividiert durch $\frac{14}{5}$
$ \large \begin{bmatrix} \begin{array}{c c c | c} \textcolor{BurntOrange}{1} & \frac{-2}{5} & \frac{3}{5} & \frac{19}{5} \\ \textcolor{red}{0} & \textcolor{BurntOrange}{1} & \textcolor{red}{\frac{-13}{7}} & \textcolor{red}{\frac{-34}{7}} \\ \textcolor{red}{0} & \textcolor{red}{\frac{11}{5}} & \textcolor{red}{\frac{11}{5}} & \textcolor{red}{\frac{-22}{5}} \end{array} \end{bmatrix} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \large \textcolor{red}{l_3 – (\frac{11}{5})\cdot l_2} $ $\:\:$Von $l_3$ wird subtrahiert $\frac{14}{5}\cdot l_2$
$ \large \begin{bmatrix} \begin{array}{c c c | c} \textcolor{BurntOrange}{1} & \frac{-2}{5} & \frac{3}{5} & \frac{19}{5} \\ \textcolor{red}{0} & \textcolor{BurntOrange}{1} & \frac{-13}{7} & \frac{-34}{7} \\ \textcolor{red}{0} & \textcolor{red}{0} & \textcolor{red}{\frac{44}{7}} & \textcolor{red}{\frac{44}{7}} \end{array} \end{bmatrix} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \large \textcolor{red}{l_3:(\frac{44}{7})} $ $\:\:$$l_3$ wird dividiert durch $\frac{44}{7}$
$ \large \begin{bmatrix} \begin{array}{c c c | c} \textcolor{BurntOrange}{1} & \frac{-2}{5} & \frac{3}{5} & \frac{19}{5} \\ \textcolor{red}{0} & \textcolor{BurntOrange}{1} & \frac{-13}{7} & \frac{-34}{7} \\ \textcolor{red}{0} & \textcolor{red}{0} & \textcolor{BurntOrange}{1} & \textcolor{BurntOrange}{1} \end{array} \end{bmatrix} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \large \textcolor{red}{l_2-(-\frac{13}{7})\cdot l_3} $ $\:\:$Von $l_2$ wird subtrahiert $(\frac{-13}{7})\cdot l_3$
$ \large \begin{bmatrix} \begin{array}{c c c | c} \textcolor{BurntOrange}{1} & \frac{-2}{5} & \frac{3}{5} & \frac{19}{5} \\ \textcolor{red}{0} & \textcolor{BurntOrange}{1} & \textcolor{red}{0} & \textcolor{red}{-3} \\ \textcolor{red}{0} & \textcolor{red}{0} & \textcolor{BurntOrange}{1} & \textcolor{BurntOrange}{1} \end{array} \end{bmatrix} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \large \textcolor{red}{l_1-(\frac{3}{5})\cdot l_3} $ $\:\:$Von $l_1$ wird subtrahiert $(\frac{3}{5})\cdot l_3$
$ \large \begin{bmatrix} \begin{array}{c c c | c} \textcolor{BurntOrange}{1} & \textcolor{red}{\frac{-2}{5}} & \textcolor{red}{0} & \textcolor{red}{\frac{16}{5}} \\ \textcolor{red}{0} & \textcolor{BurntOrange}{1} & \textcolor{red}{0} & \textcolor{red}{-3} \\ \textcolor{red}{0} & \textcolor{red}{0} & \textcolor{BurntOrange}{1} & \textcolor{BurntOrange}{1} \end{array} \end{bmatrix} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \large \textcolor{red}{l_1-(-\frac{2}{5})\cdot l_2} $ $\:\:$Von $l_1$ wird subtrahiert $(-\frac{2}{5})\cdot l_2$
$ \large \begin{bmatrix} \begin{array}{c c c | c} \textcolor{BurntOrange}{1} & \textcolor{red}{0} & \textcolor{red}{0} & \textcolor{black}{2} \\ \textcolor{red}{0} & \textcolor{BurntOrange}{1} & \textcolor{red}{0} & \textcolor{black}{-3} \\ \textcolor{red}{0} & \textcolor{red}{0} & \textcolor{BurntOrange}{1} & \textcolor{black}{1} \end{array} \end{bmatrix} $ $ \:\: \large \Longleftrightarrow \:\: \begin{cases} 1\cdot x + 0\cdot y + 0\cdot z=2 \\ 0\cdot x + 1\cdot y + 0\cdot z=-3 \\ 0\cdot x + 0\cdot y + 1\cdot z=1 \end{cases} $ $ \:\: \large \Rightarrow \:\: \begin{cases} x=2 \\ y=-3 \\ z=1 \end{cases} $
Die Lösungsmenge lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \mathbb{L}=\{(2|-3|1)\} $
- Löse mit Cramersche Regel oder Determinantenmethode:
$ \begin{cases} 5x-2y+3z &=19 \\ 2x+2y-4z &=-6\\ -2x+3y+z &=-12 \end{cases} $Lösung
$ \normalsize \begin{cases} 5x-2y+3z &=19 \\ 2x+2y-4z &=-6\\ -2x+3y+z &=-12 \end{cases} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Bringe\: die\: Gleichungen\: in\: Matrixform: $
$ \normalsize \begin{bmatrix} \begin{array}{c c c | c} 5&-2&3&19 \\ 2&2&-4&-6 \\ -2&3&1&-12 \end{array} \end{bmatrix} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Berechne\: die\: Determinante\: von\: A\: (det(A))/(Regel\: von\: Sarrus) $
$ \normalsize det(A)= \begin{vmatrix} \begin{array}{c c c} 5&-2&3 \\ 2&2&-4 \\ -2&3&1 \end{array} \end{vmatrix} $ $ \:\: $ $ \normalsize \begin{vmatrix} \begin{array}{c c c} 5&-2&3 \\ 2&2&-4 \\ -2&3&1 \end{array} \end{vmatrix} $
$\qquad\:\:\:\:\:\:$ $ = 5\cdot2\cdot1+(-2)\cdot(-4)\cdot(-2)+3\cdot2\cdot3-(-2)\cdot2\cdot3-3\cdot(-4)\cdot5-1\cdot2\cdot(-2) $
$\qquad\:\:\:\:\:\:$ $ =88 $
$\:\:$
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Berechne\: die\: det(A_1),\: det(A_2),\: und\: det(A_3) $
$ \normalsize det(A_1)= \begin{vmatrix} \begin{array}{c c c} \textcolor{red}{19} &-2&3 \\ \textcolor{red}{-6} &2&-4 \\ \textcolor{red}{-12} &3&1 \end{array} \end{vmatrix} $ $ \:\: $ $ \normalsize \begin{vmatrix} \begin{array}{c c c} 19&-2&3 \\ -6&2&-4 \\ -12&3&1 \end{array} \end{vmatrix} $
$\qquad\:\:\:\:\:\:$ $ =19\cdot2\cdot1+(-2)\cdot(-4)\cdot(-12)+3\cdot(-6)\cdot3-(-12)\cdot2\cdot3-3\cdot(-4)\cdot19-1\cdot(-6)\cdot(-2) $
$\qquad\:\:\:\:\:\:$ $ =176 $
$ \normalsize det(A_2)= \begin{vmatrix} \begin{array}{c c c} 5& \textcolor{red}{19} &3 \\ 2& \textcolor{red}{-6} &-4 \\ -2& \textcolor{red}{-12} &1 \end{array} \end{vmatrix} $ $ \:\: $ $ \normalsize \begin{vmatrix} \begin{array}{c c c} 5&19&3 \\ 2&-6&-4 \\ -2&-12&1 \end{array} \end{vmatrix} $
$\qquad\:\:\:\:\:\:$ $ = 5\cdot(-6)\cdot1+19\cdot(-4)\cdot(-2)+3\cdot2\cdot(-12)-(-2)\cdot(-6)\cdot3-(-12)\cdot(-4)\cdot5-1\cdot2\cdot19 $
$\qquad\:\:\:\:\:\:$ $ =-264 $
$ \normalsize det(A_3)= \begin{vmatrix} \begin{array}{c c c} 5&-2& \textcolor{red}{19} \\ 2&2& \textcolor{red}{-6} \\ -2&3& \textcolor{red}{-12} \end{array} \end{vmatrix} $ $ \:\: $ $ \normalsize \begin{vmatrix} \begin{array}{c c c} 5&-2&19 \\ 2&2&-6 \\ -2&3&-12 \end{array} \end{vmatrix} $
$\qquad\:\:\:\:\:\:$ $ = 5\cdot2\cdot(-12)+(-2)\cdot(-6)\cdot(-2)+ 19\cdot2\cdot3-(-2)\cdot2\cdot19-3\cdot(-6)\cdot5-(-12)\cdot2\cdot(-2) $
$\qquad\:\:\:\:\:\:$ $ =88 $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Bestimme\: die\: Lösung $
$ \qquad \normalsize det(A)=88 $
$ \qquad \normalsize det(A_1)=176 \qquad | \qquad det(A_2)=-264 \qquad | \qquad det(A_3)=88 $
$ \qquad\qquad \Large x=\frac{det(A_1)}{det(A)}=\frac{176}{88}=2 $
$ \qquad\qquad \Large y=\frac{det(A_2)}{det(A)}=\frac{-264}{88}=-3 $
$ \qquad\qquad \Large z=\frac{det(A_3)}{det(A)}=\frac{88}{88}=1 $
Die Lösungsmenge lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \mathbb{L}=\{(2|-3|1)\} $
$ \begin{cases} \begin{align*} \:\: x\:\: +\: 5y\:\: &=\:\: -6 \\ \:\: 2x\:\: +\: 4y\:\: &=\:\: 0 \end{align*} \end{cases} $
Lösung
$
\begin{cases}
\begin{align*}
\:\: x\:\: +\: 5y\:\: &=\:\: -6 \:\: (I)\\
\:\: 2x\:\: +\: 4y\:\: &=\:\: 0 \:\:\: (II)
\end{align*}
\end{cases}
$
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Stelle\: (I)\: nach\: x\: um: $
$ x+5y=-6 \qquad |-5y \:\:\:(Rechne\: Minus\: -5y) $
$ \:\:\:\: $ $ \LARGE \longrightarrow $ $ \large x=-6-5y $ $ \normalsize \:\:\: (III) $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: (III)\: in\: (II)\: ein: $
$ 2\cdot (-6-5y)+4y=0 $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Klammere\: auf\: und\: fasse\: zusammen\: nach\: y: $
$ 2\cdot (-6-5y)+4y=0 \qquad\qquad\qquad |\:Klammer\: auflösen $
$ -12-10y+4y=0 \qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\:\:\: |\:Zusammenfassen $
$ -12-6y=0 \qquad\qquad\qquad\qquad\:\:\:\:\:\:\:\: |\: +12 $
$ -6y=12 \qquad\qquad\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: | \: :(-6) $
$ \:\:\:\: $ $ \LARGE \longrightarrow $ $ \large y=-2 $ $ \normalsize \:\:\: (IV) $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: (IV)\: in\: (III)\: ein: $
$ x=-6-5\cdot (-2) $
$ \:\:\:\: $ $ \LARGE \longrightarrow $ $ \large x=4 $
Die Lösungsmenge lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \mathbb{L}=\{(4|-2)\} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Stelle\: (I)\: nach\: x\: um: $
$ x+5y=-6 \qquad |-5y \:\:\:(Rechne\: Minus\: -5y) $
$ \:\:\:\: $ $ \LARGE \longrightarrow $ $ \large x=-6-5y $ $ \normalsize \:\:\: (III) $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: (III)\: in\: (II)\: ein: $
$ 2\cdot (-6-5y)+4y=0 $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Klammere\: auf\: und\: fasse\: zusammen\: nach\: y: $
$ 2\cdot (-6-5y)+4y=0 \qquad\qquad\qquad |\:Klammer\: auflösen $
$ -12-10y+4y=0 \qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\:\:\: |\:Zusammenfassen $
$ -12-6y=0 \qquad\qquad\qquad\qquad\:\:\:\:\:\:\:\: |\: +12 $
$ -6y=12 \qquad\qquad\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: | \: :(-6) $
$ \:\:\:\: $ $ \LARGE \longrightarrow $ $ \large y=-2 $ $ \normalsize \:\:\: (IV) $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Setze\: (IV)\: in\: (III)\: ein: $
$ x=-6-5\cdot (-2) $
$ \:\:\:\: $ $ \LARGE \longrightarrow $ $ \large x=4 $
Die Lösungsmenge lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \mathbb{L}=\{(4|-2)\} $
Graphische Darstellung
$\qquad$
$
\large
\textcolor{DodgerBlue}{
y_1=-0,2x-1,2
}
$
$\qquad$
$
\large
\textcolor{OliveGreen}{
y_2=-0,5x
}
$
$ \begin{cases} 2x+3y+4z &=1,4 \\ 3x-2y-z &=1,2\\ 5x+4y+3z &=1,4 \end{cases} $
Lösung
$ \normalsize \begin{cases} 2x+3y+4z &=1,4 \\ 3x-2y-z &=1,2\\ 5x+4y+3z &=1,4 \end{cases} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Bringe\: die\: Gleichungen\: in\: Matrixform: $
$ \normalsize \begin{bmatrix} \begin{array}{c c c | c} 2&3&4&1,4 \\ 3&-2&-1&1,2 \\ 5&4&3&1,4 \end{array} \end{bmatrix} $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Determinante\: von\: A\: (det(A))\: mit\: dem\: Cofaktor\: Methode $
$ \normalsize det(A)= \begin{vmatrix} \begin{array}{c c c} \textcolor{DodgerBlue}{2} & \textcolor{OliveGreen}{3} & \textcolor{Orange}{4} \\ 3&-2&-1 \\ 5&4&3 \end{array} \end{vmatrix} $
$ \qquad\:\:\:\: \normalsize = \textcolor{red}{+} \: \textcolor{DodgerBlue}{2} \cdot \begin{vmatrix} \begin{array}{c c c} \textcolor{DodgerBlue}{-2} & \textcolor{DodgerBlue}{-1} \\ \textcolor{DodgerBlue}{4} & \textcolor{DodgerBlue}{3} \end{array} \end{vmatrix} $ $ \: \normalsize \textcolor{red}{—} \: $ $ \normalsize \textcolor{OliveGreen}{3} \cdot \begin{vmatrix} \begin{array}{c c c} \textcolor{OliveGreen}{3}& \textcolor{OliveGreen}{-1} \\ \textcolor{OliveGreen}{5}& \textcolor{OliveGreen}{3} \end{array} \end{vmatrix} $ $ \: \normalsize \textcolor{red}{+} \: $ $ \normalsize \textcolor{Orange}{4} \cdot \begin{vmatrix} \begin{array}{c c c} \textcolor{Orange}{3}& \textcolor{Orange}{-2} \\ \textcolor{Orange}{5}& \textcolor{Orange}{4} \end{array} \end{vmatrix} $
$ \qquad\:\:\:\: \normalsize = \textcolor{red}{+} \: \textcolor{DodgerBlue}{2}\cdot [\textcolor{DodgerBlue}{(-2)}\cdot \textcolor{DodgerBlue}{3} – \textcolor{DodgerBlue}{4}\cdot (\textcolor{DodgerBlue}{-1})] \textcolor{OliveGreen}{-} \textcolor{OliveGreen}{3}\cdot [\textcolor{OliveGreen}{3}\cdot \textcolor{OliveGreen}{3} – \textcolor{OliveGreen}{5}\cdot (\textcolor{OliveGreen}{-1})] \textcolor{Orange}{+} \textcolor{Orange}{4}\cdot [\textcolor{Orange}{3}\cdot \textcolor{Orange}{4} – \textcolor{Orange}{5}\cdot (\textcolor{Orange}{-2})] $
$ \qquad\:\:\:\: \normalsize \textcolor{black}{=} 42 $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Berechne\: die\: det(A_1),\: det(A_2),\: und\: det(A_3) $
$ \normalsize det(A_1)= \begin{vmatrix} \begin{array}{c c c} \textcolor{red}{1,4} &3&4 \\ \textcolor{red}{1,2} &-2&-1 \\ \textcolor{red}{1,4} &4&3 \end{array} \end{vmatrix} $
$ \qquad \normalsize = \textcolor{red}{+}1,4 \cdot \begin{vmatrix} -2&-1\\ 4&3 \end{vmatrix} \textcolor{red}{-}3 \cdot \begin{vmatrix} 1,2&-1\\ 1,4&3 \end{vmatrix} \textcolor{red}{+}4 \cdot \begin{vmatrix} 1,2&-2\\ 1,4&4 \end{vmatrix} $
$ \qquad \normalsize = 1,4\cdot [(-2)\cdot3 -4\cdot (-1)] – 3\cdot [1,2\cdot3 -1,4\cdot (-1)] + 4\cdot [1,2\cdot4 -1,4\cdot (-2)] $
$ \qquad \normalsize =12,6 $
$ \normalsize det(A_2)= \begin{vmatrix} \begin{array}{c c c} 2&\textcolor{red}{1,4} &4 \\ 3&\textcolor{red}{1,2} &-1 \\ 5&\textcolor{red}{1,4} &3 \end{array} \end{vmatrix} $
$ \qquad \normalsize = \textcolor{red}{+}2 \cdot \begin{vmatrix} 1,2&-1\\ 1,4&3 \end{vmatrix} \textcolor{red}{-}1,4 \cdot \begin{vmatrix} 3&-1\\ 5&3 \end{vmatrix} \textcolor{red}{+}4 \cdot \begin{vmatrix} 3&1,2\\ 5&1,4 \end{vmatrix} $
$ \qquad \normalsize = 2\cdot [1,2\cdot3 -1,4\cdot (-1)] – 1,4\cdot [3\cdot3 -5\cdot (-1)] + 4\cdot [3\cdot1,4 -5\cdot 1,2] $
$ \qquad \normalsize =-16,8 $
$ \normalsize det(A_3)= \begin{vmatrix} \begin{array}{c c c} 2&3&\textcolor{red}{1,4} \\ 3&-2&\textcolor{red}{1,2} \\ 5&4&\textcolor{red}{1,4} \end{array} \end{vmatrix} $
$ \qquad \normalsize = \textcolor{red}{+}2 \cdot \begin{vmatrix} -2&1,2\\ 4&1,4 \end{vmatrix} \textcolor{red}{-}3 \cdot \begin{vmatrix} 3&1,2\\ 5&1,4 \end{vmatrix} \textcolor{red}{+}1,4 \cdot \begin{vmatrix} 3&-2\\ 5&4 \end{vmatrix} $
$ \qquad \normalsize = 2\cdot [(-2)\cdot1,4 -4\cdot 1,2] – 3\cdot [3\cdot1,4 -5\cdot 1,2] + 1,4\cdot [3\cdot4 -5\cdot (-2)] $
$ \qquad \normalsize =21 $
$ \:\:\: $ $ \Large \Bigg\downarrow $ $ \normalsize Bestimme\: die\: Lösung $
$ \qquad \normalsize det(A)=42 $
$ \qquad \normalsize det(A_1)=12,6 \qquad | \qquad det(A_2)=-16,8 \qquad | \qquad det(A_3)=21 $
$ \qquad\qquad \large x=\frac{det(A_1)}{det(A)}=\frac{12,6}{42}=0,3 $
$ \qquad\qquad \large y=\frac{det(A_2)}{det(A)}=\frac{-16,8}{42}=-0,4 $
$ \qquad\qquad \large z=\frac{det(A_3)}{det(A)}=\frac{21}{42}=0,5 $
Die Lösungsmenge lautet:
$\qquad\qquad\qquad\qquad$ ➪ $\:\:$ $ \large \mathbb{L}=\{\frac{3}{10}|-\frac{2}{5}|\frac{1}{2})\} $
Rekonstruktion von Funktionen
Rekonstruktion von Funktionen
Bei der Rekonstruktion von Funktionen musst du anhand von gegebenen Informationen eine ganzrationale Funktionsgleichung bestimmen. Dazu stellst du Gleichungen auf, löse sie zur Bestimmung der rekonstruierte Funktion.
Funktionen rekonstruieren Vorgehen
- Schreibe die allgemeine Funktionsgleichung der gesuchten Funktionsart auf, und bestimme ihre Ableitungen.
$ \normalsize \textcolor{black}{ f(x)=ax^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + … + a_1x^1 + a_0x^0\:\: (x^0=1) } $
$ \normalsize \textcolor{black}{ \:\:\:f(x)=ax^4+bx^3+cx^2+dx+e } $ $\:\:\: \rightarrow\:\:$
$ \normalsize \textcolor{black}{ \:\:\:f(x)=ax^3+bx^2+cx+d } $ $\qquad\:\:\:\:\:\: \rightarrow\:\:$ -
Übersetze die gegebenen Informationen (Nullstelle , Tangente , …) aus der Rekonstruktion in Mathe Gleichungen.
$ \normalsize \textcolor{black}{ f(x)=ax^2+bx+c. } $
$ \qquad \normalsize \textcolor{black}{ \Longrightarrow 2=a(1)^2+b(1)+c } $ - Stelle ein lineares Gleichungssystem (LGS) auf und löse es.
- Bestimme deine rekonstruierte Funktion.
Beispielaufgabe: Rekonstruktion von Funktionen
Lösung
$ \qquad \large \textcolor{black}{ \begin{cases} f(x)=ax^3+bx^2+cx+d\\ f'(x)=3ax^2+2bx+c\\ f”(x)=6ax+2b \end{cases} } $
$\:\:\:\:$ $ \large (-1|2)\:\: \rightarrow f(-1)=2 $.
$\qquad$ $ \large \Leftrightarrow f(-1)=a\cdot(-1)^3+b\cdot(-1)^2+c\cdot(-1)+d=2 $
$\qquad$ $ \large \Leftrightarrow f(-1)=-a+b-c+d=2 $
$\:\:\:\:$ $ \large (-1|2)\:\: \rightarrow f'(-1)=0 $.
$\qquad$ $ \large \Leftrightarrow f'(-1)=3a\cdot (-1)^2+2b\cdot(-1)+c=0 $
$\qquad$ $ \large \Leftrightarrow f'(-1)=3a-2b+c=0 $
$\:\:\:\:$ $ \large x=1\:\: \rightarrow f”(1)=0 $.
$\qquad$ $ \large \Leftrightarrow f”(1)=6a\cdot 1+2b=0 $
$\qquad$ $ \large \Leftrightarrow f”(1)=6a+2b=0 $
$\:\:\:\:$ $ \qquad \large \:\: \rightarrow f'(2)=9 $.
$\qquad$ $ \large \Leftrightarrow f'(2)=3a\cdot 2^2+2b\cdot 2+c=9 $
$\qquad$ $ \large \Leftrightarrow f'(2)=12a+4b+c=9 $
$\qquad$
$\qquad$ $ \large \begin{cases} -a+b-c+d &=2 \:\:\: I\\ 3a-2b+c &=0 \:\:\: II\\ 6a+2b &=0 \:\:\: III\\ 12a+4b+c &=9 \:\:\: IV \end{cases} $
$\qquad$
$ \qquad\qquad \large II-IV \Rightarrow\:\: -9a-6b=-9\:\: V $
$ \qquad\qquad \large \textcolor{orange}{3}\cdot III + V \Rightarrow \begin{cases} \textcolor{orange}{18}a + \textcolor{orange}{6}b &= \textcolor{orange}{0} \\ -9a-6b &=-9 \\ \hline 9a &= -9 \qquad |\: :9 \end{cases} $
$ \qquad\qquad\qquad\qquad\qquad\qquad \Large \longrightarrow \underline{\textcolor{DodgerBlue}{a=-1}} $
$\qquad$
$ \qquad\qquad \large \Rightarrow\:\: 6(-1)+2b =0 \qquad|\: +6 \\ $
$ \qquad\qquad \large \Rightarrow\:\: 2b =6 \qquad\qquad \:\:\:\:\:\:\:\:|\: :2 \\ $
$ \qquad\qquad\qquad\qquad\qquad\qquad \Large \longrightarrow \underline{\textcolor{OliveGreen}{b=3}} $
$\qquad$
$ \qquad\qquad \large \Rightarrow\:\: 3(-1)-2(3)+c=0 $
$\qquad$
$ \qquad\qquad \large \Rightarrow\:\: -3-6+c=0 \qquad|\: +9 $
$ \qquad\qquad\qquad\qquad\qquad\qquad \Large \longrightarrow \underline{\textcolor{BurntOrange}{c=9}} $
$\qquad$
$ \qquad\qquad \large \Rightarrow\:\: -(-1)+3-9+d=2 $
$\qquad$
$ \qquad\qquad \large \Rightarrow\:\: 1+3-9+d=2 \qquad|\: +5 $
$ \qquad\qquad\qquad\qquad\qquad\qquad \Large \longrightarrow \underline{\textcolor{DarkOrchid}{d=7}} $
$\qquad$
$\qquad \qquad$ ➪ $ \Large f(x)=-x^3+3x^2+9x+7 $
Übungsaufgaben
Bestimme jeweils eine Funktion, die folgende Eigenschaften besitzt.
-
Eine Funktion 2. Grades, besitzt einen Schnittpunkt mit der $y$-Achse bei $(0|-3)$ und einen Hochpunkt bei $H(3|2)$
Lösung1. Allgemeine Funktionsgleichung und Ableitungen bestimmen
- Eine Funktion 2. Grades ist eine quadratische Funktion, der Form:
$ \qquad f(x)=ax^2+bx+c$, $\qquad a, b \:\:und\:\: c \in \mathbb{R} $ - Die 1. und 2. Ableitungen sind:
$ \qquad f'(x)=2ax+b $
$ \qquad f”(x)=2a $
2. Informationen in Mathe Gleichungen übersetzen
$\:\:\:\:$ I. Der Schnittpunkt mit der $y$-Achse $S_y(0|-3) \rightarrow f(0)=-3$
$ \qquad \Leftrightarrow f(0)=a(0)^2+b(0)+c=-3 $
$ \qquad \longrightarrow {c=-3}\:\:\: \textcolor{red}{(I)} $
$\:\:\:\:$ II. Der Graph hat ein Hochpunkt beit $H(3|2) \rightarrow f(3)=2$
$ \qquad \Leftrightarrow a\cdot 3^2+b\cdot 3+c=2 $
$ \qquad \Leftrightarrow 9a+3b+c=2\:\:\: \textcolor{red}{(II)} $
$\:\:\:\:$ III. Der Graph hat ein Hochpunkt beit $H(3|2) \rightarrow f'(3)=0$
$ \qquad \Leftrightarrow 2a\cdot 3+b=0 $
$ \qquad \Leftrightarrow 6a+b=0\:\:\: \textcolor{red}{(III)} $
3. Lineares Gleichungssystem (LGS) auftellen und lösen
$ \qquad \begin{cases} \begin{align*} c &=-3 \:\:\: \textcolor{red}{(I)}\\ 9a + 3b + c &=2 \:\:\:\:\: \textcolor{red}{(II)}\\ 6a + b &=0 \:\:\:\: \textcolor{red}{(III)} \end{align*} \end{cases} $
$\:\:\:$ Setze $I$ in $II$
$ \qquad \Rightarrow 9a+3b-3=2\:\:|\:\:+3 $
$ \qquad \Leftrightarrow 9a+3b-3=5\:\:\: \textcolor{red}{(IV)} $
$ \qquad -3\cdot III+IV \Rightarrow \begin{cases} \begin{align*} (6a+b &=0)\cdot(-3)\\ 9a+3b &=5 \end{align*} \end{cases} $ $ \:\: \Rightarrow \:\: \begin{cases} \begin{align*} -18a-3b &=0\\ 9a+3b &=5\\ \hline -9a &=5 \:\:\: |\: (-9) \end{align*} \end{cases} $
$ \qquad\qquad\qquad\qquad\qquad \qquad\qquad\qquad\qquad\qquad \qquad\:\:\:\:\: \large \longrightarrow a=-\frac{5}{9} $
$\:\:\:$ Setze $a$ in $III$ ein: $\Rightarrow 6(-\frac{5}{9})+b=0 \:\:\:| \: +\frac{30}{9}$
$ \qquad\qquad\qquad\qquad\qquad\qquad\: \large \longrightarrow b=\frac{30}{9}=\frac{10}{3} $
4. Rekonstruierte Funktion bestimmen
$\:\:\:$ Die allgemeine Funktionsgleichung lautet:
$\qquad$ ➪ $ \large f(x)=-\frac{5}{9}x^2+ \frac{10}{3}x-3 $
Graphische Darstellung$ \large f(x)=-\frac{5}{9}x^2+ \frac{10}{3}x-3 $
- Eine Funktion 2. Grades ist eine quadratische Funktion, der Form:
-
Die Funktion ist vom Grad 3, besitzt eine doppelte Nullstelle bei $x_{1,2}=-2$, eine einfache Nullstelle bei $x_3=0$ und verläuft durch den Punkt $P(-1|-2).$
LösungAllg. Funktionsgleichung bestimmen. Beispielaufage
- Eine Funktion 3. Grades ist eine Polynomfunktion, der Form:
$ \qquad f(x)=ax^3+bx^2+cx+d. $
Die Nullstellenform lautet:
$ f(x)=a\cdot (x-x_1)(x-x_2)(x-x_3) $
Die Funktion besitzt eine doppelte Nullstelle bei $ \large \textcolor{DodgerBlue}{x_{1,2}=-2} $ und eine Nullstelle bei $ \large \textcolor{OliveGreen}{x_3=0} $
Übersetze:
$ \qquad \large \longrightarrow f(x)=a\cdot (x-\textcolor{DodgerBlue}{2})(x-\textcolor{DodgerBlue}{2})(x-\textcolor{OliveGreen}{0}) $
Die Funktion verläuft durch den Punkt $P(-1|-2)$
$ \qquad \Rightarrow f(-1)=-2\:\: \Leftrightarrow \:\:a\cdot (-1+2)(-1+2)(-1-0)=-2 $
Klammer auf und fasse zusammen:
$ \qquad \Rightarrow\:\: a\cdot 1\cdot (-1)=-2 $
$ \qquad \large \iff \:\: a=2 $
Nun lautet die Funktionsgleichung (Funktionsterm):
$ \qquad f(x)= 2\cdot (x+2)(x+2)(x-0), $
Multipliziere die Klammern aus und bringe die Funktion in die allgemeine Form:
$ \qquad f(x)= 2\cdot (x^2+4x+4) $
$ \qquad = 2x^3+8x^2+8x $
Die Funktionsgleichung lautet:
$\qquad$ ➪ $ \large f(x)=2x^3+8x^2+8x $
Graphische Darstellung$ \:\:\: \large f(x)=2x^3+8x^2+8x $
- Eine Funktion 3. Grades ist eine Polynomfunktion, der Form:
-
Die Funktion ist vom Grad 3, punktsymmetrisch und verläuft durch die Punkte $P(1|-1,5).$ und $Q(3|7,5)$.
LösungAllg. Funktionsgleichung bestimmen. Beispielaufage
- Eine Funktion 3. Grades ist eine Polynomfunktion, der Form:
$ \qquad f(x)=ax^3+bx^2+cx+d. $
Da die Funktion punktsymmetrisch ist, entfallen alle Potenzen mit gerade Exponenten:
$\qquad \longrightarrow f(x)=ax^3+cx $
Die Punkte $P(1|-1,5)$ und $Q(3|7,5)$ liegen auf f:
Bedeutet:
$\qquad$ – Setze $P(1|-1,5)$ in die Gleichung ein:
$ \qquad\qquad \Rightarrow a\cdot 1^3+c\cdot 1=-1,5 $
$ \qquad\qquad \Leftrightarrow a+c=-1,5\:\:\: (I) $
$\qquad$ – Setze $Q(3|7,5)$ in die Gleichung ein:
$ \qquad\qquad \Rightarrow a\cdot 3^3+c\cdot 3=7,5 $
$ \qquad\qquad \Leftrightarrow 27a+3c=7,5\:\:\: | \textcolor{red}{:3} $
$ \qquad\qquad \rightarrow 9a+c=2,5\:\:\: (II) $
Stelle ein Lineares Gleichungssystem auf und löse es:
$ \qquad \qquad \begin{align*} \begin{cases} a+c &=-1,5 \:\:\: (I) \\ 9a+c &=2,5 \:\:\:\:\:\: (II) \end{cases} \end{align*} $
$\qquad \qquad (I)-(II)\:\: \Rightarrow \:\: -8a=-4\:\:\:|\: \textcolor{red}{:(-8)} $
$\qquad \qquad \qquad \qquad\:\:\:\:\:\: \large \rightarrow \:\: a=\frac{1}{2} $
$\qquad$ Setze $a$ in $(I)$ ein:
$ \qquad \qquad \qquad \qquad\:\:\: \Rightarrow\:\: \frac{1}{2}+c=-1,5\:\:\: |\: \textcolor{red}{-0,5} $
$\qquad \qquad \qquad \qquad\:\:\:\:\:\: \large \rightarrow \:\: c=-2 $
Die Funktionsgleichung lautet:
$\qquad\qquad$ ➪ $ \large f(x)=\frac{1}{2}x^3-2x. $
Graphische Darstellung$ \qquad \large f(x)=\frac{1}{2}x^3-2x $
Punktsymmetrie: $ \Large \textcolor{DodgerBlue}{f(-x)}= \textcolor{OliveGreen}{-f(x)} $
- Eine Funktion 3. Grades ist eine Polynomfunktion, der Form:
-
Die Funktion ist vom Grad 4 und achsensymmetrisch, besitzt eine doppelte Nullstelle bei $x_{1,2}=1$ und geht durch den Punkt $P(0|3)$.
LösungAllg. Funktionsgleichung bestimmen. Beispielaufage
- Eine Funktion 4. Grades ist eine Polynomfunktion, der Form:
$ \qquad f(x)=ax^4+bx^3+cx^2+dx+e. $
und dir Nullstellenform: $f(x)=a\cdot (x-x_1)(x-x_2)(x-x_3)(x-x_4)$
Die Funktion besitzt eine doppelte Nullstelle bei $x_{1,2}=1$ und weil achsensymmetrisch,
hat sie ebenfalls eine doppelte Nullstelle bei $x_{3,4}=-1$.
Das heißt, die Nullstellenform ist:
$ \qquad f(x)=a\cdot (x-1)(x-1)(x+1)(x+1) $
Der Punkte $P(0|3)$ liegt auf f:
Bedeutet:
$\qquad$ Setze $P(0|3)$ in die Gleichung ein und löse nach $a$:
$\qquad$ $a\cdot (x-1)(x-1)(x+1)(x+1)=3 $
Klammer auf und fasse zusammen:
$\qquad a\cdot (-1)(-1)\cdot 1 \cdot 1=3 $
Stelle nun den Funktionsterm auf:
$ \Large \downarrow $ Multipliziere die Klammern aus und bringe die Funktion in die allgemeine Form.
$ f(x)=3\cdot (x-1)(x+1)\cdot (x-1)(x+1) $
$ \Large \downarrow $ Benutze die 3. binomische Formel.
$ \qquad \Rightarrow f(x)=3\cdot (x^2-1)\cdot (x^2-1) $
$ \qquad \Rightarrow f(x)=3\cdot (x^4-2x^2+1) $
$ \qquad \Leftrightarrow f(x)=3x^4-6x^2+3 $
Die Funktionsgleichung lautet:
$\qquad\qquad$ ➪ $ \large f(x)=3x^4-6x^2+3. $
Graphische Darstellung$ \qquad \large f(x)=3x^4-6x^2+3. $
- Eine Funktion 4. Grades ist eine Polynomfunktion, der Form:
Weitere Aufgaben
Aufgaben mit nichtrationalen Funktionen
- Bestimme eine Exponentialfunktion der Form $f(x)=a^x+b$, welche durch die Punkte $P(1|4)$ und $Q(-1|\frac{4}{3})$ geht.
Lösung
Setze die gegebenen Punkte in die Funktionsgleichung ein:
$\:\:\:$ Für $P$ $\Rightarrow\:a^1+b=4$
$\:\:\:$ Für $Q$ $\Rightarrow\:a^{-1}+b=\frac{4}{3}$
Löse das Gleichungssystem:
$ \qquad \begin{cases} \begin{align*} a+b &=4 \:\:\:\: (I)\\ a^{-1}+b &=\frac{4}{3} \:\: (II) \end{align*} \end{cases} $
Subtrahiere die Gleichungen:
$\qquad (I)-(II) \: \Rightarrow\: a-a^{-1}=4-\frac{4}{3}$
Fasse zusammen und mache Gleichnahmig:
$\qquad \large \iff a-\frac{1}{a}=\frac{8}{3} \iff \frac{3\cdot a^2}{3a}- \frac{3\cdot 1}{3a}-\frac{8\cdot a}{3a}=0 $
$\qquad \Rightarrow 3a^2-8a-3=0\:\: |\: :3 $
$\qquad \Rightarrow a^2-2,66a-1=0 $
Löse mit pq-Formel oder andere Formeln:
$\qquad$ Mit pq-Formel: $a^2-2,66a-1=0$, mit $p=-2,66$ und $q=-1$.
Die 2 Lösungen sind:
$\qquad$ $ \large a_{1/2}=-\frac{p}{2} \pm \sqrt{(\frac{p}{2})^2-q} $
Setze $p$ und $q$ ein:
$\qquad$ $ \longrightarrow \begin{cases} a_1=2,99\approx3\\ oder\\ a_2=-0,33 \:\: \textcolor{red}{\longrightarrow (entfällt\: bei\: Exponentialfunktionen)} \end{cases} $
$\qquad$ $ \Rightarrow $ die Lösung ist $ \large \underline {a=3} $
Setze $a=3$ in Gleichung $(I)$ ein:
$\qquad$ $ \Rightarrow 3+b=4\:\:|\: (-3) $
$\qquad$ $ \iff \large \underline{b=1} $
Die gesuchte Funktionsgleichung lautet dann also:
$\qquad$ ➪ $ \large f(x)=3^x+1 $
Graphische Darstellung
$ \large f(x)=3^x+1 $
-
Gesucht ist eine Funktion der Form $f(x)=log_a x$. Die Funktion geht durch den Punkt $P(8|1,5)$.
Ermittle die Funktionsgleichung.
Lösung
Setze $P$ in die Funktion $f$ ein und löse nach a auf:
$\qquad$ $ 1,5=log_a\:8 $
$\qquad \:\:\:\:\:\:$ $ \Huge \downarrow $ Nach Logarithmusgesetze:
$\qquad$ $ \large a^{1,5}=8 $
$\qquad \:\:\:\:\:\:$ $ \Huge \downarrow $ Schreibe den Exponenten rationale um:
$\qquad$ $ \large a^{\frac{3}{2}}=8 $
$\qquad \:\:\:\:\:\:$ $ \Huge \downarrow $ Es gilt nach dem dritten Potenzgesetz:
$\qquad$ $ \large (a^3)^{\frac{1}{2}}=8 \:\:\:\:|\:\:\:\: \frac{3}{2} \equiv 3\cdot \frac{1}{2} $
$\qquad \:\:\:\:\:\:$ $ \Huge \downarrow $ oder auch:
$\qquad$ $ \large \sqrt{a^3}=8 $
$\qquad \:\:\:\:\:\:$ $ \Huge \downarrow $ Quadriere $(…)^2$:
$\qquad$ $ \large a^3=64 $
$\qquad \:\:\:\:\:\:$ $ \Huge \downarrow $ Ziehe die dritte Wurzel $\sqrt[3]{{…}}$:
$\qquad$ $ \large a=4 $
$\qquad \:\:\:\:\:\:$ $ \Huge \downarrow $
Damit lautet die Basis Funktionsgleichung:
$\qquad$ ➪ $ \large f(x)=log_4\:x $
Graphische Darstellung
$ \large f(x)=log_4\:x $
Lagebeziehungen von zwei Ebenen
Lagebeziehungen von zwei Ebenen
Ebenen können auf unterschiedliche Weise im Raum zueinander liegen. Die verschiedenen Optionen sind wie folgt:
Mögliche Lagebeziehungen zwischen zwei Ebenen
| Ebenen identisch | Jeder Punkt, der auf einer Ebene liegt, liegt auch auf der anderen und es gibt unendlich viele Schnittgeraden. |
|---|---|
| Ebenen schnittpunkt | Ebenen haben genau eine gemeinsame Schnittgerade, die alle Punkte enthält, die auf beiden Ebenen liegen. |
| Ebenen echt parallel | Zwei Geraden sind echt parallel, wenn sie durch eine Verschiebung identisch werden. |
Beispielaufgaben: Schnittgerade
Es gibt zwei Ebenen $G$ (in Koordinatenform) und $H$ (in Parameterform):
$ \qquad G:7x+y-3z-8=0 \:\:$ und $\:\: H:\vec{x}=\begin{pmatrix}0\\1\\0 \end{pmatrix} + r\cdot \begin{pmatrix}0\\-1\\2 \end{pmatrix} + s\cdot \begin{pmatrix}1\\0\\0 \end{pmatrix} $
Setze $H$ in $G$ ein:
$ \qquad G:7(0+r\cdot0+s\cdot1)+(1+r\cdot(-1)+s\cdot0)-3(0+r\cdot2+s\cdot0)-8=0 $
$ \qquad\qquad \Rightarrow 7s+1-r-6r-8=0 $
$ \qquad\qquad \Rightarrow 7s-7r-7-8=0\:\:|\: +7r $
$ \qquad\qquad \Rightarrow 7s-7=7r\:\:|\: :7 $
$ \qquad\qquad \iff \underline{s-1=r} $
Setze $r$ in $H$ ein um die Gleichung der Schnittgeraden $g$ zu erhalten:
$ \qquad\qquad g:\vec{x}=\begin{pmatrix}0\\1\\0 \end{pmatrix} + (s-1)\cdot \begin{pmatrix}0\\-1\\2 \end{pmatrix} + s\cdot \begin{pmatrix}1\\0\\0 \end{pmatrix} $
Fasse zusammen:
$ \qquad\qquad g:\vec{x}=\begin{pmatrix}0\\1\\0 \end{pmatrix} + s\cdot \begin{pmatrix}0\\-1\\2 \end{pmatrix} + (-1)\cdot \begin{pmatrix}0\\-1\\2 \end{pmatrix} + s\cdot \begin{pmatrix}1\\0\\0 \end{pmatrix} $
$ \qquad\qquad g:\vec{x}=\begin{pmatrix}0\\1\\0 \end{pmatrix} + (-1)\cdot \begin{pmatrix}0\\-1\\2 \end{pmatrix} + s\cdot \begin{pmatrix}0\\-1\\2 \end{pmatrix} + s\cdot \begin{pmatrix}1\\0\\0 \end{pmatrix} $
$ \qquad\qquad \iff g:\vec{x}=\begin{pmatrix}0\\2\\-2 \end{pmatrix} + \cdot \begin{pmatrix}1\\-1\\2 \end{pmatrix} $
$ \qquad\qquad \iff g:\vec{x}=\begin{pmatrix}0\\2\\-2 \end{pmatrix} + \cdot \begin{pmatrix}1\\-1\\2 \end{pmatrix} $
Die Schnittgerade lautet:
$ \qquad\qquad g:\vec{x}=\begin{pmatrix}0\\2\\-2 \end{pmatrix} + \cdot \begin{pmatrix}1\\-1\\2 \end{pmatrix} $
Übungsaufgaben
Bestimme die Schnittgerade der in Parameter- und Koordinatenform gegebenen Ebenen.
-
$\:\:\:
\large
\textcolor{black}{
E_1:-x+2y+z=-4
}$
$\qquad$
$\qquad$
$
\large
\textcolor{black}{
E_2: \vec{x}= \begin{pmatrix}2\\0\\-1 \end{pmatrix}
+
r\cdot \begin{pmatrix}0\\1\\-2 \end{pmatrix}
+
s\cdot \begin{pmatrix}2\\-1\\3 \end{pmatrix}}
$
Lösung
Lineare Unabhängigkeit
$\qquad \textcolor{black}{ E_1:-x+2y+z=-4; }$ $\qquad$ $ \textcolor{black}{ E_2: \vec{x}= \begin{pmatrix}2\\0\\-1 \end{pmatrix} + r\cdot \begin{pmatrix}0\\1\\-2 \end{pmatrix} + s\cdot \begin{pmatrix}2\\-1\\3 \end{pmatrix}} $
$ \qquad E_1:-(2+0\cdot r+2\cdot s) + 2(0+1\cdot r-1\cdot s) + (-1-2\cdot r+3\cdot s) =-4 $
$ \qquad\qquad \Rightarrow -2-2s+2r-2s-1-2r+3s=-4 \:\:|\:\:+3 $
$ \qquad\qquad \Rightarrow -s=-1 \:\:|\:\::(-1) $
$ \qquad\qquad \Longrightarrow \underline{s=1} $
Setze in $E_2$ ein um die Gleichung der Schnittgeraden zu erhalten:
$ \qquad g:\vec{x} = \begin{pmatrix}2\\0\\-1\end{pmatrix} + r\cdot \begin{pmatrix}0\\1\\-2\end{pmatrix} + 1\cdot \begin{pmatrix}2\\-1\\3\end{pmatrix} $
Fasse zusammen:
$ \qquad g:\vec{x} = \begin{pmatrix}2\\0\\-1\end{pmatrix} + 1\cdot \begin{pmatrix}2\\-1\\3\end{pmatrix} + r\cdot \begin{pmatrix}0\\1\\-2\end{pmatrix} $
$ \qquad \iff g:\vec{x} = \begin{pmatrix}4\\-1\\2\end{pmatrix} + r\cdot \begin{pmatrix}0\\1\\-2\end{pmatrix} $
Die Schnittgerade lautet:
$ \qquad\qquad\qquad\qquad g:\vec{x} = \begin{pmatrix}4\\-1\\2\end{pmatrix} + r\cdot \begin{pmatrix}0\\1\\-2\end{pmatrix} $
$ \textcolor{blue}{E_1} \cap \textcolor{purple}{E_2}=g $
$\qquad \textcolor{black}{ E_1:-x+2y+z=-4; }$ $\qquad$ $ \textcolor{black}{ E_2: \vec{x}= \begin{pmatrix}2\\0\\-1 \end{pmatrix} + r\cdot \begin{pmatrix}0\\1\\-2 \end{pmatrix} + s\cdot \begin{pmatrix}2\\-1\\3 \end{pmatrix}} $
$ \qquad E_1:-(2+0\cdot r+2\cdot s) + 2(0+1\cdot r-1\cdot s) + (-1-2\cdot r+3\cdot s) =-4 $
$ \qquad\qquad \Rightarrow -2-2s+2r-2s-1-2r+3s=-4 \:\:|\:\:+3 $
$ \qquad\qquad \Rightarrow -s=-1 \:\:|\:\::(-1) $
$ \qquad\qquad \Longrightarrow \underline{s=1} $
Setze in $E_2$ ein um die Gleichung der Schnittgeraden zu erhalten:
$ \qquad g:\vec{x} = \begin{pmatrix}2\\0\\-1\end{pmatrix} + r\cdot \begin{pmatrix}0\\1\\-2\end{pmatrix} + 1\cdot \begin{pmatrix}2\\-1\\3\end{pmatrix} $
Fasse zusammen:
$ \qquad g:\vec{x} = \begin{pmatrix}2\\0\\-1\end{pmatrix} + 1\cdot \begin{pmatrix}2\\-1\\3\end{pmatrix} + r\cdot \begin{pmatrix}0\\1\\-2\end{pmatrix} $
$ \qquad \iff g:\vec{x} = \begin{pmatrix}4\\-1\\2\end{pmatrix} + r\cdot \begin{pmatrix}0\\1\\-2\end{pmatrix} $
Die Schnittgerade lautet:
$ \qquad\qquad\qquad\qquad g:\vec{x} = \begin{pmatrix}4\\-1\\2\end{pmatrix} + r\cdot \begin{pmatrix}0\\1\\-2\end{pmatrix} $
Graphische Darstellung
$ \textcolor{blue}{E_1} \cap \textcolor{purple}{E_2}=g $
$\:\:\: \large \textcolor{black}{ E_1:x+2y-2z=5 }$ $\qquad$ $\qquad$ $ \large \textcolor{black}{ E_2: \vec{x}= \begin{pmatrix}7\\1\\2 \end{pmatrix} + r\cdot \begin{pmatrix}4\\1\\3 \end{pmatrix} + s\cdot \begin{pmatrix}2\\-1\\0 \end{pmatrix}} $
Lösung
Lagebestimmung
$\qquad \textcolor{black}{ E_1:x+2y-2z=5; }$ $\qquad$ $ \textcolor{black}{ E_2: \vec{x}= \begin{pmatrix}7\\1\\2 \end{pmatrix} + r\cdot \begin{pmatrix}4\\1\\3 \end{pmatrix} + s\cdot \begin{pmatrix}2\\-1\\0 \end{pmatrix}} $
$ \qquad E_1:(7+4\cdot r+2\cdot s) + 2\cdot (1+1\cdot r-1\cdot s) – 2\cdot (2+3\cdot r+0\cdot s) =5 $
$ \qquad\qquad \Rightarrow 7+4r+2s+2+2r-2s-4-6r=5 \:\: \iff 5=5\:\: W.A. $
Die Ebenen sind identisch, also liegen aufeinander.
$ \textcolor{blue}{E_1} \equiv \textcolor{purple}{E_2} $
$\qquad \textcolor{black}{ E_1:x+2y-2z=5; }$ $\qquad$ $ \textcolor{black}{ E_2: \vec{x}= \begin{pmatrix}7\\1\\2 \end{pmatrix} + r\cdot \begin{pmatrix}4\\1\\3 \end{pmatrix} + s\cdot \begin{pmatrix}2\\-1\\0 \end{pmatrix}} $
$ \qquad E_1:(7+4\cdot r+2\cdot s) + 2\cdot (1+1\cdot r-1\cdot s) – 2\cdot (2+3\cdot r+0\cdot s) =5 $
$ \qquad\qquad \Rightarrow 7+4r+2s+2+2r-2s-4-6r=5 \:\: \iff 5=5\:\: W.A. $
Die Ebenen sind identisch, also liegen aufeinander.
Graphische Darstellung
$ \textcolor{blue}{E_1} \equiv \textcolor{purple}{E_2} $
$\:\:\: \large \textcolor{black}{ E_1:\vec{x} = \begin{pmatrix}1\\1\\2 \end{pmatrix} + r\cdot \begin{pmatrix}0\\1\\1 \end{pmatrix} + s\cdot \begin{pmatrix}1\\1\\3 \end{pmatrix} } $ $\qquad$ $\qquad$ $ \large \textcolor{black}{ E_2:2x+y-z-1=0 } $
Lösung
Lagebestimmung
$ \qquad \textcolor{black}{ E_1: \vec{x}= \begin{pmatrix}1\\1\\2 \end{pmatrix} + r\cdot \begin{pmatrix}0\\1\\1 \end{pmatrix} + s\cdot \begin{pmatrix}1\\1\\3 \end{pmatrix}}; $ $\qquad$ $ \textcolor{black}{ E_2:2x+y-z-1=0 }$
$ \qquad\qquad \Rightarrow E_1: 2(1+0\cdot r+1\cdot s)+1+1\cdot r+1\cdot s-2-1\cdot r-3\cdot s-1=0 $
$ \qquad\qquad \iff E_1: 0=0 \:\:\: $
Die beiden Ebenen sind identisch, also liegen aufeinander.
$ \textcolor{dodgerblue}{E_1} \equiv \textcolor{purple}{E_2} $
$ \qquad \textcolor{black}{ E_1: \vec{x}= \begin{pmatrix}1\\1\\2 \end{pmatrix} + r\cdot \begin{pmatrix}0\\1\\1 \end{pmatrix} + s\cdot \begin{pmatrix}1\\1\\3 \end{pmatrix}}; $ $\qquad$ $ \textcolor{black}{ E_2:2x+y-z-1=0 }$
$ \qquad\qquad \Rightarrow E_1: 2(1+0\cdot r+1\cdot s)+1+1\cdot r+1\cdot s-2-1\cdot r-3\cdot s-1=0 $
$ \qquad\qquad \iff E_1: 0=0 \:\:\: $
Die beiden Ebenen sind identisch, also liegen aufeinander.
Graphische Darstellung
$ \textcolor{dodgerblue}{E_1} \equiv \textcolor{purple}{E_2} $
$\:\:\: \large \textcolor{black}{ E_1:\vec{x} = \begin{pmatrix}1\\-1\\3 \end{pmatrix} + r\cdot \begin{pmatrix}1\\-1\\-1 \end{pmatrix} + s\cdot \begin{pmatrix}-1\\2\\-1 \end{pmatrix} } $ $\qquad$ $\qquad$ $ \large \textcolor{black}{ E_2:x-2y+z-2=0 } $
Lösung
Lagebestimmung
$ \qquad \textcolor{black}{ E_1: \vec{x}= \begin{pmatrix}1\\-1\\3 \end{pmatrix} + r\cdot \begin{pmatrix}1\\-1\\-1 \end{pmatrix} + s\cdot \begin{pmatrix}-1\\2\\-1 \end{pmatrix}}; $ $\qquad$ $ \textcolor{black}{ E_2:x-2y+z-2=0 }$
$ \qquad \Rightarrow E_1: (1+1\cdot r+(-1)\cdot s) – 2[(-1)+(-1)\cdot r+2\cdot s] + 3+ (-1)\cdot r+ (-1)\cdot s – 2=0 $
Löse die Klammern auf und fasse zusammen:
$ \qquad \Rightarrow E_1: 1+r-s + 2+2r-4s + 3-r-s – 2=0 $
$ \qquad \Rightarrow r=-2+3s $
Setze $r$ in $E_1$ ein und fasse zusammen, um die ie Schnittgerade zu erhalten:
$\qquad$ $ \textcolor{black}{ E_1: \vec{x}= \begin{pmatrix}1\\-1\\3 \end{pmatrix} + (-2+3s)\cdot \begin{pmatrix}1\\-1\\-1 \end{pmatrix} + s\cdot \begin{pmatrix}-1\\2\\-1 \end{pmatrix}} $
$\qquad$ $ \textcolor{black}{ g: \vec{x}= \begin{pmatrix}1\\-1\\3 \end{pmatrix} – 2\cdot \begin{pmatrix}1\\-1\\-1 \end{pmatrix} + 3s\cdot \begin{pmatrix}1\\-1\\-1 \end{pmatrix} + s\cdot \begin{pmatrix}-1\\2\\-1 \end{pmatrix}} $
$ \qquad \textcolor{black}{ g: \vec{x}= \begin{pmatrix}-1\\1\\5 \end{pmatrix} + s\cdot \begin{pmatrix}2\\-1\\-4 \end{pmatrix}} $
$ \qquad \textcolor{black}{ \iff g: \vec{x}= \begin{pmatrix}-1\\1\\5 \end{pmatrix} + s\cdot \begin{pmatrix}2\\-1\\-4 \end{pmatrix}} $
Die Schnittgerade lautet:
$ \qquad\qquad\qquad\qquad\qquad \textcolor{black}{ \iff g: \vec{x}= \begin{pmatrix}-1\\1\\5 \end{pmatrix} + s\cdot \begin{pmatrix}2\\-1\\-4 \end{pmatrix}} $
$\textcolor{dodgerblue}{E_1} \cap \textcolor{magenta}{E_2}=$
$ \qquad \textcolor{black}{ E_1: \vec{x}= \begin{pmatrix}1\\-1\\3 \end{pmatrix} + r\cdot \begin{pmatrix}1\\-1\\-1 \end{pmatrix} + s\cdot \begin{pmatrix}-1\\2\\-1 \end{pmatrix}}; $ $\qquad$ $ \textcolor{black}{ E_2:x-2y+z-2=0 }$
$ \qquad \Rightarrow E_1: (1+1\cdot r+(-1)\cdot s) – 2[(-1)+(-1)\cdot r+2\cdot s] + 3+ (-1)\cdot r+ (-1)\cdot s – 2=0 $
Löse die Klammern auf und fasse zusammen:
$ \qquad \Rightarrow E_1: 1+r-s + 2+2r-4s + 3-r-s – 2=0 $
$ \qquad \Rightarrow r=-2+3s $
Setze $r$ in $E_1$ ein und fasse zusammen, um die ie Schnittgerade zu erhalten:
$\qquad$ $ \textcolor{black}{ E_1: \vec{x}= \begin{pmatrix}1\\-1\\3 \end{pmatrix} + (-2+3s)\cdot \begin{pmatrix}1\\-1\\-1 \end{pmatrix} + s\cdot \begin{pmatrix}-1\\2\\-1 \end{pmatrix}} $
$\qquad$ $ \textcolor{black}{ g: \vec{x}= \begin{pmatrix}1\\-1\\3 \end{pmatrix} – 2\cdot \begin{pmatrix}1\\-1\\-1 \end{pmatrix} + 3s\cdot \begin{pmatrix}1\\-1\\-1 \end{pmatrix} + s\cdot \begin{pmatrix}-1\\2\\-1 \end{pmatrix}} $
$ \qquad \textcolor{black}{ g: \vec{x}= \begin{pmatrix}-1\\1\\5 \end{pmatrix} + s\cdot \begin{pmatrix}2\\-1\\-4 \end{pmatrix}} $
$ \qquad \textcolor{black}{ \iff g: \vec{x}= \begin{pmatrix}-1\\1\\5 \end{pmatrix} + s\cdot \begin{pmatrix}2\\-1\\-4 \end{pmatrix}} $
Die Schnittgerade lautet:
$ \qquad\qquad\qquad\qquad\qquad \textcolor{black}{ \iff g: \vec{x}= \begin{pmatrix}-1\\1\\5 \end{pmatrix} + s\cdot \begin{pmatrix}2\\-1\\-4 \end{pmatrix}} $
Graphische Darstellung
$\textcolor{dodgerblue}{E_1} \cap \textcolor{magenta}{E_2}=$
Lagebeziehung zwischen zwei Geraden
Lagebeziehung zwischen zwei Geraden
Zwei Geraden können in der Ebene, im Raum oder auch in höheren Dimensionen unterschiedlich räumlich zueinander ausgerichtet sein.
Mögliche Lage zweier Geraden zueinander
| Geraden identisch | Alle Punkte auf einer Geraden sind auch Punkte auf der anderen Geraden. |
|---|---|
| Geraden schnittpunkt | Zwei Geraden haben einen Schnittpunkt, wenn sie genau einen gemeinsamen Punkt haben. Der Sonderfall, der hier auftreten kann, besteht darin, dass sie im rechten Winkel zueinander stehen. |
| Geraden echt parallel | Zwei Geraden sind echt parallel, wenn sie durch eine Verschiebung identisch werden. |
| Geraden windschief | Zwei Geraden, die sich überhaupt nicht berühren und nicht parallel zueinander sind, sind windschief zueinander. Dies ist nur für Geraden möglich, die im dreidimensionalen Raum oder einem Raum mit höheren Dimensionen liegen. |
Orientierung bestimmen (analytische Geometrie)
Richtungsvektoren von zwei Geraden $\vec{u}$ und $\vec{v}$ sind:
linear abhängig
Wenn die beiden Geraden entweder identisch oder echt parallel sein:
Mathematische Bedeutung:
$\qquad$ für ein $\lambda \in \mathbb{R}$ es gilt: $\qquad \vec{u}= \lambda \cdot \vec{v}$.
Prüfung: Der Ortsvektor der einen Gerade in die andere Geradengleichung einsetzen.
- wenn die Ortsvektoren gleich sind, sind sie identisch
- wenn die Ortsvektoren nicht gleich sind, sind sie parallel.
linear unabhängig
Wenn die beiden Geraden einen Schnittpunkt besitzen, falls nicht, sind sie windschief zueinander.
Prüfung: Die Gleichungen der beiden Geraden gleichsetzen, erhält man eine Lösung, gibt es einen Schnittpunkt, wenn nicht, sind Geraden windschief zueinander.
Übungsaufgaben
Bestimme die Lage der Geraden zueinander und berechne ihren Schnittpunkt wenn er existiert.
-
$\:\:\:
\textcolor{black}{
g: \vec{x}= \begin{pmatrix}3\\7\\3 \end{pmatrix} + r\cdot \begin{pmatrix}6\\9\\-12 \end{pmatrix}}$
$\qquad$
$\qquad$
$
\textcolor{black}{
h: \vec{x}= \begin{pmatrix}9\\14\\4 \end{pmatrix} + s\cdot \begin{pmatrix}-8\\-12\\16 \end{pmatrix}}$
Lösung
Lineare Unabhängigkeit
$\qquad \textcolor{black}{ g: \vec{x}= \begin{pmatrix}3\\7\\3 \end{pmatrix} + r\cdot \begin{pmatrix}6\\9\\-12 \end{pmatrix}}$ $\qquad $ $ \textcolor{black}{ h: \vec{x}= \begin{pmatrix}9\\14\\4 \end{pmatrix} + s\cdot \begin{pmatrix}-8\\-12\\16 \end{pmatrix}}$
Prüfe, ob die Richtungsvektoren linear abhängig sind.
$ \qquad \qquad \qquad \begin{pmatrix}6\\9\\-12 \end{pmatrix} = \lambda \cdot \begin{pmatrix}-8\\-12\\16 \end{pmatrix} $
Stelle ein lineares Gleichungssystem auf und berechne für jedes $\lambda$.
$ \qquad \qquad \qquad \begin{cases} 6=-8\cdot \lambda \:\: &\rightarrow \:\: \lambda=-\frac{3}{4}\\ 9=-12\cdot \lambda \:\: &\rightarrow \:\: \lambda=-\frac{3}{4}\\ -12=16\cdot \lambda \:\: &\rightarrow \:\: \lambda=-\frac{3}{4} \end{cases} $
Mit alle $\lambda$ gleich den selben Wert, sind die Vektoren linear abhängig.
$\qquad$ ➩ Die Vektoren $g$ und $h$ sind linear abhängig.
$\qquad$ ➪ Daher sind die beiden Geraden parallel oder identisch.
Setze den Ortsvektor $\begin{pmatrix}3\\7\\3\end{pmatrix}$ des Aufpunktes von $g$ in die Gleichung der zweiten Gerade $h$ ein.
$ \qquad\qquad \begin{pmatrix}3\\7\\3\end{pmatrix} = \begin{pmatrix}9\\14\\4\end{pmatrix} + s\cdot \begin{pmatrix}-8\\-12\\16\end{pmatrix} $
Stelle wieder ein lineares Gleichungssystem auf und berechne für jedes s:
$ \qquad \qquad\: \begin{cases} 3=9-8\cdot s \:\: &\rightarrow \:\: s=\frac{3}{4} &\rightarrow &s=0,75\\ 7=14-12\cdot s \:\: &\rightarrow \:\: s=-\frac{7}{12} &\rightarrow &s\approx0,59\\ 3=4+16\cdot s \:\: &\rightarrow \:\: s=-\frac{1}{16} &\rightarrow &s\approx-0,063 \end{cases} $
s hat drei verschiedene Werte.
Mit schon zwei unterschiedliche Werte für s, ist das Gleichungssystem nicht lösbar!
$\qquad$ ➩ Der Aufpunkt der Gerade g liegt also nicht auf der Geraden h.
$\qquad$ Die beiden Geraden können nur noch parallel sein.
$\qquad$ ➪ h$||$g oder g$||$h
$\qquad \textcolor{black}{ g: \vec{x}= \begin{pmatrix}3\\7\\3 \end{pmatrix} + r\cdot \begin{pmatrix}6\\9\\-12 \end{pmatrix}}$ $\qquad $ $ \textcolor{black}{ h: \vec{x}= \begin{pmatrix}9\\14\\4 \end{pmatrix} + s\cdot \begin{pmatrix}-8\\-12\\16 \end{pmatrix}}$
Prüfe, ob die Richtungsvektoren linear abhängig sind.
$ \qquad \qquad \qquad \begin{pmatrix}6\\9\\-12 \end{pmatrix} = \lambda \cdot \begin{pmatrix}-8\\-12\\16 \end{pmatrix} $
Stelle ein lineares Gleichungssystem auf und berechne für jedes $\lambda$.
$ \qquad \qquad \qquad \begin{cases} 6=-8\cdot \lambda \:\: &\rightarrow \:\: \lambda=-\frac{3}{4}\\ 9=-12\cdot \lambda \:\: &\rightarrow \:\: \lambda=-\frac{3}{4}\\ -12=16\cdot \lambda \:\: &\rightarrow \:\: \lambda=-\frac{3}{4} \end{cases} $
Mit alle $\lambda$ gleich den selben Wert, sind die Vektoren linear abhängig.
$\qquad$ ➩ Die Vektoren $g$ und $h$ sind linear abhängig.
$\qquad$ ➪ Daher sind die beiden Geraden parallel oder identisch.
Setze den Ortsvektor $\begin{pmatrix}3\\7\\3\end{pmatrix}$ des Aufpunktes von $g$ in die Gleichung der zweiten Gerade $h$ ein.
$ \qquad\qquad \begin{pmatrix}3\\7\\3\end{pmatrix} = \begin{pmatrix}9\\14\\4\end{pmatrix} + s\cdot \begin{pmatrix}-8\\-12\\16\end{pmatrix} $
Stelle wieder ein lineares Gleichungssystem auf und berechne für jedes s:
$ \qquad \qquad\: \begin{cases} 3=9-8\cdot s \:\: &\rightarrow \:\: s=\frac{3}{4} &\rightarrow &s=0,75\\ 7=14-12\cdot s \:\: &\rightarrow \:\: s=-\frac{7}{12} &\rightarrow &s\approx0,59\\ 3=4+16\cdot s \:\: &\rightarrow \:\: s=-\frac{1}{16} &\rightarrow &s\approx-0,063 \end{cases} $
s hat drei verschiedene Werte.
Mit schon zwei unterschiedliche Werte für s, ist das Gleichungssystem nicht lösbar!
$\qquad$ ➩ Der Aufpunkt der Gerade g liegt also nicht auf der Geraden h.
$\qquad$ Die beiden Geraden können nur noch parallel sein.
$\qquad$ ➪ h$||$g oder g$||$h
$\:\:\: \textcolor{black}{ g: \vec{x}= \begin{pmatrix}2\\2\\1 \end{pmatrix} + r\cdot \begin{pmatrix}9\\-3\\6 \end{pmatrix}}$ $\qquad$ $\qquad$ $ \textcolor{black}{ h: \vec{x}= \begin{pmatrix}-7\\5\\-5 \end{pmatrix} + s\cdot \begin{pmatrix}-9\\3\\-6 \end{pmatrix}}$
Lösung
$\qquad \textcolor{black}{ g: \vec{x}= \begin{pmatrix}2\\2\\1 \end{pmatrix} + r\cdot \begin{pmatrix}9\\-3\\6 \end{pmatrix}}$ $\qquad $ $ \textcolor{black}{ h: \vec{x}= \begin{pmatrix}-7\\5\\-5 \end{pmatrix} + s\cdot \begin{pmatrix}-9\\3\\-6 \end{pmatrix}}$
$ \qquad \qquad \qquad \begin{pmatrix}9\\-3\\6 \end{pmatrix} = \lambda \cdot \begin{pmatrix}-9\\3\\-6 \end{pmatrix} $
$\lambda$.
$ \qquad \qquad \qquad \begin{cases} 9=-9\cdot \lambda \:\: &\rightarrow \:\: \lambda=-1\\ -3=3\cdot \lambda \:\: &\rightarrow \:\: \lambda=-1\\ 6=-6\cdot \lambda \:\: &\rightarrow \:\: \lambda=-1 \end{cases} $
$\lambda$
$\qquad$ ➩
$\qquad$ ➪
$\begin{pmatrix}2\\2\\1\end{pmatrix}$
$ \qquad\qquad \begin{pmatrix}2\\2\\1\end{pmatrix} = \begin{pmatrix}-7\\5\\-5\end{pmatrix} + s\cdot \begin{pmatrix}-9\\3\\-6\end{pmatrix} $
$ \qquad \qquad\: \begin{cases} 2=-7-9\cdot s \:\: &s=-1\\ 2=5+3\cdot s \:\: &s=-1\\ 1=-5-6\cdot s \:\: &s=-1 \end{cases} $
$\qquad$ ➩
$\qquad$ ➪
$\:\:\: \textcolor{black}{ g: \vec{x}= \begin{pmatrix}1\\-2\\1 \end{pmatrix} + r\cdot \begin{pmatrix}-4\\-2\\6 \end{pmatrix}}$ $\qquad$
Lösung
Lineare Unabhängigkeit
$\:\:\: \textcolor{black}{ g: \vec{x}= \begin{pmatrix}1\\-2\\1 \end{pmatrix} + r\cdot \begin{pmatrix}-4\\-2\\6 \end{pmatrix}}$ $\qquad$
und
$\qquad$
$
\textcolor{black}{
h: \vec{x}= \begin{pmatrix}-1\\-2\\2 \end{pmatrix} + s\cdot \begin{pmatrix}-4\\-4\\10 \end{pmatrix}}$
Prüfe, ob die Richtungsvektoren linear abhängig sind.
$ \qquad \qquad \qquad \begin{pmatrix}-4\\-2\\6 \end{pmatrix} = \lambda \cdot \begin{pmatrix}-4\\-4\\10 \end{pmatrix} $
Stelle ein lineares Gleichungssystem auf und berechne für jedes $\lambda$.
$ \qquad \qquad \qquad \begin{cases} -4&=-4\cdot \lambda \:\: &\rightarrow \:\: \lambda=-1\\ -2&=-4\cdot \lambda \:\: &\rightarrow \:\: \lambda= \frac{1}{2}\\ 6&=-6\cdot \lambda \:\: &\rightarrow \:\: \lambda= \frac{3}{5} \end{cases} $
Da alle $\lambda$
unterschiedliche Werte haben sind die Vektoren linear unabhängig.
➪
Die beiden Geraden besitzen einen Schnittpunkt oder sind windschief zueinander.
Stelle ein lineares Gleichungssystem (LGS) auf und berechne. (aus g und h)
.
$ \qquad \begin{cases} 1-4r&=-1-4s \\ -2-2r&=-2-4s \\ 1+6r&=2+10s \end{cases} \qquad \xrightarrow[\text{}]{\text{stelle um}} \qquad \begin{cases} 2&=4r-4s \qquad \:\:\:\:\:\:I\\ 0&=2r-4s \qquad \:\:\:\:\:\:II\\ -1&=-6r+10s \qquad III \end{cases} $
$ \:\: I-II:\: 2=2r \Rightarrow \textcolor{green}{\textbf{r=1}}\: |\: r\: in\: III:\: -1=-6(1)+10s \iff 5=10s \Rightarrow$ $\textcolor{blue}{\textbf{s=0,5}} $
Das LGS ist Lösbar, denn haben die Geraden einen Schnittpunkt.
Jetzt r und s in I, II oder III einsetzen um den Schnittpunk zu haben:
$ \qquad \begin{cases} 1-4 (\textcolor{green}{\textbf{1}}) &= -1 - 4 (\textcolor{blue}{\textbf{0,5}}) \\ -2-2 (\textcolor{green}{\textbf{1}}) &= -2 - 4 (\textcolor{blue}{\textbf{0,5}}) \\ 1+6 (\textcolor{green}{\textbf{1}}) &= 2 + 10 (\textcolor{blue}{\textbf{0,5}}) \end{cases} $ $ \Rightarrow $ $ \begin{cases} \textcolor{green}{\textbf{-3}} &= \textcolor{blue}{\textbf{-3}} &\rightarrow \textbf{W.A.}\\ \textcolor{green}{\textbf{-4}} &= \textcolor{blue}{\textbf{-4}} &\rightarrow \textbf{W.A.}\\ \textcolor{green}{\textbf{7}} &= \textcolor{blue}{\textbf{7}} &\rightarrow \textbf{W.A.} \end{cases} $
Damit ist der Schnittpunkt s mit den Koordinaten:
$ \qquad \qquad\qquad\qquad \qquad \qquad \qquad \qquad \qquad \qquad s=\begin{pmatrix}-3\\-4\\7 \end{pmatrix} $
$\:\:\: \textcolor{black}{ g: \vec{x}= \begin{pmatrix}1\\-2\\1 \end{pmatrix} + r\cdot \begin{pmatrix}-4\\-2\\6 \end{pmatrix}}$ $\qquad$
$ \qquad \qquad \qquad \begin{pmatrix}-4\\-2\\6 \end{pmatrix} = \lambda \cdot \begin{pmatrix}-4\\-4\\10 \end{pmatrix} $
$ \qquad \qquad \qquad \begin{cases} -4&=-4\cdot \lambda \:\: &\rightarrow \:\: \lambda=-1\\ -2&=-4\cdot \lambda \:\: &\rightarrow \:\: \lambda= \frac{1}{2}\\ 6&=-6\cdot \lambda \:\: &\rightarrow \:\: \lambda= \frac{3}{5} \end{cases} $
➪
$ \qquad \begin{cases} 1-4r&=-1-4s \\ -2-2r&=-2-4s \\ 1+6r&=2+10s \end{cases} \qquad \xrightarrow[\text{}]{\text{stelle um}} \qquad \begin{cases} 2&=4r-4s \qquad \:\:\:\:\:\:I\\ 0&=2r-4s \qquad \:\:\:\:\:\:II\\ -1&=-6r+10s \qquad III \end{cases} $
$ \:\: I-II:\: 2=2r \Rightarrow \textcolor{green}{\textbf{r=1}}\: |\: r\: in\: III:\: -1=-6(1)+10s \iff 5=10s \Rightarrow$ $\textcolor{blue}{\textbf{s=0,5}} $
$ \qquad \begin{cases} 1-4 (\textcolor{green}{\textbf{1}}) &= -1 - 4 (\textcolor{blue}{\textbf{0,5}}) \\ -2-2 (\textcolor{green}{\textbf{1}}) &= -2 - 4 (\textcolor{blue}{\textbf{0,5}}) \\ 1+6 (\textcolor{green}{\textbf{1}}) &= 2 + 10 (\textcolor{blue}{\textbf{0,5}}) \end{cases} $ $ \Rightarrow $ $ \begin{cases} \textcolor{green}{\textbf{-3}} &= \textcolor{blue}{\textbf{-3}} &\rightarrow \textbf{W.A.}\\ \textcolor{green}{\textbf{-4}} &= \textcolor{blue}{\textbf{-4}} &\rightarrow \textbf{W.A.}\\ \textcolor{green}{\textbf{7}} &= \textcolor{blue}{\textbf{7}} &\rightarrow \textbf{W.A.} \end{cases} $
$ \qquad \qquad\qquad\qquad \qquad \qquad \qquad \qquad \qquad \qquad s=\begin{pmatrix}-3\\-4\\7 \end{pmatrix} $
$\:\:\: \textcolor{black}{ g: \vec{x}= \begin{pmatrix}0\\8\\-7 \end{pmatrix} + r\cdot \begin{pmatrix}1\\2\\-2 \end{pmatrix}}$ $\qquad$
Lösung
Lineare Unabhängigkeit
$\:\:\: \textcolor{black}{ g: \vec{x}= \begin{pmatrix}0\\8\\-7 \end{pmatrix} + r\cdot \begin{pmatrix}1\\2\\-2 \end{pmatrix}}$ $\qquad$
und
$\qquad$
$
\textcolor{black}{
h: \vec{x}= \begin{pmatrix}-9\\0\\7 \end{pmatrix} + s\cdot \begin{pmatrix}3\\1\\-4 \end{pmatrix}}$
Prüfe, ob die Richtungsvektoren linear abhängig sind.
$ \qquad \qquad \qquad \begin{pmatrix}1\\2\\-2 \end{pmatrix} = \lambda \cdot \begin{pmatrix}3\\1\\-4 \end{pmatrix} $
Stelle ein lineares Gleichungssystem auf und berechne für jedes $\lambda$.
$ \qquad \qquad \qquad \begin{cases} 1&=3\cdot \lambda \:\: &\rightarrow \:\: \lambda=0,3 \\ 2&=1\cdot \lambda \:\: &\rightarrow \:\: \lambda=0,5 \\ -2&=-4\cdot \lambda \:\: &\rightarrow \:\: \lambda=0.25 \end{cases} $
Da alle $\lambda$
unterschiedliche Werte haben sind die Vektoren linear unabhängig.
➪
Die beiden Geraden besitzen einen Schnittpunkt oder sind windschief zueinander.
Stelle ein lineares Gleichungssystem (LGS) auf und berechne. (aus g und h)
.
$ \qquad \begin{cases} 0+1r &=-9+3s \\ 8+2r &=0+1s \\ -7-2r &=7-4s \end{cases} \qquad \xrightarrow[\text{}]{\text{stelle um}} \qquad \begin{cases} 9 &=-1r+3s \qquad I\\ 8 &=-2r+1s \qquad II\\ -14 &=2r-4s \qquad \:\:\:III \end{cases} $
$ \:\: II-III:\: -6=-3s \Rightarrow \textcolor{green}{\textbf{s=2}}\: |\: s\: in\: I:\: 9=-r+3(2) \iff \textcolor{blue}{\textbf{r=-3}} $
Das LGS ist Lösbar, denn haben die Geraden einen Schnittpunkt.
Jetzt r und s in I, II oder III einsetzen um den Schnittpunk zu haben:
$ \qquad \begin{cases} 0+1 (\textcolor{blue}{\textbf{-3}}) &= -9 +3 (\textcolor{green}{\textbf{2}}) \\ 8+2 (\textcolor{blue}{\textbf{-3}}) &= 0 +1 (\textcolor{green}{\textbf{2}}) \\ -7-2 (\textcolor{blue}{\textbf{-3}}) &= 7 - 4 (\textcolor{green}{\textbf{2}}) \end{cases} $ $ \Rightarrow $ $ \begin{cases} \textcolor{blue}{\textbf{-3}} &= \textcolor{green}{\textbf{-3}} &\rightarrow \textbf{W.A.}\\ \textcolor{blue}{\textbf{2}} &= \textcolor{green}{\textbf{2}} &\rightarrow \textbf{W.A.}\\ \textcolor{blue}{\textbf{-1}} &= \textcolor{green}{\textbf{-1}} &\rightarrow \textbf{W.A.} \end{cases} $
Damit ist der Schnittpunkt s mit den Koordinaten:
$ \qquad \qquad\qquad\qquad \qquad \qquad \qquad \qquad \qquad \qquad s=\begin{pmatrix}-3\\2\\-1 \end{pmatrix} $
$\:\:\: \textcolor{black}{ g: \vec{x}= \begin{pmatrix}0\\8\\-7 \end{pmatrix} + r\cdot \begin{pmatrix}1\\2\\-2 \end{pmatrix}}$ $\qquad$
$ \qquad \qquad \qquad \begin{pmatrix}1\\2\\-2 \end{pmatrix} = \lambda \cdot \begin{pmatrix}3\\1\\-4 \end{pmatrix} $
$ \qquad \qquad \qquad \begin{cases} 1&=3\cdot \lambda \:\: &\rightarrow \:\: \lambda=0,3 \\ 2&=1\cdot \lambda \:\: &\rightarrow \:\: \lambda=0,5 \\ -2&=-4\cdot \lambda \:\: &\rightarrow \:\: \lambda=0.25 \end{cases} $
➪
$ \qquad \begin{cases} 0+1r &=-9+3s \\ 8+2r &=0+1s \\ -7-2r &=7-4s \end{cases} \qquad \xrightarrow[\text{}]{\text{stelle um}} \qquad \begin{cases} 9 &=-1r+3s \qquad I\\ 8 &=-2r+1s \qquad II\\ -14 &=2r-4s \qquad \:\:\:III \end{cases} $
$ \:\: II-III:\: -6=-3s \Rightarrow \textcolor{green}{\textbf{s=2}}\: |\: s\: in\: I:\: 9=-r+3(2) \iff \textcolor{blue}{\textbf{r=-3}} $
$ \qquad \begin{cases} 0+1 (\textcolor{blue}{\textbf{-3}}) &= -9 +3 (\textcolor{green}{\textbf{2}}) \\ 8+2 (\textcolor{blue}{\textbf{-3}}) &= 0 +1 (\textcolor{green}{\textbf{2}}) \\ -7-2 (\textcolor{blue}{\textbf{-3}}) &= 7 - 4 (\textcolor{green}{\textbf{2}}) \end{cases} $ $ \Rightarrow $ $ \begin{cases} \textcolor{blue}{\textbf{-3}} &= \textcolor{green}{\textbf{-3}} &\rightarrow \textbf{W.A.}\\ \textcolor{blue}{\textbf{2}} &= \textcolor{green}{\textbf{2}} &\rightarrow \textbf{W.A.}\\ \textcolor{blue}{\textbf{-1}} &= \textcolor{green}{\textbf{-1}} &\rightarrow \textbf{W.A.} \end{cases} $
$ \qquad \qquad\qquad\qquad \qquad \qquad \qquad \qquad \qquad \qquad s=\begin{pmatrix}-3\\2\\-1 \end{pmatrix} $