Kurvendiskussion e-Funktion
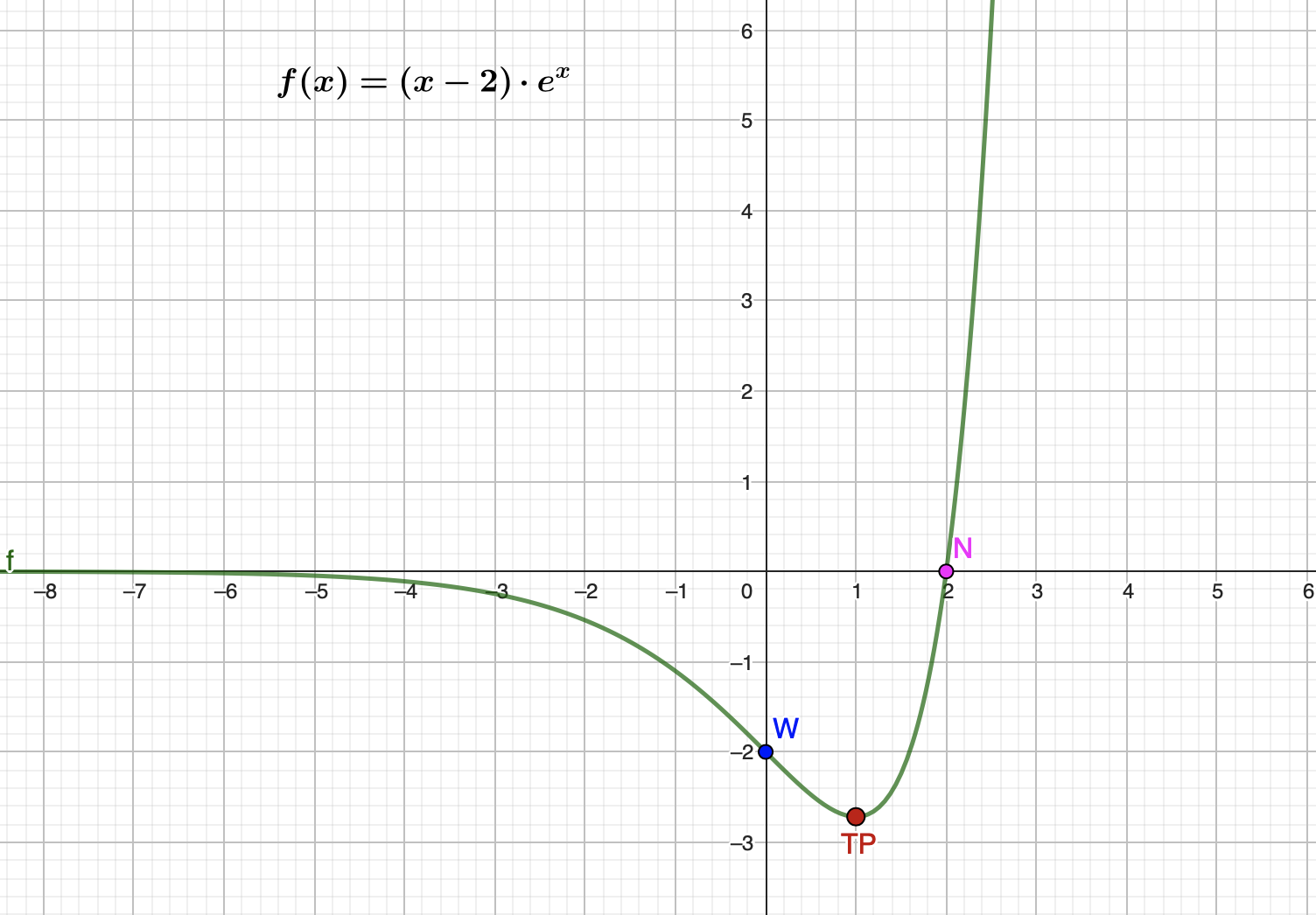
$f(x)=(x-2) \cdot e^{x} $
Lösung
$f(x)=(x-2)
\cdot
e^{x}
$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln\: (Es\: geht\: um\: die\: x-Achse) $
$\qquad$ $ f(-1)=(-1-2) \cdot e^{-1} = -3\cdot e^{-1} =-1,103 $
$\qquad\qquad$ $ \iff $ $\forall x<0$, gibt eine $y$-Werte und die Funktion ist definiert!
$\qquad$ $ f(1)=(1-2) \cdot e^{1} = -1\cdot e^{1} =-e=-2,71 $
$\qquad\qquad$ $ \iff $ $\forall x>0$, gibt eine $y$-Werte und die Funktion ist definiert!
$\qquad$ Die Funktion ist auf beiden Seiten der $x$-Achse definiert.
$\qquad\qquad$ $\Longrightarrow$ $ \textbf {Die Definitionsbereich lautet:} $ $D_{f}=\mathbb{R}=] -\infty; + \infty[$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Nullstellen\: berechnen\: [Ansatz: \: f(x)=0] $
$\qquad$ $ (x-2)\cdot e^{x}=0 \iff \begin{cases} (x-2)=0\:\: \textcolor{red}{|+2}\:\: \longrightarrow x=2\\ oder\\ e^{x}=0,\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ $\Longrightarrow$ $ \textbf { Die Funktion $f$ hat eine Nullstelle bei $x=2$. } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: y-Achsenabschnitt\: berechnen\: [Ansatz: \: y=f(0)] $
$\qquad$ $ y=f(x)=(x-2) \cdot e^{x} $
$\qquad$ $ y=f(0)=(0-2) \cdot e^{0} =-2 \cdot 1=-2 $
$\qquad\qquad$ $\Longrightarrow$ $ \textbf { Die Funktion $f$ schneidet die $y$-Achse in dem Punkt $(0|-2)$. } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Verhalten\: im\: Unendlichen\: bestimmen $
$\qquad$ $ \lim\limits_{x \to -\infty} (x-2)\cdot e^{x} = \lim\limits_{x \to -\infty} e^{x} =0 $ $ \:\:\: | \:\:\: $ $ \lim\limits_{x \to +\infty} (x-2)\cdot e^{x} = \lim\limits_{x \to +\infty} e^{x} =+\infty $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Symmetrieverhalten\: bestimmen $
$\qquad$ Symmetriearten:
$\qquad\qquad$ – Achsensymmetrie zur $y$-Achse: $f(-x)=f(x)$
$\qquad\qquad$ – Punktsymmetrie zur Ursprung: $f(-x)=-f(x)$
$\qquad\qquad$ $ f(-x)=(-x-2) \cdot e^{-x} \neq f(x) \:\: \Longrightarrow $ kein Achsensymmetrie zu $y$-Achse
$\qquad\qquad\qquad\:\:\:\:$ $ = -(x+2) \cdot e^{-x} \neq -f(x) \:\: \Longrightarrow $ kein Punktsymmetrie zum Ursprung
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Extrempunkte\: berechnen $
$\qquad$ Extremstellen berechnen
$\qquad\qquad$ – An Hochpunkte gilt: $f^\prime(x)=0$ und $f^{\prime\prime}(x)<0$
$\qquad\qquad$ – An Tiefpunkte gilt: $\:\:\:f^\prime(x)=0$ und $f^{\prime\prime}(x)>0$
$\qquad$ 1. und 2. Ableitungen (Produktregel)
$\qquad\qquad$ $u(x)=(x-2) \longrightarrow u^\prime(x)=1 \:\:|\:\: v(x)=e^{x} \longrightarrow v^\prime(x)=e^{x}$
$\qquad\qquad$ $\textcolor{red}{* f^\prime(x)=u^\prime(x)\cdot v(x) + u(x)\cdot v^\prime(x)}$
$\qquad\qquad\qquad\:\:\:\:$ $ = 1\cdot e^{x}+(x-2) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = (1+x-2) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = \textcolor{red} { (x-1) \cdot e^{x} } $
$\qquad\qquad$ $t(x)=(x-1) \longrightarrow t^\prime(x)=1 \:\:|\:\: w(x)=e^{x} \longrightarrow w^\prime(x)=e^{x}$
$\qquad\qquad$ $\textcolor{blue}{* f^{\prime\prime}(x)=t^\prime(x)\cdot w(x) + t(x)\cdot w^\prime(x)}$
$\qquad\qquad\qquad\:\:\:\:$ $ = 1\cdot e^{x}+(x-1) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = (1+x-1) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = \textcolor{blue} { x \cdot e^{x} } $
$\qquad$ Nullstelle der ersten Ableitung
$\qquad\qquad$ $ f^\prime(x)=0 $
$\qquad\qquad$ $ (x-1)\cdot e^{x}=0 \iff \begin{cases} (x-1)=0\:\: \textcolor{red}{|+1} \longrightarrow x=1\\ oder\\ e^{x}=0,\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Potentielle Extremstelle bei $x=1$
$\qquad\qquad$ Potentielle Extremstelle in 2. Ableitung einsetzen
$\qquad\qquad\qquad$ $ f^{\prime\prime}(x)= f^{\prime\prime}(1)=1\cdot e^{1} \approx 2,71>0 \iff Tiefpunkt $
$\qquad\qquad$ Extremstellen in ursprüngliche Funktion einsetzen
$\qquad\qquad\qquad$ $f(1)=(1-2)\cdot e^{1}=-e \approx -2,71$
$\qquad$ $ \textbf { Der Tiefpunkt lautet: $T_p(1|-e)$ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Monotonieverhalten\: bestimmen $
$\qquad\qquad$
– Im Intervall von $]-\infty;1[$, fällt der Graph von $f(x)$ streng monoton.
$\qquad\qquad$ – Im Intervall von $]1;+\infty[$, steigt der Graph von $f(x)$ streng monoton.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkt\: und\: Wendetangente\: berechnen\: [Ansatz:\: f^{\prime\prime}(x)=0\: und\: f^{\prime\prime\prime}(x)\neq0] $
$\qquad\qquad$ 3. Abteilung (Produktregel)
$\qquad\qquad\qquad$ $y(x)=x \longrightarrow y^\prime(x)=1\:\: | \:\: z(x)=e^{x} \longrightarrow z^\prime(x)=e^{x}$
$\qquad\qquad\qquad$ $\textcolor{green}{* f^{\prime\prime\prime}(x)=y^\prime(x)\cdot z(x) + y(x)\cdot z^\prime(x)}$
$\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ = 1\cdot e^{x}+x\cdot e^{x} $
$\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ = \textcolor{green}{(1+x)\cdot e^{x}} $
$\qquad\qquad$ Nullstelle der zweite Ableitung
$\qquad\qquad\qquad$ $f^{\prime\prime}(x)=0$
$\qquad\qquad\qquad$ $x\cdot e^{x}=0 \iff \begin{cases} x=0\\ oder\\ e^{x}=0,\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad\qquad$ Potentielle Wendestelle in 3. Ableitung einsetzen
$\qquad\qquad\qquad\qquad$ $f^{\prime\prime\prime}(x)=f^{\prime\prime\prime}(0)=(1+0)\cdot e^{0}=1\neq0$
$\qquad\qquad\qquad\qquad$ $\iff Wendepunkt$ an der Stelle $x=0$
$\qquad\qquad\qquad$ Wendestelle in ursprüngliche Funktion einsetzen
$\qquad\qquad\qquad\qquad$ $f(0)=(0-2)\cdot e^{0}=-2$
$\qquad$ $ \textbf{ Der Wendepunkt lautet:}\: W_p(0|-2) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: Finden $
$\qquad$ Gleichung der Wendetangente:
$\qquad\:\:$ $t_w:\: f(x_0)=f^\prime(x_0)\cdot (x-x_0)+f(x_0)$ mit $ \begin{cases} x_0=0\\ f^\prime(x_0)=m=f^\prime(0)=(0-1)\cdot e^{0}=-1\\ f(x_0)=-2 \end{cases} $
$\qquad\qquad$ $ \Longrightarrow t_w=-1(x-0)+(-2)= -x-2 $
$\qquad$ $ \textbf{ Die Wendetangente lautet: $t_w=-x-2$ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Krümmungen\: ermitteln $
$\qquad$ Linkskrümmung [Links vom Wendepunkt (x=0)]
$\qquad\qquad$ Nimm zum Beispiel die Stelle $x=+1$
$\qquad\qquad$ $f^{\prime\prime}(+1)=+1\cdot e^{+1}=e\approx2,71>0 \longrightarrow linksgekrümmt$
$\qquad$ Rechtskrümmung [Rechts vom Wendepunkt (x=0)]
$\qquad\qquad$ Nimm zum Beispiel die Stelle $x=-1$
$\qquad\qquad$ $f^{\prime\prime}(-1)=-1\cdot e^{-1}=e\approx-0,37<0 \longrightarrow rechtsgekrümmt$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 11.\: Wertebereich\: bestimmen $
$\qquad$ Mit einem Tiefpunkt bei $(1|-e)$ und den Grenzwert $+\infty$,
$\qquad$ Lautet den Wertebereich: $\mathbb{W}=[-e;+\infty[$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 12.\: Funktionsgraph\: zeichnen $
$\qquad$ Wertetabelle erstellen
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln\: (Es\: geht\: um\: die\: x-Achse) $
$\qquad$ $ f(-1)=(-1-2) \cdot e^{-1} = -3\cdot e^{-1} =-1,103 $
$\qquad\qquad$ $ \iff $ $\forall x<0$, gibt eine $y$-Werte und die Funktion ist definiert!
$\qquad$ $ f(1)=(1-2) \cdot e^{1} = -1\cdot e^{1} =-e=-2,71 $
$\qquad\qquad$ $ \iff $ $\forall x>0$, gibt eine $y$-Werte und die Funktion ist definiert!
$\qquad$ Die Funktion ist auf beiden Seiten der $x$-Achse definiert.
$\qquad\qquad$ $\Longrightarrow$ $ \textbf {Die Definitionsbereich lautet:} $ $D_{f}=\mathbb{R}=] -\infty; + \infty[$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Nullstellen\: berechnen\: [Ansatz: \: f(x)=0] $
$\qquad$ $ (x-2)\cdot e^{x}=0 \iff \begin{cases} (x-2)=0\:\: \textcolor{red}{|+2}\:\: \longrightarrow x=2\\ oder\\ e^{x}=0,\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ $\Longrightarrow$ $ \textbf { Die Funktion $f$ hat eine Nullstelle bei $x=2$. } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: y-Achsenabschnitt\: berechnen\: [Ansatz: \: y=f(0)] $
$\qquad$ $ y=f(x)=(x-2) \cdot e^{x} $
$\qquad$ $ y=f(0)=(0-2) \cdot e^{0} =-2 \cdot 1=-2 $
$\qquad\qquad$ $\Longrightarrow$ $ \textbf { Die Funktion $f$ schneidet die $y$-Achse in dem Punkt $(0|-2)$. } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Verhalten\: im\: Unendlichen\: bestimmen $
$\qquad$ $ \lim\limits_{x \to -\infty} (x-2)\cdot e^{x} = \lim\limits_{x \to -\infty} e^{x} =0 $ $ \:\:\: | \:\:\: $ $ \lim\limits_{x \to +\infty} (x-2)\cdot e^{x} = \lim\limits_{x \to +\infty} e^{x} =+\infty $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Symmetrieverhalten\: bestimmen $
$\qquad$ Symmetriearten:
$\qquad\qquad$ – Achsensymmetrie zur $y$-Achse: $f(-x)=f(x)$
$\qquad\qquad$ – Punktsymmetrie zur Ursprung: $f(-x)=-f(x)$
$\qquad\qquad$ $ f(-x)=(-x-2) \cdot e^{-x} \neq f(x) \:\: \Longrightarrow $ kein Achsensymmetrie zu $y$-Achse
$\qquad\qquad\qquad\:\:\:\:$ $ = -(x+2) \cdot e^{-x} \neq -f(x) \:\: \Longrightarrow $ kein Punktsymmetrie zum Ursprung
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Extrempunkte\: berechnen $
$\qquad$ Extremstellen berechnen
$\qquad\qquad$ – An Hochpunkte gilt: $f^\prime(x)=0$ und $f^{\prime\prime}(x)<0$
$\qquad\qquad$ – An Tiefpunkte gilt: $\:\:\:f^\prime(x)=0$ und $f^{\prime\prime}(x)>0$
$\qquad$ 1. und 2. Ableitungen (Produktregel)
$\qquad\qquad$ $u(x)=(x-2) \longrightarrow u^\prime(x)=1 \:\:|\:\: v(x)=e^{x} \longrightarrow v^\prime(x)=e^{x}$
$\qquad\qquad$ $\textcolor{red}{* f^\prime(x)=u^\prime(x)\cdot v(x) + u(x)\cdot v^\prime(x)}$
$\qquad\qquad\qquad\:\:\:\:$ $ = 1\cdot e^{x}+(x-2) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = (1+x-2) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = \textcolor{red} { (x-1) \cdot e^{x} } $
$\qquad\qquad$ $t(x)=(x-1) \longrightarrow t^\prime(x)=1 \:\:|\:\: w(x)=e^{x} \longrightarrow w^\prime(x)=e^{x}$
$\qquad\qquad$ $\textcolor{blue}{* f^{\prime\prime}(x)=t^\prime(x)\cdot w(x) + t(x)\cdot w^\prime(x)}$
$\qquad\qquad\qquad\:\:\:\:$ $ = 1\cdot e^{x}+(x-1) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = (1+x-1) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = \textcolor{blue} { x \cdot e^{x} } $
$\qquad$ Nullstelle der ersten Ableitung
$\qquad\qquad$ $ f^\prime(x)=0 $
$\qquad\qquad$ $ (x-1)\cdot e^{x}=0 \iff \begin{cases} (x-1)=0\:\: \textcolor{red}{|+1} \longrightarrow x=1\\ oder\\ e^{x}=0,\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Potentielle Extremstelle bei $x=1$
$\qquad\qquad$ Potentielle Extremstelle in 2. Ableitung einsetzen
$\qquad\qquad\qquad$ $ f^{\prime\prime}(x)= f^{\prime\prime}(1)=1\cdot e^{1} \approx 2,71>0 \iff Tiefpunkt $
$\qquad\qquad$ Extremstellen in ursprüngliche Funktion einsetzen
$\qquad\qquad\qquad$ $f(1)=(1-2)\cdot e^{1}=-e \approx -2,71$
$\qquad$ $ \textbf { Der Tiefpunkt lautet: $T_p(1|-e)$ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Monotonieverhalten\: bestimmen $
| Funktion | $-\infty$ | 1 | $+\infty$ |
| $f^\prime(x)$ | $-$ | $\vert$ | $+$ |
| $f(x)$ | $\searrow$ | $-e$ | $\nearrow$ |
$\qquad\qquad$ – Im Intervall von $]1;+\infty[$, steigt der Graph von $f(x)$ streng monoton.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkt\: und\: Wendetangente\: berechnen\: [Ansatz:\: f^{\prime\prime}(x)=0\: und\: f^{\prime\prime\prime}(x)\neq0] $
$\qquad\qquad$ 3. Abteilung (Produktregel)
$\qquad\qquad\qquad$ $y(x)=x \longrightarrow y^\prime(x)=1\:\: | \:\: z(x)=e^{x} \longrightarrow z^\prime(x)=e^{x}$
$\qquad\qquad\qquad$ $\textcolor{green}{* f^{\prime\prime\prime}(x)=y^\prime(x)\cdot z(x) + y(x)\cdot z^\prime(x)}$
$\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ = 1\cdot e^{x}+x\cdot e^{x} $
$\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ = \textcolor{green}{(1+x)\cdot e^{x}} $
$\qquad\qquad$ Nullstelle der zweite Ableitung
$\qquad\qquad\qquad$ $f^{\prime\prime}(x)=0$
$\qquad\qquad\qquad$ $x\cdot e^{x}=0 \iff \begin{cases} x=0\\ oder\\ e^{x}=0,\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad\qquad$ Potentielle Wendestelle in 3. Ableitung einsetzen
$\qquad\qquad\qquad\qquad$ $f^{\prime\prime\prime}(x)=f^{\prime\prime\prime}(0)=(1+0)\cdot e^{0}=1\neq0$
$\qquad\qquad\qquad\qquad$ $\iff Wendepunkt$ an der Stelle $x=0$
$\qquad\qquad\qquad$ Wendestelle in ursprüngliche Funktion einsetzen
$\qquad\qquad\qquad\qquad$ $f(0)=(0-2)\cdot e^{0}=-2$
$\qquad$ $ \textbf{ Der Wendepunkt lautet:}\: W_p(0|-2) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: Finden $
$\qquad$ Gleichung der Wendetangente:
$\qquad\:\:$ $t_w:\: f(x_0)=f^\prime(x_0)\cdot (x-x_0)+f(x_0)$ mit $ \begin{cases} x_0=0\\ f^\prime(x_0)=m=f^\prime(0)=(0-1)\cdot e^{0}=-1\\ f(x_0)=-2 \end{cases} $
$\qquad\qquad$ $ \Longrightarrow t_w=-1(x-0)+(-2)= -x-2 $
$\qquad$ $ \textbf{ Die Wendetangente lautet: $t_w=-x-2$ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Krümmungen\: ermitteln $
$\qquad$ Linkskrümmung [Links vom Wendepunkt (x=0)]
$\qquad\qquad$ Nimm zum Beispiel die Stelle $x=+1$
$\qquad\qquad$ $f^{\prime\prime}(+1)=+1\cdot e^{+1}=e\approx2,71>0 \longrightarrow linksgekrümmt$
$\qquad$ Rechtskrümmung [Rechts vom Wendepunkt (x=0)]
$\qquad\qquad$ Nimm zum Beispiel die Stelle $x=-1$
$\qquad\qquad$ $f^{\prime\prime}(-1)=-1\cdot e^{-1}=e\approx-0,37<0 \longrightarrow rechtsgekrümmt$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 11.\: Wertebereich\: bestimmen $
$\qquad$ Mit einem Tiefpunkt bei $(1|-e)$ und den Grenzwert $+\infty$,
$\qquad$ Lautet den Wertebereich: $\mathbb{W}=[-e;+\infty[$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 12.\: Funktionsgraph\: zeichnen $
$\qquad$ Wertetabelle erstellen
| x | -2,5 | -2 | -1 | 1 | 1,5 | 2,5 | 3 |
| f(x) | -0,3 | -0,5 | -1,1 | -2,7 | -2,2 | 6,1 | 20,1 |

$f(x)= \frac{1}{4}e^{2x} \cdot (x^2-2) $
Lösung
$f(x)=
\frac{1}{4}e^{2x} \cdot (x^2-2)
$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln\: (Es\: geht\: um\: die\: x-Achse) $
$\qquad\:\:$ $ \begin{cases} \frac{1}{4}e^{2x} \in\mathbb{R}\\ \\ (x^2-2) \in\mathbb{R} \end{cases} \Longrightarrow \:\: D_f=\mathbb{R}=]-\infty;+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln\: (Es\: geht\: um\: die\: y-Achse) $
$\qquad\:\:$ $ \forall y \in \mathbb{R}, y> -\frac{1}{4}e^{2x}\\ \:\: \Longrightarrow \:\: W_f=]-\frac{1}{4}e^{2x};+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $f(x)=\frac{1}{4}e^{2x} \cdot(x^2-2)\:\: mit \:\: \begin{cases} u(x)=\frac{1}{4}e^{2x} \:\: \longrightarrow u^\prime(x)=\frac{1}{2}e^{2x}\\ \\ v(x)=(x^2-2) \:\: \longrightarrow v^\prime(x)=2x \end{cases} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x) \cdot v(x)+u(x) \cdot v^\prime(x) = \frac{1}{2}e^{2x} \cdot (x^2-2) + \frac{1}{4}e^{2x} \cdot 2x $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:$ $ = \underline{e^{2x} \cdot (\frac{1}{2}x^{2} + \frac{1}{2}x-1)} $
$\qquad\:\:$ Zweite Ableitung: Mit Produktregel
$\qquad\qquad$ $f^{\prime\prime}(x)= \underline{e^{2x} \cdot (x^2+2x- \frac{3}{2})} $
$\qquad\:\:$ Dritte Ableitung: Mit Produktregel
$\qquad\qquad$ $f^{\prime\prime\prime}(x)= \underline{e^{2x} \cdot (2x^2+6x-1)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)= \frac{1}{4}e^{2\cdot 0} \cdot (0^2-2)= -\frac{1}{2} \longrightarrow S_y(0|- \frac{1}{2}) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\:(Schnittpunkt\: mit\: der\: x-Achse\: \longrightarrow \: y=f(x)=0) $
$\qquad\:\:$ $ f(x)=0 \iff \frac{1}{4}e^{2x} \cdot (x^2-2)=0 \iff \begin{cases} \frac{1}{4}e^{2x}=0\:\: \textcolor{red}{n.L.}\\ \\ (x^2-2)=0\:\: \textcolor{red}{|+2} \longrightarrow x^2=2\:\: \textcolor{red}{| \sqrt{…}} \end{cases} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ \longrightarrow x_{1/2}= \pm \sqrt{2} $
$\qquad\:\:$ Die Nullstellen sind: $N_1(\sqrt{2}|0)$ und $N_2(-\sqrt{2}|0)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)= \frac{1}{4}e^{2(-x)} \cdot [(-x)^2-2]= \frac{1}{4}e^{-2x} \cdot (x^2-2) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ \neq f(x) \longrightarrow keine\: Achsensymmetrie $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ \neq -f(x) \longrightarrow keine\: Punktsymmetrie $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^\prime(x)=0, f^{\prime\prime}(x) \neq0$
$\qquad\:\:$ $ f^\prime(x)=0 \iff e^{2x} \cdot (\frac{1}{2}x^2+\frac{1}{2}x-1)=0 \iff \begin{cases} e^{2x}=0\:\: \textcolor{red}{n.L.}\\ oder\\ \frac{1}{2}x^2+\frac{1}{2}x-1=0 \end{cases} $
$\qquad\:\:$ $ \frac{1}{2}x^2+\frac{1}{2}x-1=0\:\: \textcolor{red}{|\cdot2} $
$\qquad\qquad$ $ x^2+x-2=0\:\: (Löse\: mit\: p-q-Formel)\:\:\:\: |\:\:\:\: x_1=1\:\: und\:\: x_2=-2 $
$\qquad\:\:$ Es gibt Extrempunkte an der Stelle $x_1=1$ und $x_2=-2$
$\qquad\:\:$ $ f^{\prime\prime}(1)= e^{2(1)} \cdot [1^2+2(1)- \frac{3}{2}]=11,08>0 \longrightarrow Tiefpunkt $
$\qquad\:\:$ $ f^{\prime\prime}(-2)= e^{2(-2)} \cdot [(-2)^2+2(-2)- \frac{3}{2}]=-0,027<0 \longrightarrow Hochpunkt $
$\qquad\qquad$ $ TP[(1)|f(1)]= (1|-\frac{1}{4}e^2)\:\: \:\:und\:\:\:\: HP[(-2)|f(-2)]= (-2|\frac{1}{2e^4}) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0, f^{\prime\prime\prime}(x) \neq0$
$\qquad\:\:$ $ f^{\prime\prime}(x)=0 \iff e^{2x} \cdot (x^2+2x-\frac{3}{2})=0 \iff \begin{cases} e^{2x}=0\:\: \textcolor{red}{n.L.}\\ oder\\ x^2+2x-\frac{3}{2}=0 \end{cases} $
$\qquad\:\:$ $ x^2+2x-\frac{3}{2}=0\:\: (Löse\: mit\: p-q-Formel)\:\:\:\: |\:\:\:\: x_1=0,58\:\: und\:\: x_2=-2,58 $
$\qquad\:\:$ Es gibt Wendepunkte an der Stelle $x_1=0,58$ und $x_2=–2,58$
$\qquad\:\:$ $ f^{\prime\prime\prime}(0,58)=10,05>0 \longrightarrow RL-gekrümmt $
$\qquad\:\:$ $ f^{\prime\prime\prime}(-2,58)=-0,018<0 \longrightarrow LR-gekrümmt $
$\qquad\:\:$ $ W_1[(0,58)|f(0,58)]= (0,58|-1,33) $ und $ W_2[(-2,58)|f(-2,58)]= (-2,58|0,007) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w_1}: f(x_{w_1})=f^\prime(x_{w_1}) \cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=0,58\\ \\ f^\prime(x_{w_1})=-1,72 \\ \\ f(x_{w_1})=-1,33 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_1}}=-1,72(x-0,58)+(-1,33)= \underline{-1,72x-0,33} $
$\qquad\qquad$ $ t_{w_2}: f(x_{w_2})=f^\prime(x_{w_2}) \cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=-2,58\\ \\ f^\prime(x_{w_2})=0,006 \\ \\ f(x_{w_2})=0,007 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_2}}=0,006(x+2,58)+0,007= \underline{0,006x+0,02} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=0 \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)= +\infty $
$\qquad\:\:$ $ \textbf{Schaubild:} $

$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln\: (Es\: geht\: um\: die\: x-Achse) $
$\qquad\:\:$ $ \begin{cases} \frac{1}{4}e^{2x} \in\mathbb{R}\\ \\ (x^2-2) \in\mathbb{R} \end{cases} \Longrightarrow \:\: D_f=\mathbb{R}=]-\infty;+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln\: (Es\: geht\: um\: die\: y-Achse) $
$\qquad\:\:$ $ \forall y \in \mathbb{R}, y> -\frac{1}{4}e^{2x}\\ \:\: \Longrightarrow \:\: W_f=]-\frac{1}{4}e^{2x};+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $f(x)=\frac{1}{4}e^{2x} \cdot(x^2-2)\:\: mit \:\: \begin{cases} u(x)=\frac{1}{4}e^{2x} \:\: \longrightarrow u^\prime(x)=\frac{1}{2}e^{2x}\\ \\ v(x)=(x^2-2) \:\: \longrightarrow v^\prime(x)=2x \end{cases} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x) \cdot v(x)+u(x) \cdot v^\prime(x) = \frac{1}{2}e^{2x} \cdot (x^2-2) + \frac{1}{4}e^{2x} \cdot 2x $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:$ $ = \underline{e^{2x} \cdot (\frac{1}{2}x^{2} + \frac{1}{2}x-1)} $
$\qquad\:\:$ Zweite Ableitung: Mit Produktregel
$\qquad\qquad$ $f^{\prime\prime}(x)= \underline{e^{2x} \cdot (x^2+2x- \frac{3}{2})} $
$\qquad\:\:$ Dritte Ableitung: Mit Produktregel
$\qquad\qquad$ $f^{\prime\prime\prime}(x)= \underline{e^{2x} \cdot (2x^2+6x-1)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)= \frac{1}{4}e^{2\cdot 0} \cdot (0^2-2)= -\frac{1}{2} \longrightarrow S_y(0|- \frac{1}{2}) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\:(Schnittpunkt\: mit\: der\: x-Achse\: \longrightarrow \: y=f(x)=0) $
$\qquad\:\:$ $ f(x)=0 \iff \frac{1}{4}e^{2x} \cdot (x^2-2)=0 \iff \begin{cases} \frac{1}{4}e^{2x}=0\:\: \textcolor{red}{n.L.}\\ \\ (x^2-2)=0\:\: \textcolor{red}{|+2} \longrightarrow x^2=2\:\: \textcolor{red}{| \sqrt{…}} \end{cases} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ \longrightarrow x_{1/2}= \pm \sqrt{2} $
$\qquad\:\:$ Die Nullstellen sind: $N_1(\sqrt{2}|0)$ und $N_2(-\sqrt{2}|0)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)= \frac{1}{4}e^{2(-x)} \cdot [(-x)^2-2]= \frac{1}{4}e^{-2x} \cdot (x^2-2) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ \neq f(x) \longrightarrow keine\: Achsensymmetrie $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ \neq -f(x) \longrightarrow keine\: Punktsymmetrie $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^\prime(x)=0, f^{\prime\prime}(x) \neq0$
$\qquad\:\:$ $ f^\prime(x)=0 \iff e^{2x} \cdot (\frac{1}{2}x^2+\frac{1}{2}x-1)=0 \iff \begin{cases} e^{2x}=0\:\: \textcolor{red}{n.L.}\\ oder\\ \frac{1}{2}x^2+\frac{1}{2}x-1=0 \end{cases} $
$\qquad\:\:$ $ \frac{1}{2}x^2+\frac{1}{2}x-1=0\:\: \textcolor{red}{|\cdot2} $
$\qquad\qquad$ $ x^2+x-2=0\:\: (Löse\: mit\: p-q-Formel)\:\:\:\: |\:\:\:\: x_1=1\:\: und\:\: x_2=-2 $
$\qquad\:\:$ Es gibt Extrempunkte an der Stelle $x_1=1$ und $x_2=-2$
$\qquad\:\:$ $ f^{\prime\prime}(1)= e^{2(1)} \cdot [1^2+2(1)- \frac{3}{2}]=11,08>0 \longrightarrow Tiefpunkt $
$\qquad\:\:$ $ f^{\prime\prime}(-2)= e^{2(-2)} \cdot [(-2)^2+2(-2)- \frac{3}{2}]=-0,027<0 \longrightarrow Hochpunkt $
$\qquad\qquad$ $ TP[(1)|f(1)]= (1|-\frac{1}{4}e^2)\:\: \:\:und\:\:\:\: HP[(-2)|f(-2)]= (-2|\frac{1}{2e^4}) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0, f^{\prime\prime\prime}(x) \neq0$
$\qquad\:\:$ $ f^{\prime\prime}(x)=0 \iff e^{2x} \cdot (x^2+2x-\frac{3}{2})=0 \iff \begin{cases} e^{2x}=0\:\: \textcolor{red}{n.L.}\\ oder\\ x^2+2x-\frac{3}{2}=0 \end{cases} $
$\qquad\:\:$ $ x^2+2x-\frac{3}{2}=0\:\: (Löse\: mit\: p-q-Formel)\:\:\:\: |\:\:\:\: x_1=0,58\:\: und\:\: x_2=-2,58 $
$\qquad\:\:$ Es gibt Wendepunkte an der Stelle $x_1=0,58$ und $x_2=–2,58$
$\qquad\:\:$ $ f^{\prime\prime\prime}(0,58)=10,05>0 \longrightarrow RL-gekrümmt $
$\qquad\:\:$ $ f^{\prime\prime\prime}(-2,58)=-0,018<0 \longrightarrow LR-gekrümmt $
$\qquad\:\:$ $ W_1[(0,58)|f(0,58)]= (0,58|-1,33) $ und $ W_2[(-2,58)|f(-2,58)]= (-2,58|0,007) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w_1}: f(x_{w_1})=f^\prime(x_{w_1}) \cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=0,58\\ \\ f^\prime(x_{w_1})=-1,72 \\ \\ f(x_{w_1})=-1,33 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_1}}=-1,72(x-0,58)+(-1,33)= \underline{-1,72x-0,33} $
$\qquad\qquad$ $ t_{w_2}: f(x_{w_2})=f^\prime(x_{w_2}) \cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=-2,58\\ \\ f^\prime(x_{w_2})=0,006 \\ \\ f(x_{w_2})=0,007 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_2}}=0,006(x+2,58)+0,007= \underline{0,006x+0,02} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=0 \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)= +\infty $
$\qquad\:\:$ $ \textbf{Schaubild:} $

$f(x)=e^{1-x^2}$
Lösung
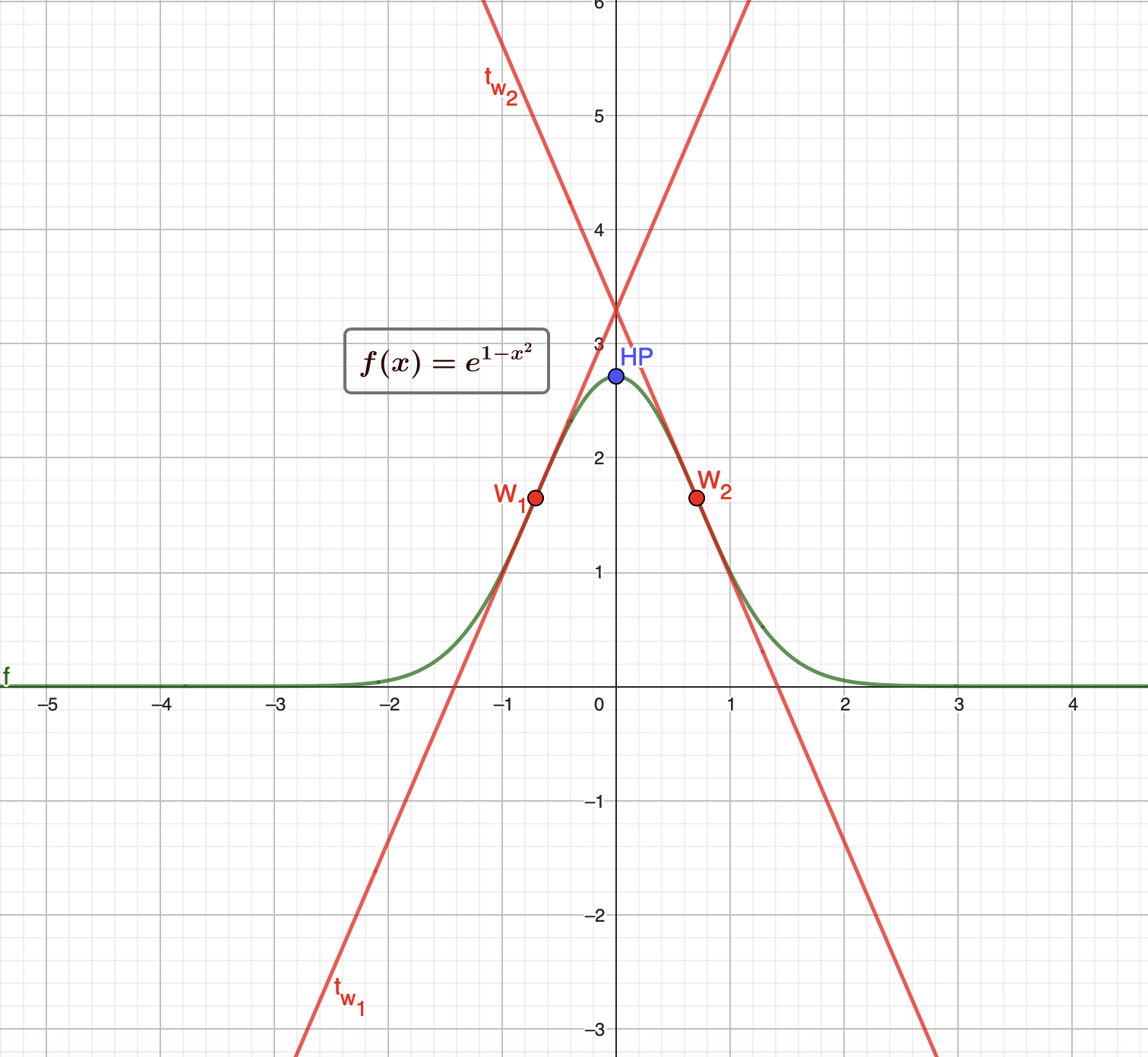
$f(x)=e^{1-x^2}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ D_f=\forall x\in\mathbb{R}, -\infty < x < +\infty \longrightarrow D_f=]-\infty;+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ W_f=\forall y \in\mathbb{R}, 0 < y < e \longrightarrow W_f=]0;e[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $ f(x)=e^{1-x^2} $
$\qquad\qquad$ Mit Kettenregel: $ f^\prime(x)=(1-x^2)^\prime \cdot e^{1-x^2}= \underline{-2x \cdot e^{1-x^2}} $
$\qquad\:\:$ Zweite Ableitung:
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^\prime(x) \cdot v(x)+ u(x) \cdot v^\prime(x)| \begin{cases} u(x)=-2x \longrightarrow u^\prime(x)=-2\\ \\ v(x)=e^{1-x^2} \longrightarrow v^\prime(x)=-2x\cdot e^{1-x^2} \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-2\cdot e^{1-x^2}+ (-2x)\cdot (-2x) \cdot e^{1-x^2}=-2\cdot e^{1-x^2}+ 4x^2\cdot e^{1-x^2} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad$ $ =\underline{(-1+2x^2)\cdot 2e^{1-x^2}} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ Mit Produktregel und Kettenregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=u^\prime(x) \cdot v(x)+ u(x) \cdot v^\prime(x)| \begin{cases} u(x)=-1+2x^2 \longrightarrow u^\prime(x)=4x\\ \\ v(x)=2e^{1-x^2} \longrightarrow v^\prime(x)=-4x\cdot e^{1-x^2} \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=4x\cdot 2e^{1-x^2}+ (-1+2x^2)\cdot (-4x) \cdot e^{1-x^2}=4e^{1-x^2}(2x+1x-2x^3) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ =\underline{4e^{1-x^2}(3x-2x^3)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=e^{1-0^2}=e \longrightarrow \underline{S_y(0|e)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\:Nullstellen\: (Schnittpunkt\: mit\: der\: x-Achse: \longrightarrow y=f(x)=0) $
$\qquad\:\:$ $ f(x)=0 \iff e^{1-x^2}=0\:\: \textcolor{red}{n.L.}\:\: \longrightarrow keine Nullstellen $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\:Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=e^{1-(-x)^2}=e^{1-x^2}=f(x) \longrightarrow Gerade\: Funktion, Achsensymmetrie $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\:Extrempunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^\prime(x)=0, f^{\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^\prime(x)=0 \iff -2x\cdot e^{1-x^2}=0 \iff \begin{cases} -2x=0 \longrightarrow x=0\\ \\ e^{1-x^2}=0\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Es gibt ein Extrempunkt an der Stelle $x=0$
$\qquad\qquad$ $ f^{\prime\prime}(0)=[-1+2(0)^2]\cdot 2e^{1-0^2}=-2e<0 \longrightarrow Hochpunkt $
$\qquad\qquad\qquad\qquad\qquad$ $ \underline{HP[(0)|f(0)]=(0|e)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\:Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0, f^{\prime\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^{\prime\prime}(x)=0 \iff (-1+2x^2)\cdot 2e^{1-x^2}=0 $
$\qquad\qquad$ $ \iff \begin{cases} -1+2x^2=0\: \textcolor{red}{|+1}, 2x^2=1\: \textcolor{red}{|:2}, x^2=\frac{1}{2}\: \textcolor{red}{|\sqrt{…}}\: \longrightarrow \: \begin{cases} x_1=-0,707\\ \\ x_2=+0,707 \end{cases} \\ \\ 2e^{1-x^2}=0\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Es gibt Wendepunkte an der Stelle $x_1=-0,707$ und $x_2=+0,707$
$\qquad\qquad$ $ f^{\prime\prime\prime}(-0,707)=-9,33<0 \longrightarrow LR-gekrümmt $
$\qquad\qquad$ $ f^{\prime\prime\prime}(+0,707)=+9,33>0 \longrightarrow RL-gekrümmt $
$\qquad\qquad$ $ W_1[(-0,707)|f(-0,707)]=\underline{(-0,707|1,65)}\:\: | \:\: W_2[(0,707)|f(0,707)]=\underline{(0,707|1,65)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\:Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w_1}: f(x_{w_1})=f^\prime(x_{w_1})\cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=-0,707\\ \\ f^\prime(x_{w_1})=2,33\\ \\ f(x_{w_1})=1,65 \end{cases} $
$\qquad\qquad\qquad$ $ t_{w_1}=2,33(x+0,707)+1,65=\underline{2,33x+3,3} $
$\qquad\qquad$ $ t_{w_2}: f(x_{w_2})=f^\prime(x_{w_2})\cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=0,707\\ \\ f^\prime(x_{w_2})=-2,33\\ \\ f(x_{w_2})=1,65 \end{cases} $
$\qquad\qquad\qquad$ $ t_{w_2}=-2,33(x-0,707)+1,65=\underline{-2,33x+3,3} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\:Verhalten\:im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=0 \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $
$\qquad\:\:$ Schaubild:
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ D_f=\forall x\in\mathbb{R}, -\infty < x < +\infty \longrightarrow D_f=]-\infty;+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ W_f=\forall y \in\mathbb{R}, 0 < y < e \longrightarrow W_f=]0;e[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $ f(x)=e^{1-x^2} $
$\qquad\qquad$ Mit Kettenregel: $ f^\prime(x)=(1-x^2)^\prime \cdot e^{1-x^2}= \underline{-2x \cdot e^{1-x^2}} $
$\qquad\:\:$ Zweite Ableitung:
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^\prime(x) \cdot v(x)+ u(x) \cdot v^\prime(x)| \begin{cases} u(x)=-2x \longrightarrow u^\prime(x)=-2\\ \\ v(x)=e^{1-x^2} \longrightarrow v^\prime(x)=-2x\cdot e^{1-x^2} \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-2\cdot e^{1-x^2}+ (-2x)\cdot (-2x) \cdot e^{1-x^2}=-2\cdot e^{1-x^2}+ 4x^2\cdot e^{1-x^2} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad$ $ =\underline{(-1+2x^2)\cdot 2e^{1-x^2}} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ Mit Produktregel und Kettenregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=u^\prime(x) \cdot v(x)+ u(x) \cdot v^\prime(x)| \begin{cases} u(x)=-1+2x^2 \longrightarrow u^\prime(x)=4x\\ \\ v(x)=2e^{1-x^2} \longrightarrow v^\prime(x)=-4x\cdot e^{1-x^2} \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=4x\cdot 2e^{1-x^2}+ (-1+2x^2)\cdot (-4x) \cdot e^{1-x^2}=4e^{1-x^2}(2x+1x-2x^3) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ =\underline{4e^{1-x^2}(3x-2x^3)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=e^{1-0^2}=e \longrightarrow \underline{S_y(0|e)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\:Nullstellen\: (Schnittpunkt\: mit\: der\: x-Achse: \longrightarrow y=f(x)=0) $
$\qquad\:\:$ $ f(x)=0 \iff e^{1-x^2}=0\:\: \textcolor{red}{n.L.}\:\: \longrightarrow keine Nullstellen $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\:Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=e^{1-(-x)^2}=e^{1-x^2}=f(x) \longrightarrow Gerade\: Funktion, Achsensymmetrie $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\:Extrempunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^\prime(x)=0, f^{\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^\prime(x)=0 \iff -2x\cdot e^{1-x^2}=0 \iff \begin{cases} -2x=0 \longrightarrow x=0\\ \\ e^{1-x^2}=0\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Es gibt ein Extrempunkt an der Stelle $x=0$
$\qquad\qquad$ $ f^{\prime\prime}(0)=[-1+2(0)^2]\cdot 2e^{1-0^2}=-2e<0 \longrightarrow Hochpunkt $
$\qquad\qquad\qquad\qquad\qquad$ $ \underline{HP[(0)|f(0)]=(0|e)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\:Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0, f^{\prime\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^{\prime\prime}(x)=0 \iff (-1+2x^2)\cdot 2e^{1-x^2}=0 $
$\qquad\qquad$ $ \iff \begin{cases} -1+2x^2=0\: \textcolor{red}{|+1}, 2x^2=1\: \textcolor{red}{|:2}, x^2=\frac{1}{2}\: \textcolor{red}{|\sqrt{…}}\: \longrightarrow \: \begin{cases} x_1=-0,707\\ \\ x_2=+0,707 \end{cases} \\ \\ 2e^{1-x^2}=0\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Es gibt Wendepunkte an der Stelle $x_1=-0,707$ und $x_2=+0,707$
$\qquad\qquad$ $ f^{\prime\prime\prime}(-0,707)=-9,33<0 \longrightarrow LR-gekrümmt $
$\qquad\qquad$ $ f^{\prime\prime\prime}(+0,707)=+9,33>0 \longrightarrow RL-gekrümmt $
$\qquad\qquad$ $ W_1[(-0,707)|f(-0,707)]=\underline{(-0,707|1,65)}\:\: | \:\: W_2[(0,707)|f(0,707)]=\underline{(0,707|1,65)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\:Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w_1}: f(x_{w_1})=f^\prime(x_{w_1})\cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=-0,707\\ \\ f^\prime(x_{w_1})=2,33\\ \\ f(x_{w_1})=1,65 \end{cases} $
$\qquad\qquad\qquad$ $ t_{w_1}=2,33(x+0,707)+1,65=\underline{2,33x+3,3} $
$\qquad\qquad$ $ t_{w_2}: f(x_{w_2})=f^\prime(x_{w_2})\cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=0,707\\ \\ f^\prime(x_{w_2})=-2,33\\ \\ f(x_{w_2})=1,65 \end{cases} $
$\qquad\qquad\qquad$ $ t_{w_2}=-2,33(x-0,707)+1,65=\underline{-2,33x+3,3} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\:Verhalten\:im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=0 \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $
$\qquad\:\:$ Schaubild:

$f(x)=(1-x^2)\cdot e^{- \frac{1}{2}x^2}$
Lösung
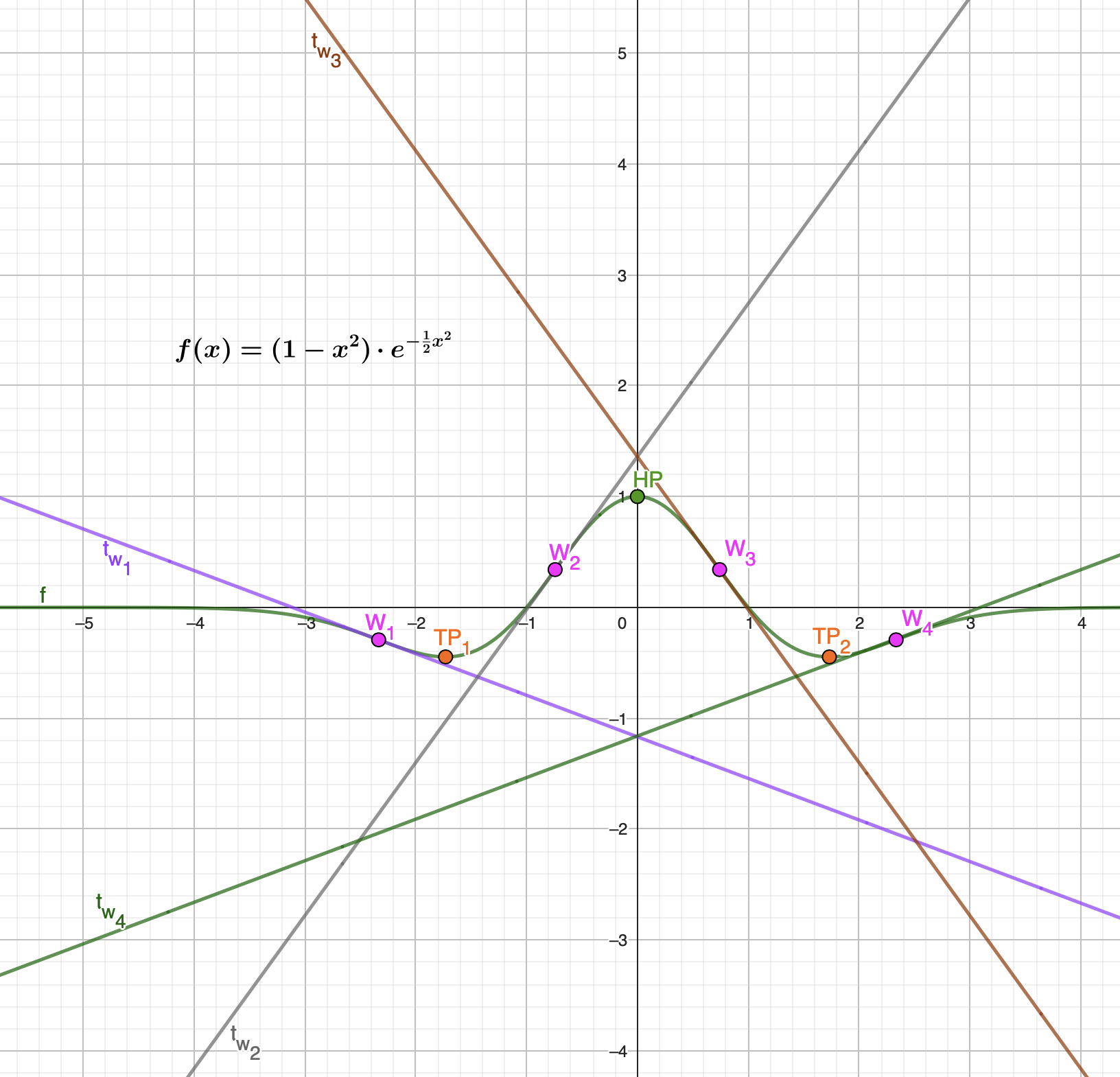
$f(x)=(1-x^2)\cdot e^{ -\frac{1}{2}x^2}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ Df=\forall x \begin{cases} (1-x^2) \in\mathbb{R}\\ \\ e^{-\frac{1}{2}x^2} \in\mathbb{R}\\ \end{cases} \longrightarrow \underline{Df=]-\infty;+\infty[} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ Wf=\forall y \in \mathbb{R}, -\infty < y < +\infty \longrightarrow \underline{Wf=]-\infty;+\infty[} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $ f(x)=(1-x^2)\cdot e^{-\frac{1}{2}x^2} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime}(x)=u^{\prime}(x) \cdot v(x) + u(x)\cdot v^{\prime}(x) | \begin{cases} u(x)=(1-x^2) \longrightarrow u^{\prime}(x)=-2x\\ \\ v(x)=e^{-\frac{1}{2}x^2} \longrightarrow v^{\prime}(x)=-x \cdot e^{-\frac{1}{2}x^2} \end{cases} $
$\qquad\qquad$ $ f^{\prime}(x)=-2x\cdot e^{-\frac{1}{2}x^2} + (1-x^2)\cdot (-x\cdot e^{-\frac{1}{2}x^2}) $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =e^{-\frac{1}{2}x^2} [-2x+(1-x^2)\cdot (-x)] $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =\underline{e^{-\frac{1}{2}x^2} (-3x+x^3)} $
$\qquad\:\:$ Zweite Ableitung:
$\qquad\qquad$ $ f^{\prime}(x)=e^{-\frac{1}{2}x^2} \cdot (-3x+x^3) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^{\prime}(x) \cdot v(x) + u(x)\cdot v^{\prime}(x) | \begin{cases} u(x)=e^{-\frac{1}{2}x^2} \longrightarrow u^{\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\\ \\ v(x)=(-3x+x^3) \longrightarrow v^{\prime}(x)=-3+3x^2 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\cdot (-3x+x^3) + e^{-\frac{1}{2}x^2}\cdot (-3+3x^2) $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =e^{-\frac{1}{2}x^2}\cdot [3x^2-x^4+(-3+3x^2)] $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =\underline{e^{-\frac{1}{2}x^2}\cdot (-x^4+6x^2-3)} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=e^{-\frac{1}{2}x^2}\cdot (-x^4+6x^2-3) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)= \begin{cases} u(x)=e^{-\frac{1}{2}x^2} \longrightarrow u^{\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\\ \\ v(x)=(-x^4+6x^2-3) \longrightarrow v^{\prime}(x)=-4x^3+12x \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\cdot (-x^4+6x^2-3) + (-4x^3+12x)\cdot e^{-\frac{1}{2}x^2} $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\:$ $ =e^{-\frac{1}{2}x^2}\cdot [x^5-6x^3+3x+(-4x^3+12x)] $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\:$ $ =\underline{e^{-\frac{1}{2}x^2}\cdot (x^5-10x^3+15x)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=(1-0^2)\cdot e^{-\frac{1}{2}0^2}=e \longrightarrow \underline{S_y(0|1)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\: (Schnittpunkt\: mit\: der\: x-Achse:\: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0 \iff (1-x^2)\cdot e^{-\frac{1}{2}x^2}=0 \Longrightarrow \begin{cases} (1-x^2)=0\:\: \textcolor{red}{|-1} \longrightarrow x=\pm1\\ \\ e^{-\frac{1}{2}x^2}=0\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Es gibt Nullstellen an der Stellen $N_1(-1|0)$ und $N_2(+1|0)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=[1-(-x)^2]\cdot e^{-\frac{1}{2}(-x)^2} =(1-x^2)\cdot e^{-\frac{1}{2}x^2} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ = f(x) \longrightarrow$ Achsensymmetrie
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkten\: untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $f^\prime(x)=0,\: f^{\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^{\prime}(x)=0 \iff e^{-\frac{1}{2}x^2}\cdot (-3x+x^3)=0 \iff \begin{cases} e^{-\frac{1}{2}x^2}=0\: \textcolor{red}{n.L.}\\ \\ (-3x+x^3)=0 \end{cases} $
$\qquad\qquad$ $ x\cdot (-3+x^2)=0 \longrightarrow \begin{cases} x=0\\ \\ (-3+x^2)=0\: \textcolor{red}{|+3} \longrightarrow x=\pm1,732 \end{cases} $
$\qquad\qquad$ Mögliche Extremspunkten bei $x_1=-1,732$, $x_2=0$ und $x_3=+1,732$
$\qquad\qquad$ Nullstellen der ersten Ableitung in zweite einsetzen:
$\qquad\qquad$ $ \begin{cases} f^{\prime\prime}(-1,732)=1,339>0 \longrightarrow ein\: Tiefpunkt\:|\: \underline{TP_1=(-1,732|-0,446)}\\ \\ f^{\prime\prime}(0)=-3<0 \longrightarrow ein\: Hochpunkt\:|\: \underline{HP=(0|1)}\\ \\ f^{\prime\prime}(+1,732)=1,339>0 \longrightarrow ein\: Tiefpunkt\:|\: \underline{TP_2=(1,732|-0,446)} \end{cases} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0,\: f^{\prime\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^{\prime\prime}(x)=0 \iff \begin{cases} e^{-\frac{1}{2}x^2}=0\: \textcolor{red}{n.L.}\\ \\ (-x^4+6x^2-3)=0\: Mit \: Substitution\: lösen: \begin{cases} x_1=-2,334\\ \\ x_2=-0,742\\ \\ x_3=0,742\\ \\ x_4=2,334 \end{cases} \end{cases} $
$\qquad\qquad$ Mögliche Wendepunkte bei:
$\qquad\qquad\qquad$ $x_{w_1}=-2,334$, $x_{w_2}=-0,742$, $x_{w_3}=0,742$ und $x_{w_4}=2,334$
$\qquad\qquad$ Nullstellen der zweite Ableitung in dritte einsetzen:
$\qquad$ $ \begin{cases} f^{\prime\prime\prime}(-2,334)=1,5>0\longrightarrow \underline{W_1(-2,334|-0,292)}, Recht-Links-Wendepunkt\\ \\ f^{\prime\prime\prime}(-0,742)=-5,52<0\longrightarrow \underline{W_2(-0,742|0,341)}, Links-Recht-Wendepunkt\\ \\ f^{\prime\prime\prime}(0,742)=5,52>0\longrightarrow \underline{W_3(0,742|0,341)}, Recht-Links-Wendepunkt\\ \\ f^{\prime\prime\prime}(2,334)=-1,5<0\longrightarrow \underline{W_4(2,334|-0,292)}, Links-Recht-Wendepunkt \end{cases} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w_1}: f^{\prime}(x_{w_1})\cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=-2,334\\ \\ f^{\prime}(x_{w_1})=-0,375\\ \\ f(x_{w_1})=-0,292 \end{cases} $
$\qquad\qquad$ $ t_{w_1}=-0,375(x+2,334)-0,292=\underline{-0,375x-1,167} $
$\qquad\qquad$ $ t_{w_2}: f^{\prime}(x_{w_2})\cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=-0,742\\ \\ f^{\prime}(x_{w_2})=1,38\\ \\ f(x_{w_2})=0,341 \end{cases} $
$\qquad\qquad$ $ t_{w_2}=1,38(x+0,742)+0,341=\underline{1,38x+1,36} $
$\qquad\qquad$ $ t_{w_3}: f^{\prime}(x_{w_3})\cdot (x-x_{w_3})+f(x_{w_3}) $ mit $ \begin{cases} x_{w_3}=0,742\\ \\ f^{\prime}(x_{w_3})=-1,38\\ \\ f(x_{w_3})=0,341 \end{cases} $
$\qquad\qquad$ $ t_{w_3}=-1,38(x-0,742)+0,341=\underline{-1,38x+1,36} $
$\qquad\qquad$ $ t_{w_4}: f^{\prime}(x_{w_4})\cdot (x-x_{w_4})+f(x_{w_4}) $ mit $ \begin{cases} x_{w_4}=2,334\\ \\ f^{\prime}(x_{w_4})=0,375\\ \\ f(x_{w_4})=-0,292 \end{cases} $
$\qquad\qquad$ $ t_{w_4}=0,375(x-2,334)-0,292=\underline{0,375x-1,167} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=0 \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ Df=\forall x \begin{cases} (1-x^2) \in\mathbb{R}\\ \\ e^{-\frac{1}{2}x^2} \in\mathbb{R}\\ \end{cases} \longrightarrow \underline{Df=]-\infty;+\infty[} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ Wf=\forall y \in \mathbb{R}, -\infty < y < +\infty \longrightarrow \underline{Wf=]-\infty;+\infty[} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $ f(x)=(1-x^2)\cdot e^{-\frac{1}{2}x^2} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime}(x)=u^{\prime}(x) \cdot v(x) + u(x)\cdot v^{\prime}(x) | \begin{cases} u(x)=(1-x^2) \longrightarrow u^{\prime}(x)=-2x\\ \\ v(x)=e^{-\frac{1}{2}x^2} \longrightarrow v^{\prime}(x)=-x \cdot e^{-\frac{1}{2}x^2} \end{cases} $
$\qquad\qquad$ $ f^{\prime}(x)=-2x\cdot e^{-\frac{1}{2}x^2} + (1-x^2)\cdot (-x\cdot e^{-\frac{1}{2}x^2}) $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =e^{-\frac{1}{2}x^2} [-2x+(1-x^2)\cdot (-x)] $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =\underline{e^{-\frac{1}{2}x^2} (-3x+x^3)} $
$\qquad\:\:$ Zweite Ableitung:
$\qquad\qquad$ $ f^{\prime}(x)=e^{-\frac{1}{2}x^2} \cdot (-3x+x^3) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^{\prime}(x) \cdot v(x) + u(x)\cdot v^{\prime}(x) | \begin{cases} u(x)=e^{-\frac{1}{2}x^2} \longrightarrow u^{\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\\ \\ v(x)=(-3x+x^3) \longrightarrow v^{\prime}(x)=-3+3x^2 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\cdot (-3x+x^3) + e^{-\frac{1}{2}x^2}\cdot (-3+3x^2) $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =e^{-\frac{1}{2}x^2}\cdot [3x^2-x^4+(-3+3x^2)] $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =\underline{e^{-\frac{1}{2}x^2}\cdot (-x^4+6x^2-3)} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=e^{-\frac{1}{2}x^2}\cdot (-x^4+6x^2-3) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)= \begin{cases} u(x)=e^{-\frac{1}{2}x^2} \longrightarrow u^{\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\\ \\ v(x)=(-x^4+6x^2-3) \longrightarrow v^{\prime}(x)=-4x^3+12x \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\cdot (-x^4+6x^2-3) + (-4x^3+12x)\cdot e^{-\frac{1}{2}x^2} $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\:$ $ =e^{-\frac{1}{2}x^2}\cdot [x^5-6x^3+3x+(-4x^3+12x)] $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\:$ $ =\underline{e^{-\frac{1}{2}x^2}\cdot (x^5-10x^3+15x)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=(1-0^2)\cdot e^{-\frac{1}{2}0^2}=e \longrightarrow \underline{S_y(0|1)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\: (Schnittpunkt\: mit\: der\: x-Achse:\: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0 \iff (1-x^2)\cdot e^{-\frac{1}{2}x^2}=0 \Longrightarrow \begin{cases} (1-x^2)=0\:\: \textcolor{red}{|-1} \longrightarrow x=\pm1\\ \\ e^{-\frac{1}{2}x^2}=0\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Es gibt Nullstellen an der Stellen $N_1(-1|0)$ und $N_2(+1|0)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=[1-(-x)^2]\cdot e^{-\frac{1}{2}(-x)^2} =(1-x^2)\cdot e^{-\frac{1}{2}x^2} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ = f(x) \longrightarrow$ Achsensymmetrie
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkten\: untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $f^\prime(x)=0,\: f^{\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^{\prime}(x)=0 \iff e^{-\frac{1}{2}x^2}\cdot (-3x+x^3)=0 \iff \begin{cases} e^{-\frac{1}{2}x^2}=0\: \textcolor{red}{n.L.}\\ \\ (-3x+x^3)=0 \end{cases} $
$\qquad\qquad$ $ x\cdot (-3+x^2)=0 \longrightarrow \begin{cases} x=0\\ \\ (-3+x^2)=0\: \textcolor{red}{|+3} \longrightarrow x=\pm1,732 \end{cases} $
$\qquad\qquad$ Mögliche Extremspunkten bei $x_1=-1,732$, $x_2=0$ und $x_3=+1,732$
$\qquad\qquad$ Nullstellen der ersten Ableitung in zweite einsetzen:
$\qquad\qquad$ $ \begin{cases} f^{\prime\prime}(-1,732)=1,339>0 \longrightarrow ein\: Tiefpunkt\:|\: \underline{TP_1=(-1,732|-0,446)}\\ \\ f^{\prime\prime}(0)=-3<0 \longrightarrow ein\: Hochpunkt\:|\: \underline{HP=(0|1)}\\ \\ f^{\prime\prime}(+1,732)=1,339>0 \longrightarrow ein\: Tiefpunkt\:|\: \underline{TP_2=(1,732|-0,446)} \end{cases} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0,\: f^{\prime\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^{\prime\prime}(x)=0 \iff \begin{cases} e^{-\frac{1}{2}x^2}=0\: \textcolor{red}{n.L.}\\ \\ (-x^4+6x^2-3)=0\: Mit \: Substitution\: lösen: \begin{cases} x_1=-2,334\\ \\ x_2=-0,742\\ \\ x_3=0,742\\ \\ x_4=2,334 \end{cases} \end{cases} $
$\qquad\qquad$ Mögliche Wendepunkte bei:
$\qquad\qquad\qquad$ $x_{w_1}=-2,334$, $x_{w_2}=-0,742$, $x_{w_3}=0,742$ und $x_{w_4}=2,334$
$\qquad\qquad$ Nullstellen der zweite Ableitung in dritte einsetzen:
$\qquad$ $ \begin{cases} f^{\prime\prime\prime}(-2,334)=1,5>0\longrightarrow \underline{W_1(-2,334|-0,292)}, Recht-Links-Wendepunkt\\ \\ f^{\prime\prime\prime}(-0,742)=-5,52<0\longrightarrow \underline{W_2(-0,742|0,341)}, Links-Recht-Wendepunkt\\ \\ f^{\prime\prime\prime}(0,742)=5,52>0\longrightarrow \underline{W_3(0,742|0,341)}, Recht-Links-Wendepunkt\\ \\ f^{\prime\prime\prime}(2,334)=-1,5<0\longrightarrow \underline{W_4(2,334|-0,292)}, Links-Recht-Wendepunkt \end{cases} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w_1}: f^{\prime}(x_{w_1})\cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=-2,334\\ \\ f^{\prime}(x_{w_1})=-0,375\\ \\ f(x_{w_1})=-0,292 \end{cases} $
$\qquad\qquad$ $ t_{w_1}=-0,375(x+2,334)-0,292=\underline{-0,375x-1,167} $
$\qquad\qquad$ $ t_{w_2}: f^{\prime}(x_{w_2})\cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=-0,742\\ \\ f^{\prime}(x_{w_2})=1,38\\ \\ f(x_{w_2})=0,341 \end{cases} $
$\qquad\qquad$ $ t_{w_2}=1,38(x+0,742)+0,341=\underline{1,38x+1,36} $
$\qquad\qquad$ $ t_{w_3}: f^{\prime}(x_{w_3})\cdot (x-x_{w_3})+f(x_{w_3}) $ mit $ \begin{cases} x_{w_3}=0,742\\ \\ f^{\prime}(x_{w_3})=-1,38\\ \\ f(x_{w_3})=0,341 \end{cases} $
$\qquad\qquad$ $ t_{w_3}=-1,38(x-0,742)+0,341=\underline{-1,38x+1,36} $
$\qquad\qquad$ $ t_{w_4}: f^{\prime}(x_{w_4})\cdot (x-x_{w_4})+f(x_{w_4}) $ mit $ \begin{cases} x_{w_4}=2,334\\ \\ f^{\prime}(x_{w_4})=0,375\\ \\ f(x_{w_4})=-0,292 \end{cases} $
$\qquad\qquad$ $ t_{w_4}=0,375(x-2,334)-0,292=\underline{0,375x-1,167} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=0 \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $

$f(x)=e^{-3x}\cdot (2x-4)$
Lösung
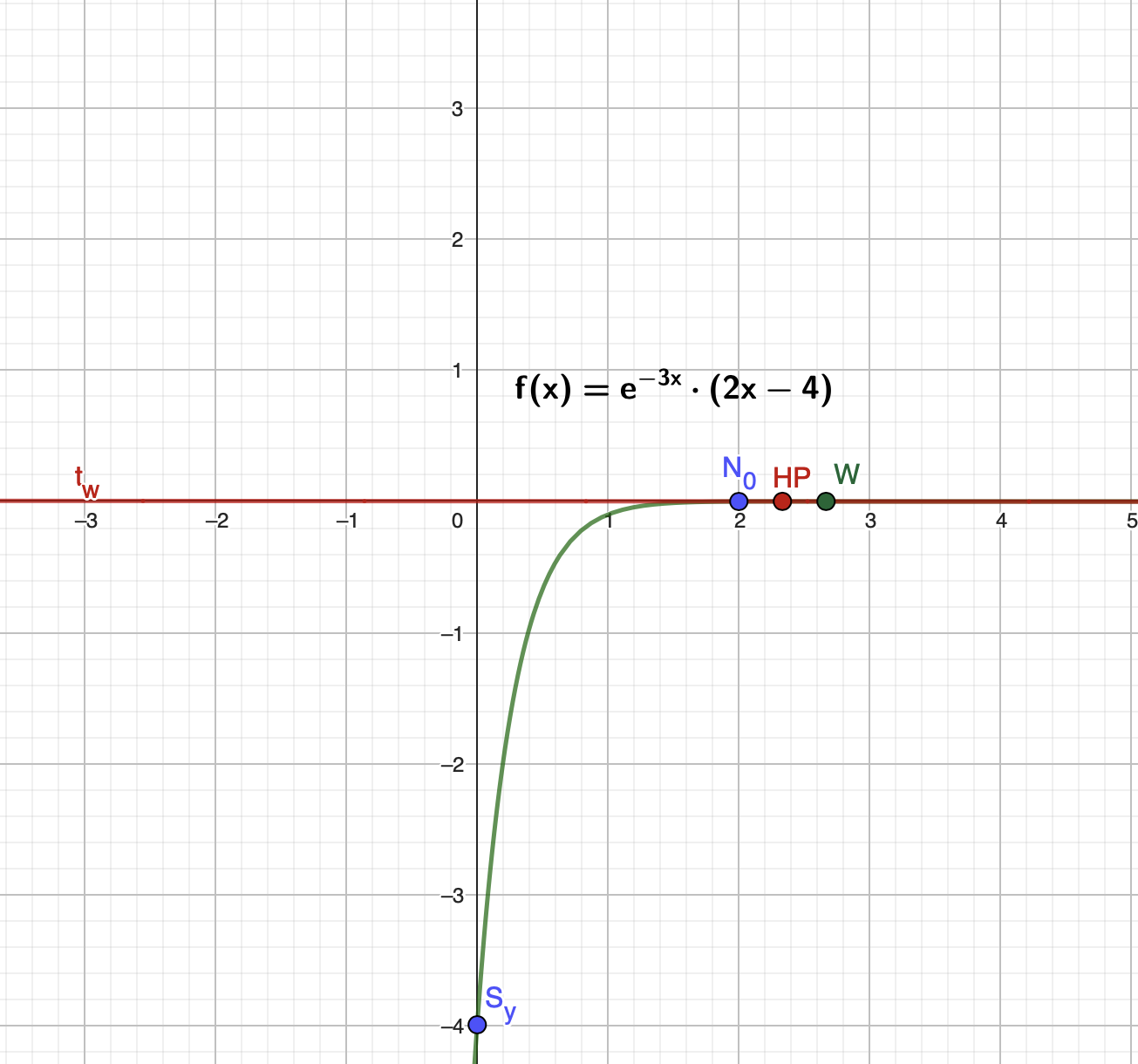
$f(x)=e^{-3x}\cdot (2x-4)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ Df=\forall x \begin{cases} e^{-3x} \in \mathbb{R}\\ \\ (2x-4) \in \mathbb{R} \end{cases} \:\: \longrightarrow \underline { Df= ]-\infty;\infty[ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ Wf=\forall y \in \mathbb{R}$, $-\infty < y \leq \frac{2}{3e^7} \longrightarrow \underline {Wf=]-\infty;\frac{2}{3e^7}]} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $f(x)=e^{-3x}\cdot (2x-4)$
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)= u^\prime(x)\cdot v(x)+ u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=e^{-3x} \longrightarrow u^\prime(x)=-3e^{-3x}\\ \\ v(x)=(2x-4) \longrightarrow v^\prime(x)=2 \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=-3e^{-3x}\cdot (2x-4)+e^{-3x}\cdot 2 $
$\qquad\qquad\qquad\:$ $ =e^{-3x}\cdot [-3(2x-4)+2] $
$\qquad\qquad\qquad\:$ $ =\underline{e^{-3x}\cdot (-6x+14)} $
$\qquad\:\:$ zweite Ableitung:
$\qquad\qquad$ $f^\prime(x)=e^{-3x}\cdot (-6x+14)$
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)= u^\prime(x)\cdot v(x)+ u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=e^{-3x} \longrightarrow u^\prime(x)=-3e^{-3x}\\ \\ v(x)=(-6x+14) \longrightarrow v^\prime(x)=-6 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-3e^{-3x}\cdot (-6x+14)+e^{-3x}\cdot (-6) $
$\qquad\qquad\qquad\:\:\:$ $ =e^{-3x}\cdot [-3(-6x+14)+(-6)] $
$\qquad\qquad\qquad\:\:\:$ $ =\underline{e^{-3x}\cdot (18x-48)} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ $f^{\prime\prime}(x)=e^{-3x}\cdot (18x-48)$
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)= u^\prime(x)\cdot v(x)+ u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=e^{-3x} \longrightarrow u^\prime(x)=-3e^{-3x}\\ \\ v(x)=(18x-48) \longrightarrow v^\prime(x)=18 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=-3e^{-3x}\cdot (18x-48)+e^{-3x}\cdot (18) $
$\qquad\qquad\qquad\:\:\:$ $ =e^{-3x}\cdot [-3(18x-48)+(18)] $
$\qquad\qquad\qquad\:\:\:$ $ =\underline{e^{-3x}\cdot (-54x+162)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=e^{-3(0)}\cdot [2(0)-4]=-4 \longrightarrow \underline{S_y(0|-4)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\: (Schnittpunkt\: mit\: der\: x-Achse:\: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0 \iff e^{-3x}\cdot (2x-4)=0 \Longrightarrow \begin{cases} e^{-3x}=0\: \textcolor{red}{n.L.}\\ \\ (2x-4)=0\: \textcolor{red}{|(+4),\: (:2)} \longrightarrow x_0=2 \end{cases} $
$\qquad\:\:$ Es gibt eine Nullstelle an der Stelle $\underline{N_0(2|0)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=e^{-3(-x)}\cdot [2(-x)-4]=e^{3x}\cdot (-2x-4) $
$\qquad\qquad\:\:\:\:\:\:$ $ \ne f(x) \longrightarrow$ kein Achsensymmetrie zur y-Achse
$\qquad\qquad\:\:\:\:\:\:$ $ \ne -f(x) \longrightarrow$ kein Punktsymmetrie zum Ursprung
$\qquad\:\:$ $f(x)= e^{-3x}\cdot (2x-4)$ ist weder achsensymmetrisch noch punktsymmetrisch.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkten\: Untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $ f^\prime(x)=0, f^{\prime\prime}(x)\ne0 $
$\qquad\qquad$ $ f^\prime(x)=0 \iff e^{-3x}\cdot (-6x+14)=0 \iff \begin{cases} e^{-3x}=0\: \textcolor{red}{n.L.}\\ \\ (-6x+14)=0\: \textcolor{red}{|(-14)} \longrightarrow x_1=\frac{7}{3} \end{cases} $
$\qquad\qquad$ Möglicher Extremspunkt bei $x_1=\frac{7}{3}$
$\qquad\qquad$ Nullstelle der ersten Ableitung in zweite einsetzen:
$\qquad\qquad$ $ f^{\prime\prime}(\frac{7}{3})= e^{-3(\frac{7}{3})}\cdot [18(\frac{7}{3})-48]=-0,005<0 \longrightarrow Hochpunkt $
$\qquad\qquad$ Der Hochpunkt beträgt: $ HP[\frac{7}{3}|f(\frac{7}{3})]=\underline{(\frac{7}{3}|\frac{2}{3e^7})} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkten\: Untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0$, $f^{\prime\prime\prime}(x)\ne0$
$\qquad\qquad$ $ f^{\prime\prime}(x)=0 \iff \begin{cases} e^{-3x}=0\: \textcolor{red}{n.L.}\\ \\ (18x-48)=0\: \textcolor{red}{|(+48)} \longrightarrow x_2=\frac{8}{3} \end{cases} $
$\qquad\qquad$ Möglicher Wendepunkt bei $x_w=\frac{8}{3}$
$\qquad\qquad$ Nullstelle der zweiten Ableitung in dritte einsetzen:
$\qquad\qquad$ $ f^{\prime\prime\prime}(\frac{8}{3})=00060>0 \longrightarrow Recht-Links-Wendepunkt $
$\qquad\qquad$ Der Wendepunkt beträgt: $W[\frac{8}{3}|f(\frac{8}{3})]=\underline{(\frac{8}{3}|\frac{4}{3e^8})}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w}:f^\prime(x_w)\cdot (x-x_w)+f(x_w) $ mit $ \begin{cases} x_w=\frac{8}{3}\\ \\ f^\prime(\frac{8}{3})=-\frac{2}{e^8}\\ \\ f(\frac{8}{3})=\frac{4}{3e^8} \end{cases} $
$\qquad\qquad$ $ t_{w}=-\frac{2}{e^8}(x-\frac{8}{3})+ \frac{4}{3e^8}=\underline{-\frac{2}{e^8}x+\frac{20}{3e^8}} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=-\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ Df=\forall x \begin{cases} e^{-3x} \in \mathbb{R}\\ \\ (2x-4) \in \mathbb{R} \end{cases} \:\: \longrightarrow \underline { Df= ]-\infty;\infty[ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ Wf=\forall y \in \mathbb{R}$, $-\infty < y \leq \frac{2}{3e^7} \longrightarrow \underline {Wf=]-\infty;\frac{2}{3e^7}]} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $f(x)=e^{-3x}\cdot (2x-4)$
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)= u^\prime(x)\cdot v(x)+ u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=e^{-3x} \longrightarrow u^\prime(x)=-3e^{-3x}\\ \\ v(x)=(2x-4) \longrightarrow v^\prime(x)=2 \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=-3e^{-3x}\cdot (2x-4)+e^{-3x}\cdot 2 $
$\qquad\qquad\qquad\:$ $ =e^{-3x}\cdot [-3(2x-4)+2] $
$\qquad\qquad\qquad\:$ $ =\underline{e^{-3x}\cdot (-6x+14)} $
$\qquad\:\:$ zweite Ableitung:
$\qquad\qquad$ $f^\prime(x)=e^{-3x}\cdot (-6x+14)$
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)= u^\prime(x)\cdot v(x)+ u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=e^{-3x} \longrightarrow u^\prime(x)=-3e^{-3x}\\ \\ v(x)=(-6x+14) \longrightarrow v^\prime(x)=-6 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-3e^{-3x}\cdot (-6x+14)+e^{-3x}\cdot (-6) $
$\qquad\qquad\qquad\:\:\:$ $ =e^{-3x}\cdot [-3(-6x+14)+(-6)] $
$\qquad\qquad\qquad\:\:\:$ $ =\underline{e^{-3x}\cdot (18x-48)} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ $f^{\prime\prime}(x)=e^{-3x}\cdot (18x-48)$
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)= u^\prime(x)\cdot v(x)+ u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=e^{-3x} \longrightarrow u^\prime(x)=-3e^{-3x}\\ \\ v(x)=(18x-48) \longrightarrow v^\prime(x)=18 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=-3e^{-3x}\cdot (18x-48)+e^{-3x}\cdot (18) $
$\qquad\qquad\qquad\:\:\:$ $ =e^{-3x}\cdot [-3(18x-48)+(18)] $
$\qquad\qquad\qquad\:\:\:$ $ =\underline{e^{-3x}\cdot (-54x+162)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=e^{-3(0)}\cdot [2(0)-4]=-4 \longrightarrow \underline{S_y(0|-4)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\: (Schnittpunkt\: mit\: der\: x-Achse:\: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0 \iff e^{-3x}\cdot (2x-4)=0 \Longrightarrow \begin{cases} e^{-3x}=0\: \textcolor{red}{n.L.}\\ \\ (2x-4)=0\: \textcolor{red}{|(+4),\: (:2)} \longrightarrow x_0=2 \end{cases} $
$\qquad\:\:$ Es gibt eine Nullstelle an der Stelle $\underline{N_0(2|0)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=e^{-3(-x)}\cdot [2(-x)-4]=e^{3x}\cdot (-2x-4) $
$\qquad\qquad\:\:\:\:\:\:$ $ \ne f(x) \longrightarrow$ kein Achsensymmetrie zur y-Achse
$\qquad\qquad\:\:\:\:\:\:$ $ \ne -f(x) \longrightarrow$ kein Punktsymmetrie zum Ursprung
$\qquad\:\:$ $f(x)= e^{-3x}\cdot (2x-4)$ ist weder achsensymmetrisch noch punktsymmetrisch.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkten\: Untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $ f^\prime(x)=0, f^{\prime\prime}(x)\ne0 $
$\qquad\qquad$ $ f^\prime(x)=0 \iff e^{-3x}\cdot (-6x+14)=0 \iff \begin{cases} e^{-3x}=0\: \textcolor{red}{n.L.}\\ \\ (-6x+14)=0\: \textcolor{red}{|(-14)} \longrightarrow x_1=\frac{7}{3} \end{cases} $
$\qquad\qquad$ Möglicher Extremspunkt bei $x_1=\frac{7}{3}$
$\qquad\qquad$ Nullstelle der ersten Ableitung in zweite einsetzen:
$\qquad\qquad$ $ f^{\prime\prime}(\frac{7}{3})= e^{-3(\frac{7}{3})}\cdot [18(\frac{7}{3})-48]=-0,005<0 \longrightarrow Hochpunkt $
$\qquad\qquad$ Der Hochpunkt beträgt: $ HP[\frac{7}{3}|f(\frac{7}{3})]=\underline{(\frac{7}{3}|\frac{2}{3e^7})} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkten\: Untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0$, $f^{\prime\prime\prime}(x)\ne0$
$\qquad\qquad$ $ f^{\prime\prime}(x)=0 \iff \begin{cases} e^{-3x}=0\: \textcolor{red}{n.L.}\\ \\ (18x-48)=0\: \textcolor{red}{|(+48)} \longrightarrow x_2=\frac{8}{3} \end{cases} $
$\qquad\qquad$ Möglicher Wendepunkt bei $x_w=\frac{8}{3}$
$\qquad\qquad$ Nullstelle der zweiten Ableitung in dritte einsetzen:
$\qquad\qquad$ $ f^{\prime\prime\prime}(\frac{8}{3})=00060>0 \longrightarrow Recht-Links-Wendepunkt $
$\qquad\qquad$ Der Wendepunkt beträgt: $W[\frac{8}{3}|f(\frac{8}{3})]=\underline{(\frac{8}{3}|\frac{4}{3e^8})}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w}:f^\prime(x_w)\cdot (x-x_w)+f(x_w) $ mit $ \begin{cases} x_w=\frac{8}{3}\\ \\ f^\prime(\frac{8}{3})=-\frac{2}{e^8}\\ \\ f(\frac{8}{3})=\frac{4}{3e^8} \end{cases} $
$\qquad\qquad$ $ t_{w}=-\frac{2}{e^8}(x-\frac{8}{3})+ \frac{4}{3e^8}=\underline{-\frac{2}{e^8}x+\frac{20}{3e^8}} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=-\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $

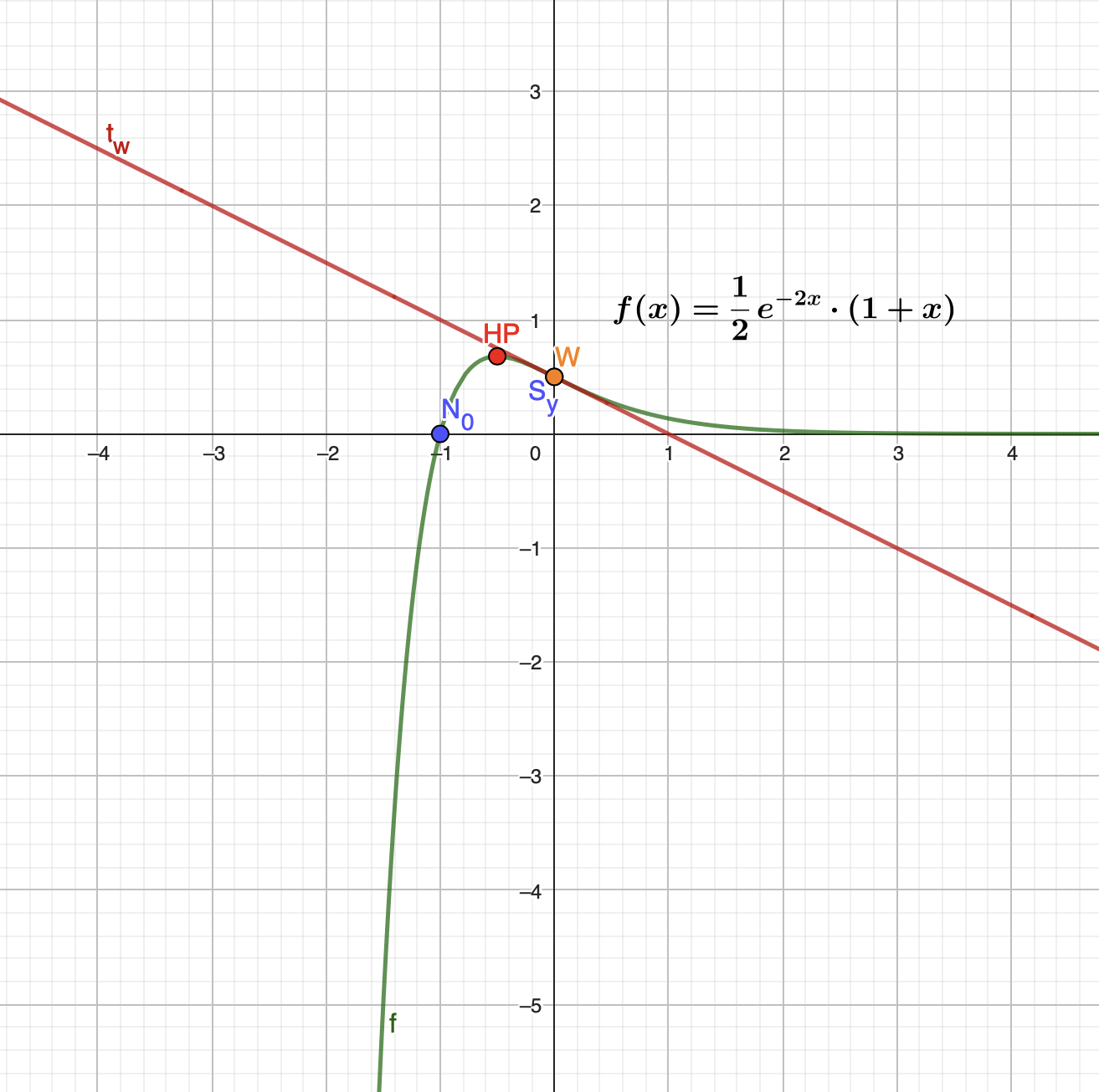
$f(x)=\frac{1}{2}e^{-2x}\cdot (1+x)$
Lösung
$f(x)=\frac{1}{2}e^{-2x}\cdot (1+x)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ Df=\forall x \begin{cases} \frac{1}{2}e^{-2x}\: \in \mathbb{R}\\ \\ (1+x)\: \in \mathbb{R} \end{cases} \longrightarrow Df=]-\infty;+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ Wf=\forall y \in \mathbb{R}, -\infty < y \leq \frac{e}{4} \longrightarrow Wf=]-\infty;\frac{e}{4}] $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $ f(x)=\frac{1}{2}e^{-2x}\cdot (1+x) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=\frac{1}{2}e^{-2x} \longrightarrow u^\prime(x)=-e^{-2x}\\ \\ v(x)=(1+x) \longrightarrow v^\prime(x)=1 \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=-e^{-2x}\cdot (1+x)+\frac{1}{2}e^{-2x}\cdot (1) $
$\qquad\qquad\qquad\:$ $ =e^{-2x}[-(1+x)+\frac{1}{2}] $
$\qquad\qquad\qquad\:$ $ =\underline{-e^{-2x}(\frac{1}{2}+x)} $
$\qquad\:\:$ Zweite Ableitung:
$\qquad\qquad$ $ f^\prime(x)=-e^{-2x}(\frac{1}{2}+x) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=-e^{-2x} \longrightarrow u^\prime(x)=2e^{-2x}\\ \\ v(x)=(\frac{1}{2}+x) \longrightarrow v^\prime(x)=1 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=[2e^{-2x}\cdot (\frac{1}{2}+x)+(-e^{-2x})\cdot (1)] $
$\qquad\qquad\qquad\:\:$ $ =e^{-2x}[2\cdot(\frac{1}{2}+x)+(-1)] $
$\qquad\qquad\qquad\:\:$ $ =\underline{2x\cdot e^{-2x}} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ $ f^{\prime\prime}(x)=2x\cdot e^{-2x} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=2x \longrightarrow u^\prime(x)=2\\ \\ v(x)=e^{-2x} \longrightarrow v^\prime(x)=-2e^{-2x} \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=[2\cdot e^{-2x}+2x\cdot (-2e^{-2x})] $
$\qquad\qquad\qquad\:\:$ $ =2e^{-2x}\cdot (1-2x) $
$\qquad\qquad\qquad\:\:$ $ =\underline{2e^{-2x}\cdot (1-2x)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkte\: mit\: der\: y-Achse: S_y[0|f(0)] $
$\qquad\:\:$ $ f(0)=\frac{1}{2}e^{-2(0)}\cdot [1+(0)]=\frac{1}{2} \longrightarrow \underline{S_y(0|\frac{1}{2})} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\: (Schnittpunkte\: mit\: der\: x-Achse: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0 \iff \frac{1}{2} e^{-2x} \cdot (1+x)=0 \Longrightarrow \begin{cases} \frac{1}{2}e^{-2x}=0\: \textcolor{red}{n.L.}\\ \\ (1+x)=0\: \textcolor{red}{|\: -(1)} \longrightarrow x_0=-1 \end{cases} $
$\qquad\:\:$ Es gibt eine Nullstelle an der Stelle $\underline{N_0=(-1|0)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=\frac{1}{2}e^{-2(-x)}\cdot [1+(-x)] =\frac{1}{2}e^{2x}\cdot (1-x) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ \ne f(x) \longrightarrow$ keine Achsensymmetrie
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ \ne -f(x) \longrightarrow$ keine Punktsymmetrie
$\qquad\:\:$ $ f(x)=\frac{1}{2}e^{-2x}\cdot (1+x)$ ist weder achsensymmetrisch noch punktsymmetrisch.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkte\: untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $f^\prime(x)=0,\: f^{\prime\prime}(x)\ne0$
$\qquad\:\:$ $ f^\prime(x)=0 \iff -e^{-2x}\cdot (\frac{1}{2}+x)=0 \iff \begin{cases} -e^{-2x}=0\: \textcolor{red}{n.L.}\\ \\ (\frac{1}{2}+x)=0 \textcolor{red}{|(-\frac{1}{2})} \longrightarrow x_1=-\frac{1}{2} \end{cases} $
$\qquad\:\:$ Möglicher Extremspunkt bei $x_1=-\frac{1}{2}$
$\qquad\:\:$ Nullstelle der ersten Ableitung in zweite einsetzen:
$\qquad\:\:$ $ f^{\prime\prime}(-\frac{1}{2})=2(-\frac{1}{2})\cdot e^{-2(-\frac{1}{2})}=-e<0 \longrightarrow Hochpunkt $
$\qquad\:\:$ Der Hochpunkt beträgt: $\underline{HP(-0,5|0,68)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}=0, f^{\prime\prime\prime}\ne0$
$\qquad\:\:$ $ f^{\prime\prime}=0 \iff \begin{cases} 2x=0 \longrightarrow x_2=0\\ \\ e^{-2x}=0\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Möglicher Wendepunkt bei $x_w=0$
$\qquad\:\:$ Nullstelle der zweiten Ableitung in dritte einsetzen:
$\qquad\:\:$ $ f^{\prime\prime\prime}(0)=2e^{-2(0)}\cdot [1-2(0)]=2>0 \longrightarrow Recht-Links-Wendepunkt $
$\qquad\:\:$ Der Wendepunkt beträgt: $\underline{W(0|0,5)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_w: f^\prime(x_w)\cdot (x-x_w)+f(x_w) $ mit $ \begin{cases} x_w=0\\ \\ f^\prime(0)=-\frac{1}{2}\\ \\ f(0)=\frac{1}{2} \end{cases} $
$\qquad\qquad$ $ t_w=-\frac{1}{2}(x-0)+\frac{1}{2}=\underline{-\frac{1}{2}x+\frac{1}{2}} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=-\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ Df=\forall x \begin{cases} \frac{1}{2}e^{-2x}\: \in \mathbb{R}\\ \\ (1+x)\: \in \mathbb{R} \end{cases} \longrightarrow Df=]-\infty;+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ Wf=\forall y \in \mathbb{R}, -\infty < y \leq \frac{e}{4} \longrightarrow Wf=]-\infty;\frac{e}{4}] $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $ f(x)=\frac{1}{2}e^{-2x}\cdot (1+x) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=\frac{1}{2}e^{-2x} \longrightarrow u^\prime(x)=-e^{-2x}\\ \\ v(x)=(1+x) \longrightarrow v^\prime(x)=1 \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=-e^{-2x}\cdot (1+x)+\frac{1}{2}e^{-2x}\cdot (1) $
$\qquad\qquad\qquad\:$ $ =e^{-2x}[-(1+x)+\frac{1}{2}] $
$\qquad\qquad\qquad\:$ $ =\underline{-e^{-2x}(\frac{1}{2}+x)} $
$\qquad\:\:$ Zweite Ableitung:
$\qquad\qquad$ $ f^\prime(x)=-e^{-2x}(\frac{1}{2}+x) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=-e^{-2x} \longrightarrow u^\prime(x)=2e^{-2x}\\ \\ v(x)=(\frac{1}{2}+x) \longrightarrow v^\prime(x)=1 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=[2e^{-2x}\cdot (\frac{1}{2}+x)+(-e^{-2x})\cdot (1)] $
$\qquad\qquad\qquad\:\:$ $ =e^{-2x}[2\cdot(\frac{1}{2}+x)+(-1)] $
$\qquad\qquad\qquad\:\:$ $ =\underline{2x\cdot e^{-2x}} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ $ f^{\prime\prime}(x)=2x\cdot e^{-2x} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=2x \longrightarrow u^\prime(x)=2\\ \\ v(x)=e^{-2x} \longrightarrow v^\prime(x)=-2e^{-2x} \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=[2\cdot e^{-2x}+2x\cdot (-2e^{-2x})] $
$\qquad\qquad\qquad\:\:$ $ =2e^{-2x}\cdot (1-2x) $
$\qquad\qquad\qquad\:\:$ $ =\underline{2e^{-2x}\cdot (1-2x)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkte\: mit\: der\: y-Achse: S_y[0|f(0)] $
$\qquad\:\:$ $ f(0)=\frac{1}{2}e^{-2(0)}\cdot [1+(0)]=\frac{1}{2} \longrightarrow \underline{S_y(0|\frac{1}{2})} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\: (Schnittpunkte\: mit\: der\: x-Achse: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0 \iff \frac{1}{2} e^{-2x} \cdot (1+x)=0 \Longrightarrow \begin{cases} \frac{1}{2}e^{-2x}=0\: \textcolor{red}{n.L.}\\ \\ (1+x)=0\: \textcolor{red}{|\: -(1)} \longrightarrow x_0=-1 \end{cases} $
$\qquad\:\:$ Es gibt eine Nullstelle an der Stelle $\underline{N_0=(-1|0)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=\frac{1}{2}e^{-2(-x)}\cdot [1+(-x)] =\frac{1}{2}e^{2x}\cdot (1-x) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ \ne f(x) \longrightarrow$ keine Achsensymmetrie
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ \ne -f(x) \longrightarrow$ keine Punktsymmetrie
$\qquad\:\:$ $ f(x)=\frac{1}{2}e^{-2x}\cdot (1+x)$ ist weder achsensymmetrisch noch punktsymmetrisch.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkte\: untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $f^\prime(x)=0,\: f^{\prime\prime}(x)\ne0$
$\qquad\:\:$ $ f^\prime(x)=0 \iff -e^{-2x}\cdot (\frac{1}{2}+x)=0 \iff \begin{cases} -e^{-2x}=0\: \textcolor{red}{n.L.}\\ \\ (\frac{1}{2}+x)=0 \textcolor{red}{|(-\frac{1}{2})} \longrightarrow x_1=-\frac{1}{2} \end{cases} $
$\qquad\:\:$ Möglicher Extremspunkt bei $x_1=-\frac{1}{2}$
$\qquad\:\:$ Nullstelle der ersten Ableitung in zweite einsetzen:
$\qquad\:\:$ $ f^{\prime\prime}(-\frac{1}{2})=2(-\frac{1}{2})\cdot e^{-2(-\frac{1}{2})}=-e<0 \longrightarrow Hochpunkt $
$\qquad\:\:$ Der Hochpunkt beträgt: $\underline{HP(-0,5|0,68)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}=0, f^{\prime\prime\prime}\ne0$
$\qquad\:\:$ $ f^{\prime\prime}=0 \iff \begin{cases} 2x=0 \longrightarrow x_2=0\\ \\ e^{-2x}=0\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Möglicher Wendepunkt bei $x_w=0$
$\qquad\:\:$ Nullstelle der zweiten Ableitung in dritte einsetzen:
$\qquad\:\:$ $ f^{\prime\prime\prime}(0)=2e^{-2(0)}\cdot [1-2(0)]=2>0 \longrightarrow Recht-Links-Wendepunkt $
$\qquad\:\:$ Der Wendepunkt beträgt: $\underline{W(0|0,5)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_w: f^\prime(x_w)\cdot (x-x_w)+f(x_w) $ mit $ \begin{cases} x_w=0\\ \\ f^\prime(0)=-\frac{1}{2}\\ \\ f(0)=\frac{1}{2} \end{cases} $
$\qquad\qquad$ $ t_w=-\frac{1}{2}(x-0)+\frac{1}{2}=\underline{-\frac{1}{2}x+\frac{1}{2}} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=-\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $

$f(x)=x^2\cdot e^{-x}$
Lösung
$f(x)=x^2\cdot e^{-x}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ D_f=\forall x\: \begin{cases} x^2\in \mathbb{R}\\ \\ e^{-x}\in \mathbb{R} \end{cases} \:\: \longrightarrow \:\: \underline { D_f=]-\infty;+\infty[ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertesbereich\: ermitteln $
$\qquad\:\:$ $ W_f=\forall y \in \mathbb{R}, \:0\leq y\: \longrightarrow\: \underline { W_f=[0;+\infty[ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung: $ $
$\qquad\qquad$ $ f(x)=x^2\cdot e^{-x} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\:|\:\: \begin{cases} u(x)=x^2\: \longrightarrow \: u^\prime(x)=2x\\ \\ v(x)=e^{-x}\: \longrightarrow \:v^\prime(x)=-e^{-x} \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=2x\cdot e^{-x}+ x^2\cdot (-e^{-x}) $
$\qquad\qquad\qquad\:\:$ $ =\underline{e^{-x}\cdot (2x-x^2)} $
$\qquad\:\:$ Zweite Ableitung: $ $
$\qquad\qquad$ $ f^\prime(x)=e^{-x}\cdot (2x-x^2) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\:|\:\: \begin{cases} u(x)=e^{-x}\: \longrightarrow \: u^\prime(x)=-e^{-x}\\ \\ v(x)=(2x-x^2)\: \longrightarrow \:v^\prime(x)=2-2x \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-e^{-x}\cdot (2x-x^2)+ e^{-x}\cdot (2-2x) $
$\qquad\qquad\qquad\:\:$ $ =e^{-x}\cdot [-(2x-x^2)+(2-2x)] $
$\qquad\qquad\qquad\:\:$ $ =\underline{e^{-x}\cdot (x^2-4x+2)} $
$\qquad\:\:$ Dritte Ableitung: $ $
$\qquad\qquad$ $ f^{\prime\prime}(x)=e^{-x}\cdot (x^2-4x+2) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\:|\:\: \begin{cases} u(x)=e^{-x}\: \longrightarrow \: u^\prime(x)=-e^{-x}\\ \\ v(x)=(x^2-4x+2)\: \longrightarrow \:v^\prime(x)=2x-4 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=-e^{-x}\cdot (x^2-4x+2)+ e^{-x}\cdot (2x-4) $
$\qquad\qquad\qquad\:\:$ $ =-e^{-x}\cdot [(x^2-4x+2)-(2x-4)] $
$\qquad\qquad\qquad\:\:$ $ =\underline{-e^{-x}\cdot (x^2-6x+6)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=(0)^2\cdot e^{-0}\:\longrightarrow \: \underline{S_y(0|0)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen \:(Schnittpunkte\: mit\: der\: x-Achse:\: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0) \iff x^2\cdot e^{-x}=0 \Longrightarrow \begin{cases} x^2=0\: \longrightarrow\: x=0\\ \\ e^{-x}=0\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Es gibt eine Nullstelle an der Stelle $\underline{N_0=(0|0)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=(-x)^2\cdot e^{-(-x)}=x^2\cdot e^{x} $
$\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ \neq f(x) \:\: \longrightarrow \:\: $ keine Achsensymmetrie
$\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ \neq -f(x) \:\: \longrightarrow \:\: $ keine Punktsymmetrie
$\qquad\:\:$ $ f(x)=x^2\cdot e^{-x} $ ist weder achsensymmetrisch noch punktsymmetrisch
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\:Extrempunkte\: untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $ f^\prime(x)=0,\: f^{\prime\prime}(x) \neq0 $
$\qquad\:\:$ $ f^\prime(x)=0 \iff e^{-x}\cdot (2x-x^2)= 0 \iff \begin{cases} e^{-x}=0\: \textcolor{red}{n.L.}\\ \\ (2x-x^2)=0 \longrightarrow \begin{cases} x=0\\ \\ x=2 \end{cases} \end{cases} $
$\qquad\:\:$ Möglicher Extrempunkte bei $x_1=0$ und $x_2=2$
$\qquad\:\:$ Nullstellen der ersten Ableitung in zweite einsetzen:
$\qquad\qquad$ $ f^{\prime\prime}(0)=e^{-0}\cdot [0^2-4(0)+2]=>0 \longrightarrow Tiefpunkt $
$\qquad\qquad\qquad$ Der Tiefpunkt beträgt: $\underline{TP[0|f(0)]=(0|0)}$
$\qquad\qquad$ $ f^{\prime\prime}(2)=e^{-2}\cdot [x^2-4(2)+2]=-0,27<0 \longrightarrow Hochpunkt $
$\qquad\qquad\qquad$ Der Hochpunkt beträgt: $\underline{HP[2|f(2)]=(2|0,541)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\:Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $ f^{\prime\prime}(x)=0,\: f^{\prime\prime\prime} \neq 0 $
$\qquad\:\:$ $ f^{\prime\prime}(x)=0 \iff e^{-x}\cdot (x^2-4x+2)=0 \iff \begin{cases} e^{-x}=0\: \textcolor{red}{n.L.}\\ \\ (x^2-4x+2)=0\: (mit\: pq-Formel) \end{cases} $
$\qquad\:\:$ $ x_{1/2}=-\frac{-p}{2} \pm \sqrt{(\frac{-p}{2})^2-q} = -\frac{-4}{2} \pm \sqrt{(\frac{-4}{2})^2-2} =2\pm \sqrt{2} $
$\qquad\qquad\qquad$ $ \longrightarrow \begin{cases} x_1=2-\sqrt{2}=0,58\\ \\ x_2=2+\sqrt{2}=3,41 \end{cases} $
$\qquad\:\:$ Mögliche Wendepunkte bei $x_{w_1}=0,58$ und $x_{w_2}=3,41$
$\qquad\:\:$ Nullstellen der zweiten Ableitung in dritte einsetzen:
$\qquad\qquad$ $ f^{\prime\prime\prime}(0,58)=-1,599<0 \longrightarrow Links-Recht-Wendepunkt $
$\qquad\qquad$ $ f^{\prime\prime\prime}(3,41)=85,7>0 \longrightarrow Recht-Links-Wendepunkt $
$\qquad\:\:$ Die Wendepunkte sind: $\underline{W_1(0,58|0,19)\:}$ und $\: \underline{W_2(3,41|0,38)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\:Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ Für $W_1=0,58$; $ t_{w_1}: f^\prime(x_{w_1})\cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=0,58\\ \\ f^\prime(0,58)=0,46\\ \\ f(0,58)=0,19 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_1}=0,46(x-0,58)+0,19=0,46x-0,07} $
$\qquad\qquad$ Für $W_2=3,41$; $ t_{w_2}: f^\prime(x_{w_2})\cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=3,41\\ \\ f^\prime(3,41)=-0,16\\ \\ f(3,41)=0,38 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_2}=-0,16(x-3,41)+0,38=-0,16x+0,92} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\:Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=+\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $

$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ D_f=\forall x\: \begin{cases} x^2\in \mathbb{R}\\ \\ e^{-x}\in \mathbb{R} \end{cases} \:\: \longrightarrow \:\: \underline { D_f=]-\infty;+\infty[ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertesbereich\: ermitteln $
$\qquad\:\:$ $ W_f=\forall y \in \mathbb{R}, \:0\leq y\: \longrightarrow\: \underline { W_f=[0;+\infty[ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung: $ $
$\qquad\qquad$ $ f(x)=x^2\cdot e^{-x} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\:|\:\: \begin{cases} u(x)=x^2\: \longrightarrow \: u^\prime(x)=2x\\ \\ v(x)=e^{-x}\: \longrightarrow \:v^\prime(x)=-e^{-x} \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=2x\cdot e^{-x}+ x^2\cdot (-e^{-x}) $
$\qquad\qquad\qquad\:\:$ $ =\underline{e^{-x}\cdot (2x-x^2)} $
$\qquad\:\:$ Zweite Ableitung: $ $
$\qquad\qquad$ $ f^\prime(x)=e^{-x}\cdot (2x-x^2) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\:|\:\: \begin{cases} u(x)=e^{-x}\: \longrightarrow \: u^\prime(x)=-e^{-x}\\ \\ v(x)=(2x-x^2)\: \longrightarrow \:v^\prime(x)=2-2x \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-e^{-x}\cdot (2x-x^2)+ e^{-x}\cdot (2-2x) $
$\qquad\qquad\qquad\:\:$ $ =e^{-x}\cdot [-(2x-x^2)+(2-2x)] $
$\qquad\qquad\qquad\:\:$ $ =\underline{e^{-x}\cdot (x^2-4x+2)} $
$\qquad\:\:$ Dritte Ableitung: $ $
$\qquad\qquad$ $ f^{\prime\prime}(x)=e^{-x}\cdot (x^2-4x+2) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\:|\:\: \begin{cases} u(x)=e^{-x}\: \longrightarrow \: u^\prime(x)=-e^{-x}\\ \\ v(x)=(x^2-4x+2)\: \longrightarrow \:v^\prime(x)=2x-4 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=-e^{-x}\cdot (x^2-4x+2)+ e^{-x}\cdot (2x-4) $
$\qquad\qquad\qquad\:\:$ $ =-e^{-x}\cdot [(x^2-4x+2)-(2x-4)] $
$\qquad\qquad\qquad\:\:$ $ =\underline{-e^{-x}\cdot (x^2-6x+6)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=(0)^2\cdot e^{-0}\:\longrightarrow \: \underline{S_y(0|0)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen \:(Schnittpunkte\: mit\: der\: x-Achse:\: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0) \iff x^2\cdot e^{-x}=0 \Longrightarrow \begin{cases} x^2=0\: \longrightarrow\: x=0\\ \\ e^{-x}=0\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Es gibt eine Nullstelle an der Stelle $\underline{N_0=(0|0)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=(-x)^2\cdot e^{-(-x)}=x^2\cdot e^{x} $
$\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ \neq f(x) \:\: \longrightarrow \:\: $ keine Achsensymmetrie
$\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ \neq -f(x) \:\: \longrightarrow \:\: $ keine Punktsymmetrie
$\qquad\:\:$ $ f(x)=x^2\cdot e^{-x} $ ist weder achsensymmetrisch noch punktsymmetrisch
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\:Extrempunkte\: untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $ f^\prime(x)=0,\: f^{\prime\prime}(x) \neq0 $
$\qquad\:\:$ $ f^\prime(x)=0 \iff e^{-x}\cdot (2x-x^2)= 0 \iff \begin{cases} e^{-x}=0\: \textcolor{red}{n.L.}\\ \\ (2x-x^2)=0 \longrightarrow \begin{cases} x=0\\ \\ x=2 \end{cases} \end{cases} $
$\qquad\:\:$ Möglicher Extrempunkte bei $x_1=0$ und $x_2=2$
$\qquad\:\:$ Nullstellen der ersten Ableitung in zweite einsetzen:
$\qquad\qquad$ $ f^{\prime\prime}(0)=e^{-0}\cdot [0^2-4(0)+2]=>0 \longrightarrow Tiefpunkt $
$\qquad\qquad\qquad$ Der Tiefpunkt beträgt: $\underline{TP[0|f(0)]=(0|0)}$
$\qquad\qquad$ $ f^{\prime\prime}(2)=e^{-2}\cdot [x^2-4(2)+2]=-0,27<0 \longrightarrow Hochpunkt $
$\qquad\qquad\qquad$ Der Hochpunkt beträgt: $\underline{HP[2|f(2)]=(2|0,541)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\:Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $ f^{\prime\prime}(x)=0,\: f^{\prime\prime\prime} \neq 0 $
$\qquad\:\:$ $ f^{\prime\prime}(x)=0 \iff e^{-x}\cdot (x^2-4x+2)=0 \iff \begin{cases} e^{-x}=0\: \textcolor{red}{n.L.}\\ \\ (x^2-4x+2)=0\: (mit\: pq-Formel) \end{cases} $
$\qquad\:\:$ $ x_{1/2}=-\frac{-p}{2} \pm \sqrt{(\frac{-p}{2})^2-q} = -\frac{-4}{2} \pm \sqrt{(\frac{-4}{2})^2-2} =2\pm \sqrt{2} $
$\qquad\qquad\qquad$ $ \longrightarrow \begin{cases} x_1=2-\sqrt{2}=0,58\\ \\ x_2=2+\sqrt{2}=3,41 \end{cases} $
$\qquad\:\:$ Mögliche Wendepunkte bei $x_{w_1}=0,58$ und $x_{w_2}=3,41$
$\qquad\:\:$ Nullstellen der zweiten Ableitung in dritte einsetzen:
$\qquad\qquad$ $ f^{\prime\prime\prime}(0,58)=-1,599<0 \longrightarrow Links-Recht-Wendepunkt $
$\qquad\qquad$ $ f^{\prime\prime\prime}(3,41)=85,7>0 \longrightarrow Recht-Links-Wendepunkt $
$\qquad\:\:$ Die Wendepunkte sind: $\underline{W_1(0,58|0,19)\:}$ und $\: \underline{W_2(3,41|0,38)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\:Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ Für $W_1=0,58$; $ t_{w_1}: f^\prime(x_{w_1})\cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=0,58\\ \\ f^\prime(0,58)=0,46\\ \\ f(0,58)=0,19 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_1}=0,46(x-0,58)+0,19=0,46x-0,07} $
$\qquad\qquad$ Für $W_2=3,41$; $ t_{w_2}: f^\prime(x_{w_2})\cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=3,41\\ \\ f^\prime(3,41)=-0,16\\ \\ f(3,41)=0,38 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_2}=-0,16(x-3,41)+0,38=-0,16x+0,92} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\:Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=+\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $
