Zentralabitur 2020 - Mathe Grundkurs - Teil 2 - Unternehmen
Zentralabitur 2020 – Mathe Grundkurs – Teil 2 – Unternehmen
Aufgabe 4.2. Unternehmen

Lösung 1)
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize a)\: Wahrscheinlichkeit,\: dass\: mindestens\: 17\: der\: ausgewählten\: Beschäftigten\: weiblich\: sind $
$\qquad\:\:$ $ P(X\geq17) = 1-F(50;\frac{1}{3};16)\approx0,5132\approx51,3\% $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b)\: Beschreibe\: die\: Bedeutung\: der\: folgenden\: mathematischen\: Aussage $
$\qquad\:\:$ $ \begin{pmatrix} 50\\ 13 \end{pmatrix} \large \cdot \begin{pmatrix} \frac{1}{3} \end{pmatrix} ^{13} \cdot \begin{pmatrix} \frac{2}{3} \end{pmatrix} ^{37} $ $ + \begin{pmatrix} 50\\ 14 \end{pmatrix} \large \cdot \begin{pmatrix} \frac{1}{3} \end{pmatrix} ^{14} \cdot \begin{pmatrix} \frac{2}{3} \end{pmatrix} ^{36} $ $ \approx0,158 $
$\qquad\:\:$ Die Aussage beschreibt die Wahrscheinlichkeit dafür, dass von den $50$ ausgewählten Beschäftigten
$\qquad\:\:$ $13$ oder $14$ weiblich sind, beträgt ca. $15,8\%$.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize c) $
$\qquad\:\:$ $ B(50;\frac{1}{10};10) = \begin{pmatrix} 50\\ 10 \end{pmatrix} \large \cdot \begin{pmatrix} \frac{1}{3} \end{pmatrix} ^{10} \cdot \begin{pmatrix} \frac{2}{3} \end{pmatrix} ^{40} $ $ \approx0,0157\approx1,57\% $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize d) $
$\qquad\:\:$ $ E(X)=50\cdot \large \frac{1}{3} $ $\approx16,67$
$\qquad\:\:$ Damit hat die Wahrscheinlichkeitsverteilung von $X$ ihren größten wert für eine der beiden
$\qquad\:\:$ natürlichen Zahlen, die $16,67$ benachbart sind.
Lösung 2)
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize a) \: die\: Werte\: von\: $x$\: und\: $y$ $
$\qquad\:\:$ $ x=100\%-10,5\%=89,5\%, \:\:\: y= $ $ \large \frac{1}{3} $ $ \cdot0,035\approx0,01 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b)\: Wahrscheinlichkeit\: dafür,\: dass\: sie\: nicht\: weiblich\: ist\: (Vierfeldertafel) $
$\qquad\qquad$

$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b)\: Anteil\: der\: weiblichen\: Beschäftigten $
$\qquad\qquad$ $ 5\cdot \frac{4}{100}\cdot a=\frac{1}{10} \cdot(1-a)\iff a=\frac{1}{3} $
Zentralabitur 2020 - Mathe Grundkurs - Teil 2 - Würfel
Zentralabitur 2020 – Mathe Grundkurs – Teil 2 – Würfel
Aufgabe 4.1. Würfel

Lösung a)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
a)\: Der\: 6er-Würfel\: wird\: 10-mal\: geworfen
$
$\qquad\:\:$ Berechnen die Wahrscheinlichkeit für folgende Ereignisse:
$\qquad\qquad$ $ A: $ “Bei genau 4 Würfeln wird eine 6 gewürfelt.”
$\qquad\qquad\:\:$ $ p(a)=(10; \frac{1}{3}; 4)= \begin{pmatrix} 10\\ 4 \end{pmatrix} \cdot \begin{pmatrix} \Large \frac{1}{3} \end{pmatrix} ^4 \cdot \begin{pmatrix} \Large \frac{2}{3} \end{pmatrix} ^6 \approx0,228=22,8\% $
$\qquad\qquad$ $ B: $ “Bei keinem Wurf wird eine 6 gewürfelt.”
$\qquad\qquad\:\:$ $ p(b)=(\frac{2}{3})^{10} \approx0,0173=1,73\% $
$\qquad\:\:$ Berechnen die Wahrscheinlichkeit für folgende Ereignisse:
$\qquad\qquad$ $ A: $ “Bei genau 4 Würfeln wird eine 6 gewürfelt.”
$\qquad\qquad\:\:$ $ p(a)=(10; \frac{1}{3}; 4)= \begin{pmatrix} 10\\ 4 \end{pmatrix} \cdot \begin{pmatrix} \Large \frac{1}{3} \end{pmatrix} ^4 \cdot \begin{pmatrix} \Large \frac{2}{3} \end{pmatrix} ^6 \approx0,228=22,8\% $
$\qquad\qquad$ $ B: $ “Bei keinem Wurf wird eine 6 gewürfelt.”
$\qquad\qquad\:\:$ $ p(b)=(\frac{2}{3})^{10} \approx0,0173=1,73\% $
Lösung b)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
b)\: Baumdiagramm
$
$\qquad\:\:$
$\qquad\:\:$ Wahrscheinlichkeit dafür, dass Luisa anfangen darf.
$\qquad\:\:$
$\qquad\qquad$ $ \Large P_{(bei\: höchstens\: 3\: Würfen\: eine\: 6)} = \frac{1}{3} + \frac{2}{3}\cdot \frac{1}{3} + \frac{2}{3}\cdot \frac{2}{3}\cdot \frac{1}{3} = \frac{19}{27} $
$\qquad\:\:$

$\qquad\:\:$ Wahrscheinlichkeit dafür, dass Luisa anfangen darf.
$\qquad\:\:$

$\qquad\qquad$ $ \Large P_{(bei\: höchstens\: 3\: Würfen\: eine\: 6)} = \frac{1}{3} + \frac{2}{3}\cdot \frac{1}{3} + \frac{2}{3}\cdot \frac{2}{3}\cdot \frac{1}{3} = \frac{19}{27} $
Lösung c)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
c)\: Wie\: oft\: mit\: dem\: 6er-Würfel\: mindestens\: gewürfelt\: werden\: müsste, \:…
$
$\qquad\:\:$ $ P(X\geq1)\geq0,95 \Rightarrow 1-P(X=0)\geq0,95 $
$\qquad\qquad$ $ \begin{pmatrix} \frac{2}{3} \end{pmatrix} ^n \leq\frac{5}{100} \Rightarrow n\geq \begin{pmatrix} \Large \frac{ln\frac{5}{100}}{ln\frac{2}{3}} \end{pmatrix} \approx7,39 $
$\qquad\:\:$ Es mindestens $8-mal$ gewürfelt werden, damit die Wahrscheinlichkeit mindestens eine 6 zu würfeln,
$\qquad\:\:$ mindestens $95\%$ beträgt.
$\qquad\:\:$ $ P(X\geq1)\geq0,95 \Rightarrow 1-P(X=0)\geq0,95 $
$\qquad\qquad$ $ \begin{pmatrix} \frac{2}{3} \end{pmatrix} ^n \leq\frac{5}{100} \Rightarrow n\geq \begin{pmatrix} \Large \frac{ln\frac{5}{100}}{ln\frac{2}{3}} \end{pmatrix} \approx7,39 $
$\qquad\:\:$ Es mindestens $8-mal$ gewürfelt werden, damit die Wahrscheinlichkeit mindestens eine 6 zu würfeln,
$\qquad\:\:$ mindestens $95\%$ beträgt.
Lösung d)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
d)\: Die\: Augensumme: beträgt\: 11
$
$\qquad\:\:$ $5-6$ und $6-5$ sind die beide mögliche Kombination für die Augenzahl $11$
$\qquad\qquad$ $ \Longrightarrow P(C)= \frac{1}{3} \cdot \frac{1}{3} + \frac{1}{6} \cdot \frac{1}{6} = \frac{5}{36} \approx0,1389=13,89\% $
$\qquad\:\:$ $5-6$ und $6-5$ sind die beide mögliche Kombination für die Augenzahl $11$
$\qquad\qquad$ $ \Longrightarrow P(C)= \frac{1}{3} \cdot \frac{1}{3} + \frac{1}{6} \cdot \frac{1}{6} = \frac{5}{36} \approx0,1389=13,89\% $
Lösung e)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
e)\: Zeige,\: dass\: die\: Wahrscheinlichkeit\: dafür,\: dass\: Luisa\: die\: Augensumme\: 15\: erhält,\: \frac{5}{54}\: beträgt
$
$\qquad\:\:$ Für $3$ Würfen, es gibt $2$ mögliche Kombinationen um die Augensumme $15$ zu haben
$\qquad\qquad$ $ \begin{cases} Kombination\: 1:\: 5-5-5\\ \\ Kombination\: 2:\: 4-5-6\: (in\: beliebiger\: Reihenfolge) \begin{cases} 4-5-6\\ 4-6-5\\ 5-4-6\\ 5-6-4\\ 6-5-4\\ 6-4-5 \end{cases}\:\:\:\: 6\: Möglichkeiten \end{cases} $
$\qquad\qquad$ Kombination 1: $ P(5-5-5)= \Large \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} = \frac{1}{27} = \frac{2}{54} $
$\qquad\qquad$ Kombination 2: $ 6 \cdot P(4-5-6)= 6 \cdot \Large \frac{1}{6} \cdot \frac{1}{3} \cdot \frac{1}{6} = \frac{1}{18} = \frac{3}{54} $
$\qquad\:\:$ Kombination 1 $+$ Kombination 2 $= \Large \frac{2}{54} + \frac{3}{54} = \frac{5}{54} $
$\qquad\qquad$ $ \underline { \Large P_{(Die\: Augensumme\: ist\: 15)}= \frac{5}{54} } $
$\qquad\:\:$ Für $3$ Würfen, es gibt $2$ mögliche Kombinationen um die Augensumme $15$ zu haben
$\qquad\qquad$ $ \begin{cases} Kombination\: 1:\: 5-5-5\\ \\ Kombination\: 2:\: 4-5-6\: (in\: beliebiger\: Reihenfolge) \begin{cases} 4-5-6\\ 4-6-5\\ 5-4-6\\ 5-6-4\\ 6-5-4\\ 6-4-5 \end{cases}\:\:\:\: 6\: Möglichkeiten \end{cases} $
$\qquad\qquad$ Kombination 1: $ P(5-5-5)= \Large \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} = \frac{1}{27} = \frac{2}{54} $
$\qquad\qquad$ Kombination 2: $ 6 \cdot P(4-5-6)= 6 \cdot \Large \frac{1}{6} \cdot \frac{1}{3} \cdot \frac{1}{6} = \frac{1}{18} = \frac{3}{54} $
$\qquad\:\:$ Kombination 1 $+$ Kombination 2 $= \Large \frac{2}{54} + \frac{3}{54} = \frac{5}{54} $
$\qquad\qquad$ $ \underline { \Large P_{(Die\: Augensumme\: ist\: 15)}= \frac{5}{54} } $
Lösung f)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
f)\: Begründe,\: dass\: Pedros: Behauptung\: falsch\: ist
$
$\qquad\:\:$ Die Wahrscheinlichkeit, die Augensumme $4-5-6$ (in beliebiger Reihenfolge) zu würfeln,
$\qquad\:\:$ ist für beide Würfel gleich.
$\qquad\:\:$ Für den $5er-$Würfel ist die Wahrscheinlichkeit, $5-5-5$ zu würfeln, wesentlich
$\qquad\:\:$ größer als für den $6er-$Würfel. Daher ist Pedros Behauptung falsch.
$\qquad\:\:$ Die Wahrscheinlichkeit, die Augensumme $4-5-6$ (in beliebiger Reihenfolge) zu würfeln,
$\qquad\:\:$ ist für beide Würfel gleich.
$\qquad\:\:$ Für den $5er-$Würfel ist die Wahrscheinlichkeit, $5-5-5$ zu würfeln, wesentlich
$\qquad\:\:$ größer als für den $6er-$Würfel. Daher ist Pedros Behauptung falsch.
Zentralabitur 2020 - Mathe Grundkurs - Teil 2 - Theater
Zentralabitur 2020 – Mathe Grundkurs – Teil 2 – Theater
Aufgabe 3.2: Theater

Lösung a)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
a)\: Koordinaten\: der\: Punkte\: H\: und\: G
$
$\qquad\:\:$ $ H \begin{pmatrix} 0\\10\\6 \end{pmatrix} $ und $ G \begin{pmatrix} 10\\10\\6 \end{pmatrix} $
$\qquad\:\:$ Berechne die Länge $|\overline{EL}|$ und $|\overline{EK}|$ und vergleich.
$\qquad\qquad$ $ |\overline{EL}|=\sqrt{(10-0)^2+(0-0)^2+(4-6)^2}=\sqrt{104}\approx10,2 $
$\qquad\qquad$ $ |\overline{EK}|=\sqrt{(2-0)^2+(10-0)^2+(0-0)^2}=\sqrt{104}\approx10,2 $
$\qquad\qquad$ $ |\overline{EL}|=|\overline{EK}| \Longrightarrow das\: Dreieck \: $ELK$\: ist \: gleichschenklig. $
$\qquad\:\:$ $ H \begin{pmatrix} 0\\10\\6 \end{pmatrix} $ und $ G \begin{pmatrix} 10\\10\\6 \end{pmatrix} $
$\qquad\:\:$ Berechne die Länge $|\overline{EL}|$ und $|\overline{EK}|$ und vergleich.
$\qquad\qquad$ $ |\overline{EL}|=\sqrt{(10-0)^2+(0-0)^2+(4-6)^2}=\sqrt{104}\approx10,2 $
$\qquad\qquad$ $ |\overline{EK}|=\sqrt{(2-0)^2+(10-0)^2+(0-0)^2}=\sqrt{104}\approx10,2 $
$\qquad\qquad$ $ |\overline{EL}|=|\overline{EK}| \Longrightarrow das\: Dreieck \: $ELK$\: ist \: gleichschenklig. $
Lösung b)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
b)\: Gleichung\: der\: Ebene\: E_p\: in\: Parameter-\: und\: in\: Koordinatenform
$
$\qquad\:\:$ $E_p$ in Parameterform:
$\qquad\qquad$ $ E_p: \vec{x}= \begin{pmatrix} 0\\0\\6 \end{pmatrix} + r\cdot \begin{pmatrix} 10-0\\0-0\\4-6 \end{pmatrix} + s\cdot \begin{pmatrix} 2-0\\10-0\\6-6 \end{pmatrix} $
$\qquad\qquad\qquad\:\:\:\:$ $ = \begin{pmatrix} 0\\0\\6 \end{pmatrix} + r\cdot \begin{pmatrix} 10\\0\\-2 \end{pmatrix} + s\cdot \begin{pmatrix} 2\\10\\0 \end{pmatrix} $
$\qquad\:\:$ $E_p$ in Koordinatenform:
$\qquad\:\:$ Kreuzprodukt von beiden Richtungsvektoren (Normalenvektor $\vec{n}$)
$\qquad\qquad$ $ \vec{n} = \begin{pmatrix} 10\\0\\-2 \end{pmatrix} \times \begin{pmatrix} 2\\10\\0 \end{pmatrix} = \begin{pmatrix} 0\cdot 0-10\cdot (-2)\\ -2\cdot 2-10\cdot 0\\ 10\cdot10-0\cdot2 \end{pmatrix} = \begin{pmatrix} 20\\-4\\100 \end{pmatrix} $
$\qquad\:\:$ Berechne $d=\vec{a}\cdot\vec{n}$, Punktprodukt Normalen- und Ortsvektor
$\qquad\qquad$ $ d= \begin{pmatrix} 0\\0\\6 \end{pmatrix} \cdot \begin{pmatrix} 20\\-4\\100 \end{pmatrix} = 0\cdot20+0\cdot(-4)+6\cdot100=600 $
$\qquad\qquad$ Also $ E_p:20x-4y+100z \:\: \textcolor{red}{|:4} $
$\qquad\qquad$ $\iff \underline{ E_p:5x-y+25z } $
$\qquad\:\:$ $E_p$ in Parameterform:
$\qquad\qquad$ $ E_p: \vec{x}= \begin{pmatrix} 0\\0\\6 \end{pmatrix} + r\cdot \begin{pmatrix} 10-0\\0-0\\4-6 \end{pmatrix} + s\cdot \begin{pmatrix} 2-0\\10-0\\6-6 \end{pmatrix} $
$\qquad\qquad\qquad\:\:\:\:$ $ = \begin{pmatrix} 0\\0\\6 \end{pmatrix} + r\cdot \begin{pmatrix} 10\\0\\-2 \end{pmatrix} + s\cdot \begin{pmatrix} 2\\10\\0 \end{pmatrix} $
$\qquad\:\:$ $E_p$ in Koordinatenform:
$\qquad\:\:$ Kreuzprodukt von beiden Richtungsvektoren (Normalenvektor $\vec{n}$)
$\qquad\qquad$ $ \vec{n} = \begin{pmatrix} 10\\0\\-2 \end{pmatrix} \times \begin{pmatrix} 2\\10\\0 \end{pmatrix} = \begin{pmatrix} 0\cdot 0-10\cdot (-2)\\ -2\cdot 2-10\cdot 0\\ 10\cdot10-0\cdot2 \end{pmatrix} = \begin{pmatrix} 20\\-4\\100 \end{pmatrix} $
$\qquad\:\:$ Berechne $d=\vec{a}\cdot\vec{n}$, Punktprodukt Normalen- und Ortsvektor
$\qquad\qquad$ $ d= \begin{pmatrix} 0\\0\\6 \end{pmatrix} \cdot \begin{pmatrix} 20\\-4\\100 \end{pmatrix} = 0\cdot20+0\cdot(-4)+6\cdot100=600 $
$\qquad\qquad$ Also $ E_p:20x-4y+100z \:\: \textcolor{red}{|:4} $
$\qquad\qquad$ $\iff \underline{ E_p:5x-y+25z } $
Lösung c)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
c)\:Begründe\: dass\: E_B:5x-y+25z=50
$
$\qquad\:\:$ Der Boden des Zuschauerraums ist parallel zur Plane
$\qquad\qquad$ $ \Longrightarrow $ der Boden liegt in der Ebene $E_B:5x-y+25=d$
$\qquad\qquad\qquad$ und durch Einsetzen der Koordinaten von $B$, ist $\underline{E_B:5x-y+25=50}$
$\qquad\:\:$ Die größte Höhe des Bodens über der Grundfläche wird an dem Eckpunkt de s Bodens angenommen,
$\qquad\:\:$ der auf der Kante DH liegt.
$\qquad\qquad$ $ \Longrightarrow \begin{cases} x=0\\ \\ und\\ \\ y=10 \end{cases} $, also $5\cdot0-10+25z=50 \Rightarrow$ z=2,4.
$\qquad\:\:$ Die größte Höhe des Bodens über der Grundfläche beträgt: $\underline{h=2,4m}$
$\qquad\:\:$ Der Boden des Zuschauerraums ist parallel zur Plane
$\qquad\qquad$ $ \Longrightarrow $ der Boden liegt in der Ebene $E_B:5x-y+25=d$
$\qquad\qquad\qquad$ und durch Einsetzen der Koordinaten von $B$, ist $\underline{E_B:5x-y+25=50}$
$\qquad\:\:$ Die größte Höhe des Bodens über der Grundfläche wird an dem Eckpunkt de s Bodens angenommen,
$\qquad\:\:$ der auf der Kante DH liegt.
$\qquad\qquad$ $ \Longrightarrow \begin{cases} x=0\\ \\ und\\ \\ y=10 \end{cases} $, also $5\cdot0-10+25z=50 \Rightarrow$ z=2,4.
$\qquad\:\:$ Die größte Höhe des Bodens über der Grundfläche beträgt: $\underline{h=2,4m}$
Lösung d)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
d)\:Begründe\: dass\: der\: Abstand\: der\: Plane\: vom\: Boden\: des\: Zuschauerraums\:<4m
$
$\qquad\:\:$ Der Punkt $L$ der Plane ist $4m$ entfernt von Punkt $B$ des Bodens.
$\qquad\:\:$ Die Strecke $|\overline{LB}|$ verläuft nicht senkrecht zu den beiden Ebenen
$\qquad\qquad$ $ \iff |\overline{LB}|$ ist länger als der Abstand der beiden Ebenen.
$\qquad\:\:$ Der Punkt $L$ der Plane ist $4m$ entfernt von Punkt $B$ des Bodens.
$\qquad\:\:$ Die Strecke $|\overline{LB}|$ verläuft nicht senkrecht zu den beiden Ebenen
$\qquad\qquad$ $ \iff |\overline{LB}|$ ist länger als der Abstand der beiden Ebenen.
Lösung e)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
e)\:Berechne\: die\: Größe\: der\:trapezförmigen\: Bühnenfläche
$
$\qquad\:\:$ Schnittgerade $S_G$ von $E_B$ und die Bühnenebene
$\qquad\qquad$ $E_B=5x-y+25z=50$ und $ S_G= \begin{pmatrix} x\\ y\\ 0,8 \end{pmatrix} $
$\qquad\qquad$ Mit $x=r$, $5r-y+20=50 \Longrightarrow y=-30+5r$
$\qquad\qquad$ $ \iff S_G:\vec{x}= \begin{pmatrix} 0\\-30\\0,8 \end{pmatrix} +r \cdot \begin{pmatrix} 1\\5\\0 \end{pmatrix} $
$\qquad\:\:$ Bestimme die $x-Werte$ der Schnittpunkt der Geraden $S_G$ mit den Seitenflächen
$\qquad\:\:$ $ABFE$ und $DCGH$
$\qquad \qquad $ Für den Schnittpunkt $S_{ABFE}$ gilt: $y=0 \Rightarrow 0=-30+5r \longrightarrow \begin{cases} r=6\\ also\\ x=6 \end{cases} $
$\qquad \qquad $ Für den Schnittpunkt $S_{DCGH}$ gilt: $y=10 \Rightarrow 10=-30+5r \longrightarrow \begin{cases} r=8\\ also\\ x=8 \end{cases} $
$\qquad \qquad $ Also bekommst du die parallelen Trapezseiten Länge: $ \begin{cases} c=10-6=4\: LE\\ und\\ a=10-8=2\: LE \end{cases} $
$\qquad\:\:$ Für ein Trapez gilt $A=\frac{a+c}{2}\cdot h$ mit $ \begin{cases} a=2\: LE\\ \\ c=4\: LE\\ \\ h=10\: LE \end{cases} $
$\qquad \qquad $ Also: $A=\frac{2+4}{2}\cdot 10=30$, die Bühne hat eine Fläche von $\underline{A=30 m^2}$
$\qquad\:\:$ Schnittgerade $S_G$ von $E_B$ und die Bühnenebene
$\qquad\qquad$ $E_B=5x-y+25z=50$ und $ S_G= \begin{pmatrix} x\\ y\\ 0,8 \end{pmatrix} $
$\qquad\qquad$ Mit $x=r$, $5r-y+20=50 \Longrightarrow y=-30+5r$
$\qquad\qquad$ $ \iff S_G:\vec{x}= \begin{pmatrix} 0\\-30\\0,8 \end{pmatrix} +r \cdot \begin{pmatrix} 1\\5\\0 \end{pmatrix} $
$\qquad\:\:$ Bestimme die $x-Werte$ der Schnittpunkt der Geraden $S_G$ mit den Seitenflächen
$\qquad\:\:$ $ABFE$ und $DCGH$
$\qquad \qquad $ Für den Schnittpunkt $S_{ABFE}$ gilt: $y=0 \Rightarrow 0=-30+5r \longrightarrow \begin{cases} r=6\\ also\\ x=6 \end{cases} $
$\qquad \qquad $ Für den Schnittpunkt $S_{DCGH}$ gilt: $y=10 \Rightarrow 10=-30+5r \longrightarrow \begin{cases} r=8\\ also\\ x=8 \end{cases} $
$\qquad \qquad $ Also bekommst du die parallelen Trapezseiten Länge: $ \begin{cases} c=10-6=4\: LE\\ und\\ a=10-8=2\: LE \end{cases} $
$\qquad\:\:$ Für ein Trapez gilt $A=\frac{a+c}{2}\cdot h$ mit $ \begin{cases} a=2\: LE\\ \\ c=4\: LE\\ \\ h=10\: LE \end{cases} $
$\qquad \qquad $ Also: $A=\frac{2+4}{2}\cdot 10=30$, die Bühne hat eine Fläche von $\underline{A=30 m^2}$
Zentralabitur 2020 - Mathe Grundkurs - Teil 2 - Teststrecke
Zentralabitur 2020 – Mathe Grundkurs – Teil 2 – Teststrecke
Aufgabe 3.1: Ebenen

Lösung a)
Gegeben sind die Ebene:
$ E_1:\vec{x} = \begin{pmatrix} 3\\ 0\\ 0 \end{pmatrix} +r\cdot \begin{pmatrix} -3\\ 9\\ 0 \end{pmatrix} +s\cdot \begin{pmatrix} 3\\ 0\\ -4 \end{pmatrix}, $ in parameterform
und
$ E_2:6x+2y+9z=18, $ in Koordinatenform.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize a)\: Bestimme\: für\: E_1\: eine\: Ebenengleichung\: in \: Koordinatenform $
$\qquad\:\:$ $ E_1:\vec{x} = \begin{pmatrix} 3\\ 0\\ 0 \end{pmatrix} +r\cdot \begin{pmatrix} -3\\ 9\\ 0 \end{pmatrix} +s\cdot \begin{pmatrix} 3\\ 0\\ -4 \end{pmatrix} $
$\qquad\qquad$ Normalenvektor $\vec{n}$ der beiden Richtungsvektoren
$\qquad\qquad$ Mit Kreuzprodukt:
$\qquad\qquad$ $ \vec{n}= \begin{pmatrix} -3\\ 9\\ 0 \end{pmatrix} \times \begin{pmatrix} 3\\ 0\\ -4 \end{pmatrix} = \begin{pmatrix} 9\cdot (-4)-0\cdot 0\\ 0\cdot 3-(-3)\cdot (-4)\\ -3\cdot 0-9\cdot 3 \end{pmatrix} = \underline{ \begin{pmatrix} -36\\ -12\\ -27 \end{pmatrix} } $
$\qquad\qquad$ Berechne $d$ (Skalarprodukt aus Ortsvektor und Normalenvektor)
$\qquad\qquad$ $ d=\vec{o}\cdot \vec{n} = \begin{pmatrix} 3\\ 0\\ 0 \end{pmatrix} \cdot \begin{pmatrix} -36\\ -12\\ -27 \end{pmatrix} =3\cdot (-36)+0\cdot (-12)+0\cdot (-27)=-108 $
$\qquad\qquad$ $ \longrightarrow d=-108 $
$\qquad\qquad\qquad$ Also: $E_1:-36x-12y-27z=-108\:\: \textcolor{red}{|:(-3)}$
$\qquad\qquad\qquad$ Die Ebenengleichung lautet: $\underline{E_1:12x+4y+9z=36}$
$ E_1:\vec{x} = \begin{pmatrix} 3\\ 0\\ 0 \end{pmatrix} +r\cdot \begin{pmatrix} -3\\ 9\\ 0 \end{pmatrix} +s\cdot \begin{pmatrix} 3\\ 0\\ -4 \end{pmatrix}, $ in parameterform
und
$ E_2:6x+2y+9z=18, $ in Koordinatenform.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize a)\: Bestimme\: für\: E_1\: eine\: Ebenengleichung\: in \: Koordinatenform $
$\qquad\:\:$ $ E_1:\vec{x} = \begin{pmatrix} 3\\ 0\\ 0 \end{pmatrix} +r\cdot \begin{pmatrix} -3\\ 9\\ 0 \end{pmatrix} +s\cdot \begin{pmatrix} 3\\ 0\\ -4 \end{pmatrix} $
$\qquad\qquad$ Normalenvektor $\vec{n}$ der beiden Richtungsvektoren
$\qquad\qquad$ Mit Kreuzprodukt:
$\qquad\qquad$ $ \vec{n}= \begin{pmatrix} -3\\ 9\\ 0 \end{pmatrix} \times \begin{pmatrix} 3\\ 0\\ -4 \end{pmatrix} = \begin{pmatrix} 9\cdot (-4)-0\cdot 0\\ 0\cdot 3-(-3)\cdot (-4)\\ -3\cdot 0-9\cdot 3 \end{pmatrix} = \underline{ \begin{pmatrix} -36\\ -12\\ -27 \end{pmatrix} } $
$\qquad\qquad$ Berechne $d$ (Skalarprodukt aus Ortsvektor und Normalenvektor)
$\qquad\qquad$ $ d=\vec{o}\cdot \vec{n} = \begin{pmatrix} 3\\ 0\\ 0 \end{pmatrix} \cdot \begin{pmatrix} -36\\ -12\\ -27 \end{pmatrix} =3\cdot (-36)+0\cdot (-12)+0\cdot (-27)=-108 $
$\qquad\qquad$ $ \longrightarrow d=-108 $
$\qquad\qquad\qquad$ Also: $E_1:-36x-12y-27z=-108\:\: \textcolor{red}{|:(-3)}$
$\qquad\qquad\qquad$ Die Ebenengleichung lautet: $\underline{E_1:12x+4y+9z=36}$
Lösung b)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
b)\: Die\: 3\: Schnittpunkte\: der\: Ebene\: E_1\: mit\: den\: Koordinateachsen
$
$\qquad\:\:$ Für die $x-Achse$ gilt: $y=z=0$
$\qquad\qquad$ $ 12x+4(0)+9(0)=36\:\: \textcolor{red}{|:12} $
$\qquad\qquad\qquad\qquad\qquad\:\:\:\:$ $ x=3 \longrightarrow \underline{S_x(3|0|0)} $
$\qquad\:\:$ Für die $y-Achse$ gilt: $x=z=0$
$\qquad\qquad$ $ 12(0)+4y+9(0)=36\:\: \textcolor{red}{|:4} $
$\qquad\qquad\qquad\qquad\qquad\:\:\:\:$ $ y=9 \longrightarrow \underline{S_y(0|9|0)} $
$\qquad\:\:$ Für die $z-Achse$ gilt: $x=y=0$
$\qquad\qquad$ $ 12(0)+4(0)+9z=36\:\: \textcolor{red}{|:9} $
$\qquad\qquad\qquad\qquad\qquad\:\:\:\:$ $ z=4 \longrightarrow \underline{S_y(0|0|4)} $
$\qquad\:\:$ Für die $x-Achse$ gilt: $y=z=0$
$\qquad\qquad$ $ 12x+4(0)+9(0)=36\:\: \textcolor{red}{|:12} $
$\qquad\qquad\qquad\qquad\qquad\:\:\:\:$ $ x=3 \longrightarrow \underline{S_x(3|0|0)} $
$\qquad\:\:$ Für die $y-Achse$ gilt: $x=z=0$
$\qquad\qquad$ $ 12(0)+4y+9(0)=36\:\: \textcolor{red}{|:4} $
$\qquad\qquad\qquad\qquad\qquad\:\:\:\:$ $ y=9 \longrightarrow \underline{S_y(0|9|0)} $
$\qquad\:\:$ Für die $z-Achse$ gilt: $x=y=0$
$\qquad\qquad$ $ 12(0)+4(0)+9z=36\:\: \textcolor{red}{|:9} $
$\qquad\qquad\qquad\qquad\qquad\:\:\:\:$ $ z=4 \longrightarrow \underline{S_y(0|0|4)} $
Lösung c)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
c)\: Abstand\: der\: Ebene\: E_1\: zum\: Koordinatenursprung\: 0
$
$\qquad\:\:$ $ d(E_1,O)= \begin{vmatrix} \frac { \begin{pmatrix} 12\\4\\9 \end{pmatrix} \cdot \begin{pmatrix} 0\\0\\0 \end{pmatrix} -36 } { \begin{vmatrix} \begin{pmatrix} 12\\4\\9 \end{pmatrix} \end{vmatrix} \cdot \begin{vmatrix} \begin{pmatrix} 0\\0\\0 \end{pmatrix} \end{vmatrix} } \end{vmatrix} = \begin{vmatrix} \frac { 12\cdot 0+4\cdot 0+9\cdot 0-36 } { \sqrt{12^2+4^2+9^2} } \end{vmatrix} =2,318 $
$\qquad\:\:$ Der Abstand beträgt $\underline{d\approx2,32\: LE}$
$\qquad\:\:$ $ d(E_1,O)= \begin{vmatrix} \frac { \begin{pmatrix} 12\\4\\9 \end{pmatrix} \cdot \begin{pmatrix} 0\\0\\0 \end{pmatrix} -36 } { \begin{vmatrix} \begin{pmatrix} 12\\4\\9 \end{pmatrix} \end{vmatrix} \cdot \begin{vmatrix} \begin{pmatrix} 0\\0\\0 \end{pmatrix} \end{vmatrix} } \end{vmatrix} = \begin{vmatrix} \frac { 12\cdot 0+4\cdot 0+9\cdot 0-36 } { \sqrt{12^2+4^2+9^2} } \end{vmatrix} =2,318 $
$\qquad\:\:$ Der Abstand beträgt $\underline{d\approx2,32\: LE}$
Lösung d)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
d)\: Begründe,\: dass\: E_1\: und\: E_2\: nicht\: zueinander \: parallel\: sind
$
$\qquad\:\:$ $E_1: 12x+4y+9z=36 \longrightarrow$ der Normalenvektor $ n_1 = \begin{pmatrix} 12\\4\\9 \end{pmatrix} $
$\qquad\:\:$ $E_2: 6x+2y+9z=18 \longrightarrow$ der Normalenvektor $ n_2 = \begin{pmatrix} 6\\2\\9 \end{pmatrix} $
$\qquad\:\:$ $ \begin{pmatrix} 12\\4\\9 \end{pmatrix} \ne r\cdot \begin{pmatrix} 6\\2\\9 \end{pmatrix} \longrightarrow $ $E_1$ und $E_2$ sind nicht kollinear und dann nicht parallel.
$\qquad\:\:$ Schnittgerade der Ebenen $E_1$ und $E_2$
$\qquad\qquad$ $ E_1 \cap E_2: 6(3-3r+3s)+2(9r)+9(-4s)=18 $
$\qquad\qquad\qquad\:\:\:$ $ \iff \textcolor{red}{\cancel{18}} \textcolor{blue}{\cancel{-18r}} \underline{+ 18s} \textcolor{blue}{\cancel{+18r}} \underline{- 36s}=\textcolor{red}{\cancel{18}} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:$ $ \iff -18s=0 \longrightarrow \underline{s=0} $
$\qquad\qquad$ Setzte $s=0$ in $E_1$ ein
$\qquad\qquad$ $ \iff \begin{pmatrix} 3\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -3\\9\\0 \end{pmatrix} + 0\cdot \begin{pmatrix} 3\\0\\-4 \end{pmatrix} = \begin{pmatrix} 3\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -3\\9\\0 \end{pmatrix} $
$\qquad\:\:$ Die Gleichung der Schnittgerade $s$ lautet:
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad$ $ \underline { s:\vec{x} = \begin{pmatrix} 3\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -3\\9\\0 \end{pmatrix} } $
$\qquad\:\:$ $E_1: 12x+4y+9z=36 \longrightarrow$ der Normalenvektor $ n_1 = \begin{pmatrix} 12\\4\\9 \end{pmatrix} $
$\qquad\:\:$ $E_2: 6x+2y+9z=18 \longrightarrow$ der Normalenvektor $ n_2 = \begin{pmatrix} 6\\2\\9 \end{pmatrix} $
$\qquad\:\:$ $ \begin{pmatrix} 12\\4\\9 \end{pmatrix} \ne r\cdot \begin{pmatrix} 6\\2\\9 \end{pmatrix} \longrightarrow $ $E_1$ und $E_2$ sind nicht kollinear und dann nicht parallel.
$\qquad\:\:$ Schnittgerade der Ebenen $E_1$ und $E_2$
$\qquad\qquad$ $ E_1 \cap E_2: 6(3-3r+3s)+2(9r)+9(-4s)=18 $
$\qquad\qquad\qquad\:\:\:$ $ \iff \textcolor{red}{\cancel{18}} \textcolor{blue}{\cancel{-18r}} \underline{+ 18s} \textcolor{blue}{\cancel{+18r}} \underline{- 36s}=\textcolor{red}{\cancel{18}} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:$ $ \iff -18s=0 \longrightarrow \underline{s=0} $
$\qquad\qquad$ Setzte $s=0$ in $E_1$ ein
$\qquad\qquad$ $ \iff \begin{pmatrix} 3\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -3\\9\\0 \end{pmatrix} + 0\cdot \begin{pmatrix} 3\\0\\-4 \end{pmatrix} = \begin{pmatrix} 3\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -3\\9\\0 \end{pmatrix} $
$\qquad\:\:$ Die Gleichung der Schnittgerade $s$ lautet:
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad$ $ \underline { s:\vec{x} = \begin{pmatrix} 3\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -3\\9\\0 \end{pmatrix} } $
Lösung e)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
e)\: dass\: Volumen\: der\: Pyramide
$
$\qquad\:\:$ $ \underline { V_{Pyramide}= \frac{1}{3}A_G \cdot h=\frac{1}{3}(\frac{1}{2} \cdot 3\cdot 9)\cdot 4=18\: VE } $
$\qquad\:\:$ $ \underline { V_{Pyramide}= \frac{1}{3}A_G \cdot h=\frac{1}{3}(\frac{1}{2} \cdot 3\cdot 9)\cdot 4=18\: VE } $
Lösung f)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
f)\: Ermittle\: den\: Punkt\: P
$
$\qquad\:\:$ Gleichung der Geraden gAB:
$\qquad\qquad$ gAB: $ \vec{x} = \begin{pmatrix} 3\\0\\0 \end{pmatrix} +r \begin{pmatrix} 0-3\\9-0\\0-0 \end{pmatrix} = \begin{pmatrix} 3\\0\\0 \end{pmatrix} +r \begin{pmatrix} -3\\9\\0 \end{pmatrix} $
$\qquad\qquad$ $P$ auf gAB ist also $C$ auf gAB $ \longrightarrow \overrightarrow{PC}= $ gAB
$\qquad\qquad$ $ \iff \overrightarrow{PC} = \begin{pmatrix} 3\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -3\\9\\0 \end{pmatrix} – \begin{pmatrix} 0\\0\\4 \end{pmatrix} = \begin{pmatrix} 3-3r\\9r\\-4 \end{pmatrix} $
$\qquad\:\:$ $\overrightarrow{PC}\perp g_{AB} \Longrightarrow \overrightarrow{PC}\cdot g_{AB}=0$ (also Richtungsvektor von $g_{AB}$)
$\qquad\qquad$ $ \iff \begin{pmatrix} 3-3r\\9r\\-4 \end{pmatrix} \cdot \begin{pmatrix} -3\\9\\0 \end{pmatrix} = (-9+9r)+(81r)+(0)=-9+90r=0 \Rightarrow r=\frac{1}{10} $
$\qquad\:\:$ Also
$\qquad\qquad\qquad\qquad$ $ \underline { P \begin{pmatrix} 3&+&\frac{1}{10}\cdot (-3) \\ 0&+&\frac{1}{10}\cdot 9 \\ 0&+&\frac{1}{10}\cdot 0 \end{pmatrix} = \begin{pmatrix} 2,7\\0,9\\0 \end{pmatrix} } $
$\qquad\:\:$ Gleichung der Geraden gAB:
$\qquad\qquad$ gAB: $ \vec{x} = \begin{pmatrix} 3\\0\\0 \end{pmatrix} +r \begin{pmatrix} 0-3\\9-0\\0-0 \end{pmatrix} = \begin{pmatrix} 3\\0\\0 \end{pmatrix} +r \begin{pmatrix} -3\\9\\0 \end{pmatrix} $
$\qquad\qquad$ $P$ auf gAB ist also $C$ auf gAB $ \longrightarrow \overrightarrow{PC}= $ gAB
$\qquad\qquad$ $ \iff \overrightarrow{PC} = \begin{pmatrix} 3\\0\\0 \end{pmatrix} + r\cdot \begin{pmatrix} -3\\9\\0 \end{pmatrix} – \begin{pmatrix} 0\\0\\4 \end{pmatrix} = \begin{pmatrix} 3-3r\\9r\\-4 \end{pmatrix} $
$\qquad\:\:$ $\overrightarrow{PC}\perp g_{AB} \Longrightarrow \overrightarrow{PC}\cdot g_{AB}=0$ (also Richtungsvektor von $g_{AB}$)
$\qquad\qquad$ $ \iff \begin{pmatrix} 3-3r\\9r\\-4 \end{pmatrix} \cdot \begin{pmatrix} -3\\9\\0 \end{pmatrix} = (-9+9r)+(81r)+(0)=-9+90r=0 \Rightarrow r=\frac{1}{10} $
$\qquad\:\:$ Also
$\qquad\qquad\qquad\qquad$ $ \underline { P \begin{pmatrix} 3&+&\frac{1}{10}\cdot (-3) \\ 0&+&\frac{1}{10}\cdot 9 \\ 0&+&\frac{1}{10}\cdot 0 \end{pmatrix} = \begin{pmatrix} 2,7\\0,9\\0 \end{pmatrix} } $
Zentralabitur 2020 - Mathe Grundkurs - Teil 2
Zentralabitur 2020 – Mathe Grundkurs – Teil2
Aufgabe 2.2 Teststrecke


Lösung a)
$
f(x)=-0,01\cdot (x-8)(x+1)^2\: ;\:\: x\in \mathbb{R}.
$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize a)\: Gebe\: die\: Nullstellen\: von\: f\: an $
$\qquad\:\:$ $ f(x)=-0,01\cdot (x-8)(x+1)^2=0 $
$\qquad\qquad$ $ \iff \begin{cases} (x-8)=0\:\: \longrightarrow x=8\\ \\ (x+1)^2=0\:\: \textcolor{red}{|\sqrt(…)\:und\: (-1)}\:\: \longrightarrow x=-1 \end{cases} $
$\qquad\:\:$ Es gibt Nullstellen bei $\underline{x=8}$ und $\underline{x=-1}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize a)\: Gebe\: die\: Nullstellen\: von\: f\: an $
$\qquad\:\:$ $ f(x)=-0,01\cdot (x-8)(x+1)^2=0 $
$\qquad\qquad$ $ \iff \begin{cases} (x-8)=0\:\: \longrightarrow x=8\\ \\ (x+1)^2=0\:\: \textcolor{red}{|\sqrt(…)\:und\: (-1)}\:\: \longrightarrow x=-1 \end{cases} $
$\qquad\:\:$ Es gibt Nullstellen bei $\underline{x=8}$ und $\underline{x=-1}$
Lösung b)
$
f(x)=-0,01\cdot (x-8)(x+1)^2\: ;\:\: x\in \mathbb{R}.
$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b) $
$\qquad\:\:$ Zeige, dass $f$ auch in der Form $f(x)=- \frac{1}{100}x^3+ \frac{3}{50}x^2+ \frac{3}{20}x+ \frac{2}{25}$
$\qquad\:\:$ geschrieben werden kann.
$\qquad\qquad$ $ f(x)=-0,01\cdot (x-8)(x+1)^2=-0,01\cdot (x-8)(x^2+2x+1) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ =-0,01\cdot (x^3+2x^2+x-8x^2-16x-8)\:\: \textcolor{red}{| \:\cdot 100} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ =\underline{- \frac{1}{100}x^3+ \frac{3}{50}x^2+ \frac{3}{20}x+ \frac{2}{25}} $
$\qquad\:\:$ Gebe das Verhalten der Funktionswerte von $f$ für $x\to +\infty$ und $x\to -\infty$ an.
$\qquad\qquad$ $ \lim\limits_{x\to +\infty} f(x)=-\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to -\infty} f(x)= \infty $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b) $
$\qquad\:\:$ Zeige, dass $f$ auch in der Form $f(x)=- \frac{1}{100}x^3+ \frac{3}{50}x^2+ \frac{3}{20}x+ \frac{2}{25}$
$\qquad\:\:$ geschrieben werden kann.
$\qquad\qquad$ $ f(x)=-0,01\cdot (x-8)(x+1)^2=-0,01\cdot (x-8)(x^2+2x+1) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ =-0,01\cdot (x^3+2x^2+x-8x^2-16x-8)\:\: \textcolor{red}{| \:\cdot 100} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ =\underline{- \frac{1}{100}x^3+ \frac{3}{50}x^2+ \frac{3}{20}x+ \frac{2}{25}} $
$\qquad\:\:$ Gebe das Verhalten der Funktionswerte von $f$ für $x\to +\infty$ und $x\to -\infty$ an.
$\qquad\qquad$ $ \lim\limits_{x\to +\infty} f(x)=-\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to -\infty} f(x)= \infty $
Lösung c)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
c)\: Ermittle\: die\: Lage\: und\: Art\: der\: Extrempunkte\: des\: Graphen\: von\: f
$
$\qquad\qquad$ $ f^\prime(x)=-\frac{1}{100}\cdot 3x^2+ \frac{3}{50}\cdot 2x+ \frac{3}{20} $
$\qquad\qquad\qquad\:\:$ $ = -\frac{3}{100}\cdot x^2+ \frac{6}{50}\cdot x+ \frac{3}{20} $
$\qquad\qquad\qquad\:\:$ $ = -\frac{3}{100}\cdot x^2+ \frac{12}{100}\cdot x+ \frac{15}{100} $
$\qquad\qquad\qquad\:\:$ $ = \underline{-\frac{3}{100}(x^2-4x-5)} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=\underline{-\frac{3}{100}(2x-4)} $
$\qquad\:\:$ $ f^\prime(x)=0 \iff -\frac{3}{100}(x^2-4x-5)=0 \iff (x^2-4x-5)=0 \Longrightarrow \begin{cases} x_1=-1\\ \\ x_2=5 \end{cases} $
$\qquad\:\:$ $ f^{\prime\prime}(-1)= -\frac{3}{100}[2(-1)-4]=0,18>0 \longrightarrow Tiefpunkt $
$\qquad\qquad$ Es gibt ein Tiefpunkt bei $\underline{[-1|f(-1)]=(-1|0)}$
$\qquad\:\:$ $ f^{\prime\prime}(5)= -\frac{3}{100}[2(5)-4]=-0,18<0 \longrightarrow Hochpunkt $
$\qquad\qquad$ Es gibt ein Hochpunkt bei $\underline{[5|f(5)]=(5|1,08)}$
$\qquad\qquad$ $ f^\prime(x)=-\frac{1}{100}\cdot 3x^2+ \frac{3}{50}\cdot 2x+ \frac{3}{20} $
$\qquad\qquad\qquad\:\:$ $ = -\frac{3}{100}\cdot x^2+ \frac{6}{50}\cdot x+ \frac{3}{20} $
$\qquad\qquad\qquad\:\:$ $ = -\frac{3}{100}\cdot x^2+ \frac{12}{100}\cdot x+ \frac{15}{100} $
$\qquad\qquad\qquad\:\:$ $ = \underline{-\frac{3}{100}(x^2-4x-5)} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=\underline{-\frac{3}{100}(2x-4)} $
$\qquad\:\:$ $ f^\prime(x)=0 \iff -\frac{3}{100}(x^2-4x-5)=0 \iff (x^2-4x-5)=0 \Longrightarrow \begin{cases} x_1=-1\\ \\ x_2=5 \end{cases} $
$\qquad\:\:$ $ f^{\prime\prime}(-1)= -\frac{3}{100}[2(-1)-4]=0,18>0 \longrightarrow Tiefpunkt $
$\qquad\qquad$ Es gibt ein Tiefpunkt bei $\underline{[-1|f(-1)]=(-1|0)}$
$\qquad\:\:$ $ f^{\prime\prime}(5)= -\frac{3}{100}[2(5)-4]=-0,18<0 \longrightarrow Hochpunkt $
$\qquad\qquad$ Es gibt ein Hochpunkt bei $\underline{[5|f(5)]=(5|1,08)}$
Lösung d)

Lösung e)
Wo der Hochpunkt des Graphen von $f^\prime$ liegt. liegt ein Wendepunkt des Graphen von $f$.
An der Stelle, hat die Steigung des Graphen von $f$ eine relatives Extremum.
An der Stelle, hat die Steigung des Graphen von $f$ eine relatives Extremum.
Lösung f)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
f)\: Weise\: nach,\: dass\: die\: Tangente\: der\: Gleichung\: t(x)=-0,21x+2,24
$
$\qquad\:\:$ $ t(x)=f^\prime(x_0)(x-x_0)+f(x_0) \:\: mit \:\: \begin{cases} x_0=6\\ \\ f^\prime(6)=-\frac{3}{100}(6^2-4\cdot 6-5)=-0,21\\ \\ f(6)=-0,01\cdot (6-8)(6+1)^2=0,98 \end{cases} $
$\qquad\qquad$ $ \iff \underline{t(x)=-0,21(x-6)+0,98=-0,21x+2,24} $

$\qquad\:\:$ $ t(x)=f^\prime(x_0)(x-x_0)+f(x_0) \:\: mit \:\: \begin{cases} x_0=6\\ \\ f^\prime(6)=-\frac{3}{100}(6^2-4\cdot 6-5)=-0,21\\ \\ f(6)=-0,01\cdot (6-8)(6+1)^2=0,98 \end{cases} $
$\qquad\qquad$ $ \iff \underline{t(x)=-0,21(x-6)+0,98=-0,21x+2,24} $

Lösung g)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
g)\: Berechne\: das\: Volumen\: im\: Bereich\: 6 \leq x \leq10,27
$
$\qquad\:\:$ Ansatz
$\qquad\qquad$ $ V=A\cdot h\:\: mit \:\: \begin{cases} A= \int\limits_6^{10,67} t(x)dx- \int\limits_6^8 f(x)dx\:\: (Querschnittsfläche\: der\: Fahrbahn)\\ \\ h=5m\:\: (Breite\: der\: Fahrbahn) \end{cases} $
$\qquad\qquad$ $ A_1=\int\limits_6^{10,67} t(x)dx $
$\qquad\qquad\:\:\:\:\:\:$ $ =\int\limits_6^{10,67} (-0,21x+2,24)dx = \begin{bmatrix} -\frac{0,21}{2}x^2+2,24x \end{bmatrix} _6^{10,67}=11,94-9,66\approx2,29m^2 $
$\qquad\qquad$ $ A_2=\int\limits_6^8 f(x)dx $
$\qquad\qquad\:\:\:\:\:\:$ $ =\int\limits_6^8 (-\frac{1}{100}x^3 + \frac{3}{50}x^2 +\frac{3}{20}x + \frac{2}{25})dx $
$\qquad\qquad\:\:\:\:\:\:$ $ = \begin{bmatrix} -\frac{1}{400}x^4 + \frac{1}{50}x^3 +\frac{3}{40}x^2 + \frac{2}{25}x \end{bmatrix} _6^8\approx1,18m^2 $
$\qquad\:\:$ $ \underline{V=(A_1-A_2)\cdot h=(2,29m^2-1,18m^2)\cdot 5m=5,55m^3} $
$\qquad\:\:$ Ansatz
$\qquad\qquad$ $ V=A\cdot h\:\: mit \:\: \begin{cases} A= \int\limits_6^{10,67} t(x)dx- \int\limits_6^8 f(x)dx\:\: (Querschnittsfläche\: der\: Fahrbahn)\\ \\ h=5m\:\: (Breite\: der\: Fahrbahn) \end{cases} $
$\qquad\qquad$ $ A_1=\int\limits_6^{10,67} t(x)dx $
$\qquad\qquad\:\:\:\:\:\:$ $ =\int\limits_6^{10,67} (-0,21x+2,24)dx = \begin{bmatrix} -\frac{0,21}{2}x^2+2,24x \end{bmatrix} _6^{10,67}=11,94-9,66\approx2,29m^2 $
$\qquad\qquad$ $ A_2=\int\limits_6^8 f(x)dx $
$\qquad\qquad\:\:\:\:\:\:$ $ =\int\limits_6^8 (-\frac{1}{100}x^3 + \frac{3}{50}x^2 +\frac{3}{20}x + \frac{2}{25})dx $
$\qquad\qquad\:\:\:\:\:\:$ $ = \begin{bmatrix} -\frac{1}{400}x^4 + \frac{1}{50}x^3 +\frac{3}{40}x^2 + \frac{2}{25}x \end{bmatrix} _6^8\approx1,18m^2 $
$\qquad\:\:$ $ \underline{V=(A_1-A_2)\cdot h=(2,29m^2-1,18m^2)\cdot 5m=5,55m^3} $
Lösung h)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
h)\: Stelle\: der\: neuen\: Tangente\: t_neu
$
$\qquad\:\:$ Im Wendepunkt hat der Graph von $f$ die Steigung $f^\prime(2)=\frac{27}{100}$
$\qquad\:\:$ Damit die neue Tangente den gleichen Steigungswinkel hat, muss eine Steigung
$\qquad\:\:$ $f^\prime(2)=\frac{27}{100}$
$\qquad\:\:$ von $-\frac{27}{100}$ gelten. An der Stelle, muss also $f^\prime(2)=-\frac{27}{100}$
$\qquad\qquad$ $ \iff -\frac{3}{100}(x^2-4x-5)=-\frac{27}{100} $
$\qquad\qquad$ $ \Longrightarrow x^2-4x-14=0 \Longrightarrow \begin{cases} x_1=2-\sqrt{18} \longrightarrow x_1=-2,24\\ \\ x_2=2+\sqrt{18} \longrightarrow x_2=6,24 \end{cases} $
$\qquad\:\:$ $x_1$ erfüllt die Bedingung $x>5$ nicht, also $\underline{x_2=6,25}$ ist die gesuchte Stelle
$\qquad\:\:$ Im Wendepunkt hat der Graph von $f$ die Steigung $f^\prime(2)=\frac{27}{100}$
$\qquad\:\:$ Damit die neue Tangente den gleichen Steigungswinkel hat, muss eine Steigung
$\qquad\:\:$ $f^\prime(2)=\frac{27}{100}$
$\qquad\:\:$ von $-\frac{27}{100}$ gelten. An der Stelle, muss also $f^\prime(2)=-\frac{27}{100}$
$\qquad\qquad$ $ \iff -\frac{3}{100}(x^2-4x-5)=-\frac{27}{100} $
$\qquad\qquad$ $ \Longrightarrow x^2-4x-14=0 \Longrightarrow \begin{cases} x_1=2-\sqrt{18} \longrightarrow x_1=-2,24\\ \\ x_2=2+\sqrt{18} \longrightarrow x_2=6,24 \end{cases} $
$\qquad\:\:$ $x_1$ erfüllt die Bedingung $x>5$ nicht, also $\underline{x_2=6,25}$ ist die gesuchte Stelle
Zentralabitur 2020 - Mathe Grundkurs - Teil 1
Zentralabitur 2020 – Mathe Grundkurs – Teil 1

Lösung
$
F(x)=2x^4-x+1
$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize a)\: Gleichung\: der\: Funktion\: f $
$\qquad\:\:$ $F^\prime(x)=f(x) \iff f(x)= 2\cdot 4\cdot x^{4-1}-1=\underline{8x^3-1} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b) $
$\qquad\:\:$ * Gleichung aller Stammfunktionen von f
$\qquad\:\:$ $ F(x)=2x^4-x+1+C, $ mit $C\in \mathbb{R}$ ($C$ als Integrationskonstante)
$\qquad\:\:$ * Die zwei Stammfunktionen von f
$\qquad\:\:$ $ F_{1/2}(x)=2x^4-x+1\pm3 \iff \begin{cases} F_1(x)=2x^4-x+1-3=\underline{2x^4-x+1-2}\\ \\ F_2(x)=2x^4-x+1+3=\underline{2x^4-x+1+4} \end{cases} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize a)\: Gleichung\: der\: Funktion\: f $
$\qquad\:\:$ $F^\prime(x)=f(x) \iff f(x)= 2\cdot 4\cdot x^{4-1}-1=\underline{8x^3-1} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b) $
$\qquad\:\:$ * Gleichung aller Stammfunktionen von f
$\qquad\:\:$ $ F(x)=2x^4-x+1+C, $ mit $C\in \mathbb{R}$ ($C$ als Integrationskonstante)
$\qquad\:\:$ * Die zwei Stammfunktionen von f
$\qquad\:\:$ $ F_{1/2}(x)=2x^4-x+1\pm3 \iff \begin{cases} F_1(x)=2x^4-x+1-3=\underline{2x^4-x+1-2}\\ \\ F_2(x)=2x^4-x+1+3=\underline{2x^4-x+1+4} \end{cases} $

Lösung
Die quadratische Funktion lautet:
$\qquad\:\:$ $f(x)=ax^2+bx+c$, mit $a,\:b,\: und\: c \in \mathbb{R}$
Die quadratische Funktion verläuft durch $(0|0)$:
$\qquad\:\:$ $ \iff f(0)=0 \longrightarrow \underline{c=0} $
Die Tangente im Punkt $(2|f(2))$ hat die Gleichung $y=4x-2$:
$\qquad\:\:$ $ \iff \begin{cases} *\:\: f(2)=4a+2b &\longrightarrow 6=4a+2b\:\: (I)\\ \\ *\:\: f^\prime(2)=4 &\longrightarrow 4=4a+b\:\: (II) \end{cases} $
$\qquad\qquad$ (I) und (II) gleichzeitig lösen
$\qquad\qquad\qquad$ $ – \begin{cases} 6=4a+2b\:\: (I)\\ \\ 4=4a+b\:\: (II) \end{cases} \longrightarrow \underline{b=2},\:\: und\:\: \underline{a=\frac{1}{2}} $
Die Funktionsterm von $f$ lautet:
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad$ $ \underline{f(x)=\frac{1}{2}x^2+2x} $
$\qquad\:\:$ $f(x)=ax^2+bx+c$, mit $a,\:b,\: und\: c \in \mathbb{R}$
Die quadratische Funktion verläuft durch $(0|0)$:
$\qquad\:\:$ $ \iff f(0)=0 \longrightarrow \underline{c=0} $
Die Tangente im Punkt $(2|f(2))$ hat die Gleichung $y=4x-2$:
$\qquad\:\:$ $ \iff \begin{cases} *\:\: f(2)=4a+2b &\longrightarrow 6=4a+2b\:\: (I)\\ \\ *\:\: f^\prime(2)=4 &\longrightarrow 4=4a+b\:\: (II) \end{cases} $
$\qquad\qquad$ (I) und (II) gleichzeitig lösen
$\qquad\qquad\qquad$ $ – \begin{cases} 6=4a+2b\:\: (I)\\ \\ 4=4a+b\:\: (II) \end{cases} \longrightarrow \underline{b=2},\:\: und\:\: \underline{a=\frac{1}{2}} $
Die Funktionsterm von $f$ lautet:
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad$ $ \underline{f(x)=\frac{1}{2}x^2+2x} $

Lösung
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
a)\: Weise\: nach,\: dass\: A,\: B\: und\: C\: auf\: einer\: Geraden\: g\: liegen
$
$\qquad\:\:$ * Ermittle die Gerade $AB$
$\qquad\qquad$ $g_{AB}: \vec{x}= \begin{pmatrix} 3\\4\\-1 \end{pmatrix} + r\cdot \begin{bmatrix} \begin{pmatrix} 4\\6\\0 \end{pmatrix} – \begin{pmatrix} 3\\4\\-1 \end{pmatrix} \end{bmatrix} = \underline { \begin{pmatrix} 3\\4\\-1 \end{pmatrix} + r\cdot \begin{pmatrix} 1\\2\\1 \end{pmatrix} } $
$\qquad\:\:$ * Probe ob $C$ auf $g_{AB}$ liegt
$\qquad\qquad$ $ \iff \begin{pmatrix} 1\\0\\-3 \end{pmatrix} = \begin{pmatrix} 3\\4\\-1 \end{pmatrix} + r\cdot \begin{pmatrix} 1\\2\\1 \end{pmatrix} \iff \begin{cases} 1=3+r &\longrightarrow r=-2\\ \\ 0=4+2r &\longrightarrow r=-2\\ \\ -3=-1+r &\longrightarrow r=-2 \end{cases} $
$\qquad\:\:$ $C$ liegt auf $g_{AB}$ ist erfüllt für $r=-2$
$\qquad\qquad\qquad$ $ \Longrightarrow $ Die drei Punkte $A$, $B$ und $C$ liegen auf der Geraden $g$.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b)\: Koordinaten\: des\: weiteren\: Punktes\: D $
$\qquad\:\:$ Für $r=1$, $ \begin{pmatrix} 3\\4\\-1 \end{pmatrix} + 1\cdot \begin{pmatrix} 1\\2\\1 \end{pmatrix} = \begin{pmatrix} 4\\6\\0 \end{pmatrix} \longrightarrow $ die Geradengleichung $\overline{OB}$
$\qquad\:\:$ Für $r=-1$, $ \begin{pmatrix} 3\\4\\-1 \end{pmatrix} + (-1)\cdot \begin{pmatrix} 1\\2\\1 \end{pmatrix} = \begin{pmatrix} 2\\2\\-2 \end{pmatrix} \longrightarrow D \begin{pmatrix} 2\\2\\-2 \end{pmatrix} $, mit $ | \overrightarrow{AB} | = | \overrightarrow{AD} | $
$\qquad\:\:$ * Ermittle die Gerade $AB$
$\qquad\qquad$ $g_{AB}: \vec{x}= \begin{pmatrix} 3\\4\\-1 \end{pmatrix} + r\cdot \begin{bmatrix} \begin{pmatrix} 4\\6\\0 \end{pmatrix} – \begin{pmatrix} 3\\4\\-1 \end{pmatrix} \end{bmatrix} = \underline { \begin{pmatrix} 3\\4\\-1 \end{pmatrix} + r\cdot \begin{pmatrix} 1\\2\\1 \end{pmatrix} } $
$\qquad\:\:$ * Probe ob $C$ auf $g_{AB}$ liegt
$\qquad\qquad$ $ \iff \begin{pmatrix} 1\\0\\-3 \end{pmatrix} = \begin{pmatrix} 3\\4\\-1 \end{pmatrix} + r\cdot \begin{pmatrix} 1\\2\\1 \end{pmatrix} \iff \begin{cases} 1=3+r &\longrightarrow r=-2\\ \\ 0=4+2r &\longrightarrow r=-2\\ \\ -3=-1+r &\longrightarrow r=-2 \end{cases} $
$\qquad\:\:$ $C$ liegt auf $g_{AB}$ ist erfüllt für $r=-2$
$\qquad\qquad\qquad$ $ \Longrightarrow $ Die drei Punkte $A$, $B$ und $C$ liegen auf der Geraden $g$.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b)\: Koordinaten\: des\: weiteren\: Punktes\: D $
$\qquad\:\:$ Für $r=1$, $ \begin{pmatrix} 3\\4\\-1 \end{pmatrix} + 1\cdot \begin{pmatrix} 1\\2\\1 \end{pmatrix} = \begin{pmatrix} 4\\6\\0 \end{pmatrix} \longrightarrow $ die Geradengleichung $\overline{OB}$
$\qquad\:\:$ Für $r=-1$, $ \begin{pmatrix} 3\\4\\-1 \end{pmatrix} + (-1)\cdot \begin{pmatrix} 1\\2\\1 \end{pmatrix} = \begin{pmatrix} 2\\2\\-2 \end{pmatrix} \longrightarrow D \begin{pmatrix} 2\\2\\-2 \end{pmatrix} $, mit $ | \overrightarrow{AB} | = | \overrightarrow{AD} | $

Lösung
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
a)\: Abstand\: der\: Punkte\: A\: und\: B
$
$\qquad\:\:$ $ \overrightarrow{AB} = \overrightarrow{B} – \overrightarrow{A} = \begin{pmatrix} 4&-&7\\ 1&-&(-3)\\ 5&-&5 \end{pmatrix} = \begin{pmatrix} -3\\ 4\\ 0 \end{pmatrix} $
$\qquad\:\:$ $ |\overrightarrow{AB}| =\sqrt{(-3)^2+4^2+0^2}=\sqrt{25}=5 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b)\:Koordinaten\: der\: möglichen\: Punktes\: C $
$\qquad\:\:$ Ein gleichschenkliges Dreieck, mit Flächeninhalt von $10\:FE$
$\qquad\qquad$ $ \longrightarrow \frac{1}{2}\cdot g\cdot h=10\:FE $, $ \: g=|\overrightarrow{AB}|=5 $
$\qquad\qquad\qquad$ $ \frac{1}{2}\cdot 5\cdot h=10\:\:\: \textcolor{red}{|\cdot 2} $
$\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ 5\cdot h=20\:\:\: \textcolor{red}{|:5} $
$\qquad\qquad\qquad\qquad\:\:\:$ $ \underline{h=4\:LE} $, Höhe des Dreiecks
$\qquad\:\:$ $|AC|$ und $|BC|$ sollen gleichschenklig sein
$\qquad\qquad$ $\longrightarrow$ der Punkt $C$ liegt senkrecht über dem Mittelpunkt der Strecke $\overline{AB}$
$\qquad\qquad$ $ M ( \frac{4+7}{2}\:|\: \frac{1-3}{2}\:|\: \frac{5+5}{2} ) = (5,5\:|\: -1\:|\: 5) $
$\qquad\:\:$ Ein möglicher Punkt wäre $\underline{C(5,5\:|\: -1\:|\: 5+4)=(5,5\:|\: -1\:|\: 9)}$
$\qquad\:\:$ $ \overrightarrow{AB} = \overrightarrow{B} – \overrightarrow{A} = \begin{pmatrix} 4&-&7\\ 1&-&(-3)\\ 5&-&5 \end{pmatrix} = \begin{pmatrix} -3\\ 4\\ 0 \end{pmatrix} $
$\qquad\:\:$ $ |\overrightarrow{AB}| =\sqrt{(-3)^2+4^2+0^2}=\sqrt{25}=5 $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b)\:Koordinaten\: der\: möglichen\: Punktes\: C $
$\qquad\:\:$ Ein gleichschenkliges Dreieck, mit Flächeninhalt von $10\:FE$
$\qquad\qquad$ $ \longrightarrow \frac{1}{2}\cdot g\cdot h=10\:FE $, $ \: g=|\overrightarrow{AB}|=5 $
$\qquad\qquad\qquad$ $ \frac{1}{2}\cdot 5\cdot h=10\:\:\: \textcolor{red}{|\cdot 2} $
$\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ 5\cdot h=20\:\:\: \textcolor{red}{|:5} $
$\qquad\qquad\qquad\qquad\:\:\:$ $ \underline{h=4\:LE} $, Höhe des Dreiecks
$\qquad\:\:$ $|AC|$ und $|BC|$ sollen gleichschenklig sein
$\qquad\qquad$ $\longrightarrow$ der Punkt $C$ liegt senkrecht über dem Mittelpunkt der Strecke $\overline{AB}$
$\qquad\qquad$ $ M ( \frac{4+7}{2}\:|\: \frac{1-3}{2}\:|\: \frac{5+5}{2} ) = (5,5\:|\: -1\:|\: 5) $
$\qquad\:\:$ Ein möglicher Punkt wäre $\underline{C(5,5\:|\: -1\:|\: 5+4)=(5,5\:|\: -1\:|\: 9)}$

Lösung
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
a)\: Wahrscheinlichkeit\: beiden\: Kugeln\: unterschiedliche\: Farben\: haben
$
$\qquad\:\:$ $ P_{untersch. Farben}(B/R) = \frac{3}{5} \cdot \frac{2}{4} + \frac{2}{5} \cdot \frac{3}{4} = \frac{3}{5} \longrightarrow \underline{P_{untersch. Farben}(B/R)=60\%} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b)\: Weise\: nach,\: dass\: die\: Spielerin,\: die\: die\: 1.\: Kugel\: entnimmt,\: einen\: Vorteil\: hat $
$\qquad\:\:$ Für die Wahrscheinlichkeit dafür, dass die Spielerin gewinnt, die die 1. Kugel entnimmt, gilt:
$\qquad\qquad$ $ \frac{2}{5} + \frac{3}{5} \cdot \frac{2}{4} \cdot \frac{2}{3} = \frac{3}{5}>\frac{1}{2} $
$\qquad\:\:$ $ P_{untersch. Farben}(B/R) = \frac{3}{5} \cdot \frac{2}{4} + \frac{2}{5} \cdot \frac{3}{4} = \frac{3}{5} \longrightarrow \underline{P_{untersch. Farben}(B/R)=60\%} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize b)\: Weise\: nach,\: dass\: die\: Spielerin,\: die\: die\: 1.\: Kugel\: entnimmt,\: einen\: Vorteil\: hat $
$\qquad\:\:$ Für die Wahrscheinlichkeit dafür, dass die Spielerin gewinnt, die die 1. Kugel entnimmt, gilt:
$\qquad\qquad$ $ \frac{2}{5} + \frac{3}{5} \cdot \frac{2}{4} \cdot \frac{2}{3} = \frac{3}{5}>\frac{1}{2} $
Zentralabitur 2020 - Mathe Grundkurs - Teil 2 - Exponentialfunktion
Zentralabitur 2020 – Mathe Grundkurs – Teil2 – Exponentialfunktion
Aufgabe 2.1 Exponentialfunktion

Lösung a)
$
f(x)=(6x-3)e^{-x},\:\: x\in \mathbb{R}.
$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize a)\: Schnittpunkte\: des\: Graphen\: von\: f\: mit\: den\: Koordinaten $
$\qquad\:\:$ * Schnittpunkte mit der $x-Achse$ (Nullstellen) $y=f(x)=0$
$\qquad\qquad$ $ \iff (6x-3)\cdot e^{-x}=0 \Longrightarrow \begin{cases} (6x-3)=0\:\: \textcolor{red}{|+3} \:\: \longrightarrow x=\frac{1}{2}\\ \\ e^{-x}=0\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Es gibt ein Schnittpunkt mit der $x-Achse$ an der Stelle $\underline{S_x=(\frac{1}{2}|0})$
$\qquad\:\:$ * Schnittpunkte mit der $y-Achse$ $\longrightarrow y=f(0)$
$\qquad\qquad$ $ \iff y=[6(0)-3]\cdot e^{-0}=-3 $
$\qquad\qquad$ Es gibt ein Schnittpunkt mit der $y-Achse$ an der Stelle $\underline{S_y=(0|-3})$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize a)\: Schnittpunkte\: des\: Graphen\: von\: f\: mit\: den\: Koordinaten $
$\qquad\:\:$ * Schnittpunkte mit der $x-Achse$ (Nullstellen) $y=f(x)=0$
$\qquad\qquad$ $ \iff (6x-3)\cdot e^{-x}=0 \Longrightarrow \begin{cases} (6x-3)=0\:\: \textcolor{red}{|+3} \:\: \longrightarrow x=\frac{1}{2}\\ \\ e^{-x}=0\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Es gibt ein Schnittpunkt mit der $x-Achse$ an der Stelle $\underline{S_x=(\frac{1}{2}|0})$
$\qquad\:\:$ * Schnittpunkte mit der $y-Achse$ $\longrightarrow y=f(0)$
$\qquad\qquad$ $ \iff y=[6(0)-3]\cdot e^{-0}=-3 $
$\qquad\qquad$ Es gibt ein Schnittpunkt mit der $y-Achse$ an der Stelle $\underline{S_y=(0|-3})$
Lösung b)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
b)\: Verhalten\: der\: Funktionswerte\: von\: f\: für\: x\rightarrow +\infty\: und\: x\rightarrow -\infty\: an
$
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=-\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=-\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $
Lösung c)
$
f(x)=(6x-3)e^{-x}
$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize c)\: Weise\: nach,\: dass\: die\: 1.\: Ableitung\: f^\prime(x)=(-6x+9)e^{-x}\: ist $
$\qquad\:\:$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x) \Longrightarrow \begin{cases} u(x)=(6x-3)\: \longrightarrow u^\prime(x)=6\\ \\ v(x)=e^{-x}\: \longrightarrow v^\prime(x)=-e^{-x} \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=6\cdot e^{-x}+(6x-3)\cdot (-e^{-x})=\underline{(-6x+9)\cdot e^{-x}}\:\: W.A. $
$\qquad\:\:$ Lokaler Extrempunkt von $f$
$\qquad\qquad$ $ f^\prime(x)=0 \iff \begin{cases} (-6x+9)=0\:\: \textcolor{red}{|-9}\:\: \longrightarrow x=\frac{3}{2}\\ \\ e^{-x}=0\:\: \longrightarrow \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Es gibt eine Extremstelle an der Stelle $\underline{x=\frac{3}{2}}$
$\qquad\:\:$ $ \iff $ Der lokale Extrempunkt lautet: $ \underline{ E \begin{bmatrix} \frac{3}{2}| f(\frac{3}{2}) \end{bmatrix} = \begin{pmatrix} 1,5| 1,34 \end{pmatrix} } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize c)\: Weise\: nach,\: dass\: die\: 1.\: Ableitung\: f^\prime(x)=(-6x+9)e^{-x}\: ist $
$\qquad\:\:$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x) \Longrightarrow \begin{cases} u(x)=(6x-3)\: \longrightarrow u^\prime(x)=6\\ \\ v(x)=e^{-x}\: \longrightarrow v^\prime(x)=-e^{-x} \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=6\cdot e^{-x}+(6x-3)\cdot (-e^{-x})=\underline{(-6x+9)\cdot e^{-x}}\:\: W.A. $
$\qquad\:\:$ Lokaler Extrempunkt von $f$
$\qquad\qquad$ $ f^\prime(x)=0 \iff \begin{cases} (-6x+9)=0\:\: \textcolor{red}{|-9}\:\: \longrightarrow x=\frac{3}{2}\\ \\ e^{-x}=0\:\: \longrightarrow \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Es gibt eine Extremstelle an der Stelle $\underline{x=\frac{3}{2}}$
$\qquad\:\:$ $ \iff $ Der lokale Extrempunkt lautet: $ \underline{ E \begin{bmatrix} \frac{3}{2}| f(\frac{3}{2}) \end{bmatrix} = \begin{pmatrix} 1,5| 1,34 \end{pmatrix} } $
Lösung d)
Die Funktionswerte der 1. Ableitungsfunktion von $f$ sind
$\qquad\qquad$ $ \begin{cases} – für\: x<\frac{3}{2}\: positiv\\ \\ - für\: x>\frac{3}{2}\: negativ \end{cases} \iff $ Es liegt ein lokales Maximum vor.
$\qquad\qquad$ $ \begin{cases} – für\: x<\frac{3}{2}\: positiv\\ \\ - für\: x>\frac{3}{2}\: negativ \end{cases} \iff $ Es liegt ein lokales Maximum vor.
Lösung e)

Lösung f)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
c)\: Gleichung der\: Tangente\: t\: im\: Punkt\: P(1|f(1))
$
$\qquad\:\:$ Formel: $t(x)=f^\prime(1)(x-1)+f(1)$ mit $ \begin{cases} x=1\\ \\ f^\prime(1)=3e^{-1}\\ \\ f(1)=3e^{-1} \end{cases} $
$\qquad\qquad$ $ \Longrightarrow t(x)=3e^{-1}(x-1)+3e^{-1} = 3e^{-1}\cdot x-3e^{-1}+3e^{-1}=\underline{3e^{-1}\cdot x} $
$\qquad\:\:$ Schnittwinkel mit der $x-Achse$
$\qquad\qquad$ $tan(\alpha)=f^\prime(1) \iff \alpha=tan^{-1}(3e^{-1}) \longrightarrow \underline{\alpha=47,82^{\circ}}$
$\qquad\:\:$ Formel: $t(x)=f^\prime(1)(x-1)+f(1)$ mit $ \begin{cases} x=1\\ \\ f^\prime(1)=3e^{-1}\\ \\ f(1)=3e^{-1} \end{cases} $
$\qquad\qquad$ $ \Longrightarrow t(x)=3e^{-1}(x-1)+3e^{-1} = 3e^{-1}\cdot x-3e^{-1}+3e^{-1}=\underline{3e^{-1}\cdot x} $
$\qquad\:\:$ Schnittwinkel mit der $x-Achse$
$\qquad\qquad$ $tan(\alpha)=f^\prime(1) \iff \alpha=tan^{-1}(3e^{-1}) \longrightarrow \underline{\alpha=47,82^{\circ}}$
Lösung g)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
g)\: Berechne \: X_M\: und\: den\: Abstand\: der\: beiden\: Graphen\: von\: f\: und\: f^\prime
$
$\qquad\:\:$ Der senkrechte Abstand der Graphen von $f$ und $f^\prime$ wird maximal mit
$\qquad\qquad$ $g(x)=f(x)-f^\prime(x)$
$\qquad\qquad\qquad$ $ =(6x-3)e^{-x}-[(-6x+9)e^{-x}] $
$\qquad\qquad\qquad$ $ =(12x-12)e^{-x} $
$\qquad\qquad$ $g^\prime(x)$ mit Produktregel bestimmen
$\qquad\qquad\qquad$ $ g^\prime(x)=12\cdot e^{-x}+(12x-12)\cdot (-e^{-x})=(-12x+24)\cdot e^{-x} $
$\qquad\qquad$ Extremstelle $X_M$ berechnen
$\qquad\qquad\qquad$ $ g^\prime(x)=0 \iff (-12x+24)\cdot e^{-x} \Longrightarrow \begin{cases} (-12x+24)=0\:\: \textcolor{red}{|-24}\:\: \longrightarrow x_M=2\\ \\ e^{-x}=0\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Der Abstand ist an der Stelle $\underline{X_M=2}$ maximal
$\qquad\qquad$ Dieser Abstand beträgt: $g(2)=[12(2)-12]\cdot e^{-2}=\underline{1,624\: LE}$
$\qquad\:\:$ Der senkrechte Abstand der Graphen von $f$ und $f^\prime$ wird maximal mit
$\qquad\qquad$ $g(x)=f(x)-f^\prime(x)$
$\qquad\qquad\qquad$ $ =(6x-3)e^{-x}-[(-6x+9)e^{-x}] $
$\qquad\qquad\qquad$ $ =(12x-12)e^{-x} $
$\qquad\qquad$ $g^\prime(x)$ mit Produktregel bestimmen
$\qquad\qquad\qquad$ $ g^\prime(x)=12\cdot e^{-x}+(12x-12)\cdot (-e^{-x})=(-12x+24)\cdot e^{-x} $
$\qquad\qquad$ Extremstelle $X_M$ berechnen
$\qquad\qquad\qquad$ $ g^\prime(x)=0 \iff (-12x+24)\cdot e^{-x} \Longrightarrow \begin{cases} (-12x+24)=0\:\: \textcolor{red}{|-24}\:\: \longrightarrow x_M=2\\ \\ e^{-x}=0\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Der Abstand ist an der Stelle $\underline{X_M=2}$ maximal
$\qquad\qquad$ Dieser Abstand beträgt: $g(2)=[12(2)-12]\cdot e^{-2}=\underline{1,624\: LE}$
Lösung h)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
h)
$
$\qquad\qquad$ F ist eine Stammfunktion der Funktion f, wenn $F^\prime(x)=f(x)$
$\qquad\qquad$ Leite $F(x)=(-6x-3)\cdot e^{-x}$ mit dem Produktregel ab
$\qquad\qquad\qquad$ $ H(x)=(-6)\cdot e^{-x}+(-6x-3)\cdot (-e^{-x}) $
$\qquad\qquad\qquad$ $ =(6x-3)\cdot e^{-x}+20\:\: |\:\: Probe:\: H(0)=[6(0)-3]e^{-0}+20=17 $
$\qquad\qquad$ Die Gleichung der gesuchten Stammfunktion H ist: $\underline{H(x)=(6x-3)\cdot e^{-x}+20}$
$\qquad\qquad$ F ist eine Stammfunktion der Funktion f, wenn $F^\prime(x)=f(x)$
$\qquad\qquad$ Leite $F(x)=(-6x-3)\cdot e^{-x}$ mit dem Produktregel ab
$\qquad\qquad\qquad$ $ H(x)=(-6)\cdot e^{-x}+(-6x-3)\cdot (-e^{-x}) $
$\qquad\qquad\qquad$ $ =(6x-3)\cdot e^{-x}+20\:\: |\:\: Probe:\: H(0)=[6(0)-3]e^{-0}+20=17 $
$\qquad\qquad$ Die Gleichung der gesuchten Stammfunktion H ist: $\underline{H(x)=(6x-3)\cdot e^{-x}+20}$
Lösung i)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
i)\: Ermittle\: den\: Flächeninhalt\: der\: Fläche\: zwischen\: f\: und\: die\: x-Achse
$
$\qquad\:\:$ $ \int\limits_{1}^{5} \begin{bmatrix} \begin{pmatrix} 6x-3 \end{pmatrix} \cdot e^{-x} \end{bmatrix} dx = \begin{bmatrix} \begin{pmatrix} -6x-3 \end{pmatrix} \cdot e^{-x} \end{bmatrix} _1 ^{5} = -33e^{-5}-(-9e^{-1})\approx3,09 $
$\qquad\:\:$ Der Inhalt der Fläche beträgt ca. $\underline{3,1\: FE}$
$\qquad\:\:$ $ \int\limits_{1}^{5} \begin{bmatrix} \begin{pmatrix} 6x-3 \end{pmatrix} \cdot e^{-x} \end{bmatrix} dx = \begin{bmatrix} \begin{pmatrix} -6x-3 \end{pmatrix} \cdot e^{-x} \end{bmatrix} _1 ^{5} = -33e^{-5}-(-9e^{-1})\approx3,09 $
$\qquad\:\:$ Der Inhalt der Fläche beträgt ca. $\underline{3,1\: FE}$
Lösung j)
$
\:\:\:
$
$
\:
\Large
\Bigg\downarrow
$
$
\normalsize
j)
$
$\qquad\:\:$ Es muss $f^\prime(x)=f^{\prime\prime}(x)$ gelten, wenn es eine Stelle $X_T$ gibt, an der die Tangente an
$\qquad\:\:$ der Graphen von $f$ Parallel zu der Tangente an den Graphen von $f^\prime$ verläuft.
$\qquad\qquad$ Berechne $f^{\prime\prime}(x)$ mit Produktregel
$\qquad\qquad\:\:\:\:$ $ f^{\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\: | \begin{cases} u(x)=(-6x+9)\:\: \longrightarrow\: u^\prime(x)=-6\\ \\ v(x)=e^{-x}\:\: \longrightarrow\: v^\prime(x)=-e^{-x} \end{cases} $
$\qquad\qquad\:\:\:\:$ $ \iff f^{\prime\prime}(x)=(-6)\cdot e^{-x}+(-6x+9)\cdot (-e^{-x}) $
$\qquad\qquad\qquad\qquad\qquad\:$ $ =(-6x-15)\cdot e^{-x} $
$\qquad\:\:$ $ f^\prime(x)=f^{\prime\prime}(x) \iff (-6x+9)\cdot e^{-x}=(-6x-15)\cdot e^{-x} \iff x=2 $
$\qquad\:\:$ An der Stelle $X_T=2$ ist die Tangente an den Graphen von $f$ parallel zur Tangente
$\qquad\:\:$ an den Graphen von $f^\prime$.
$\qquad\:\:$ Es muss $f^\prime(x)=f^{\prime\prime}(x)$ gelten, wenn es eine Stelle $X_T$ gibt, an der die Tangente an
$\qquad\:\:$ der Graphen von $f$ Parallel zu der Tangente an den Graphen von $f^\prime$ verläuft.
$\qquad\qquad$ Berechne $f^{\prime\prime}(x)$ mit Produktregel
$\qquad\qquad\:\:\:\:$ $ f^{\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\: | \begin{cases} u(x)=(-6x+9)\:\: \longrightarrow\: u^\prime(x)=-6\\ \\ v(x)=e^{-x}\:\: \longrightarrow\: v^\prime(x)=-e^{-x} \end{cases} $
$\qquad\qquad\:\:\:\:$ $ \iff f^{\prime\prime}(x)=(-6)\cdot e^{-x}+(-6x+9)\cdot (-e^{-x}) $
$\qquad\qquad\qquad\qquad\qquad\:$ $ =(-6x-15)\cdot e^{-x} $
$\qquad\:\:$ $ f^\prime(x)=f^{\prime\prime}(x) \iff (-6x+9)\cdot e^{-x}=(-6x-15)\cdot e^{-x} \iff x=2 $
$\qquad\:\:$ An der Stelle $X_T=2$ ist die Tangente an den Graphen von $f$ parallel zur Tangente
$\qquad\:\:$ an den Graphen von $f^\prime$.
Kurvendiskussion e-Funktion
Kurvendiskussion e-Funktion
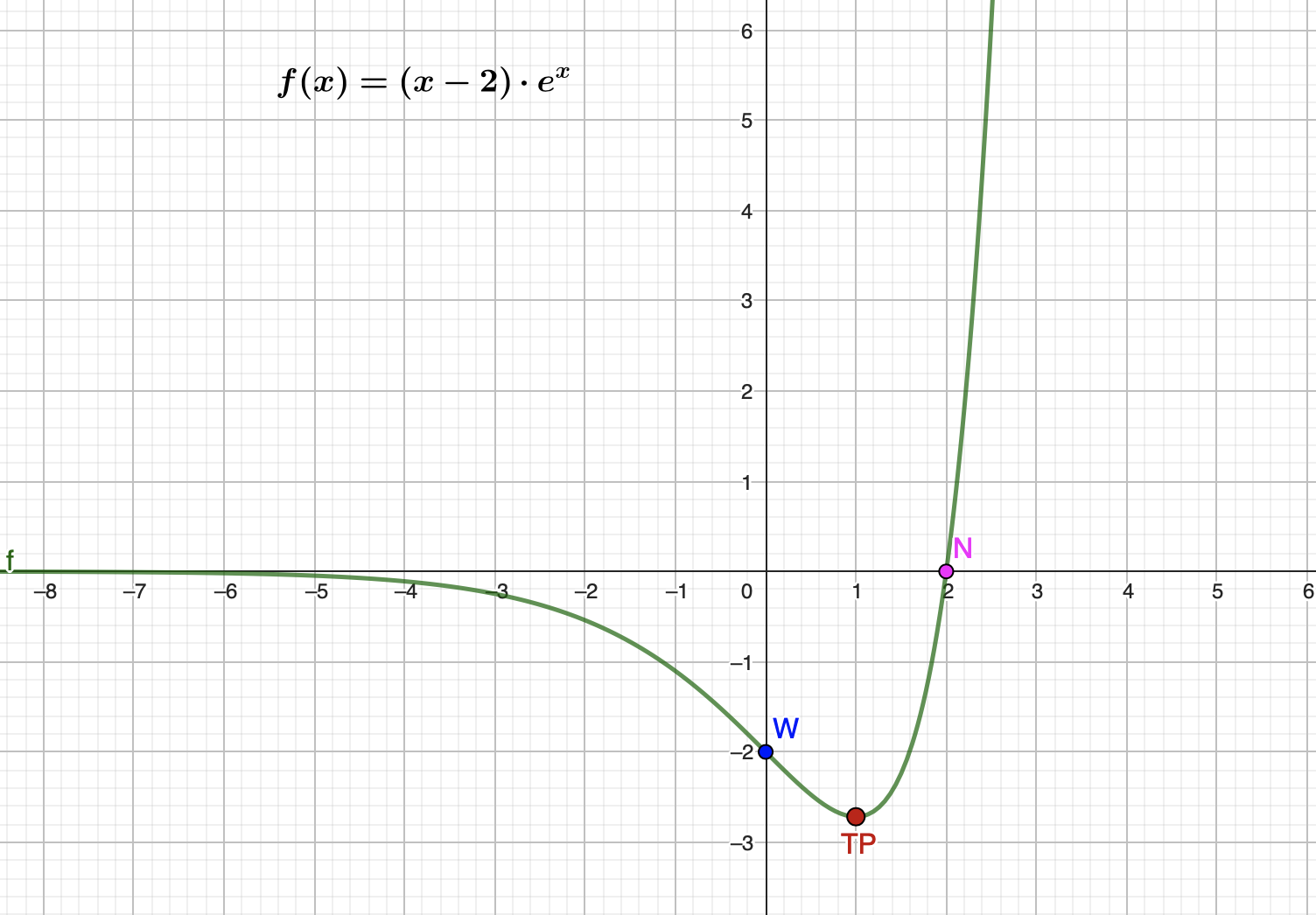
$f(x)=(x-2) \cdot e^{x} $
Lösung
$f(x)=(x-2)
\cdot
e^{x}
$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln\: (Es\: geht\: um\: die\: x-Achse) $
$\qquad$ $ f(-1)=(-1-2) \cdot e^{-1} = -3\cdot e^{-1} =-1,103 $
$\qquad\qquad$ $ \iff $ $\forall x<0$, gibt eine $y$-Werte und die Funktion ist definiert!
$\qquad$ $ f(1)=(1-2) \cdot e^{1} = -1\cdot e^{1} =-e=-2,71 $
$\qquad\qquad$ $ \iff $ $\forall x>0$, gibt eine $y$-Werte und die Funktion ist definiert!
$\qquad$ Die Funktion ist auf beiden Seiten der $x$-Achse definiert.
$\qquad\qquad$ $\Longrightarrow$ $ \textbf {Die Definitionsbereich lautet:} $ $D_{f}=\mathbb{R}=] -\infty; + \infty[$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Nullstellen\: berechnen\: [Ansatz: \: f(x)=0] $
$\qquad$ $ (x-2)\cdot e^{x}=0 \iff \begin{cases} (x-2)=0\:\: \textcolor{red}{|+2}\:\: \longrightarrow x=2\\ oder\\ e^{x}=0,\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ $\Longrightarrow$ $ \textbf { Die Funktion $f$ hat eine Nullstelle bei $x=2$. } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: y-Achsenabschnitt\: berechnen\: [Ansatz: \: y=f(0)] $
$\qquad$ $ y=f(x)=(x-2) \cdot e^{x} $
$\qquad$ $ y=f(0)=(0-2) \cdot e^{0} =-2 \cdot 1=-2 $
$\qquad\qquad$ $\Longrightarrow$ $ \textbf { Die Funktion $f$ schneidet die $y$-Achse in dem Punkt $(0|-2)$. } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Verhalten\: im\: Unendlichen\: bestimmen $
$\qquad$ $ \lim\limits_{x \to -\infty} (x-2)\cdot e^{x} = \lim\limits_{x \to -\infty} e^{x} =0 $ $ \:\:\: | \:\:\: $ $ \lim\limits_{x \to +\infty} (x-2)\cdot e^{x} = \lim\limits_{x \to +\infty} e^{x} =+\infty $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Symmetrieverhalten\: bestimmen $
$\qquad$ Symmetriearten:
$\qquad\qquad$ – Achsensymmetrie zur $y$-Achse: $f(-x)=f(x)$
$\qquad\qquad$ – Punktsymmetrie zur Ursprung: $f(-x)=-f(x)$
$\qquad\qquad$ $ f(-x)=(-x-2) \cdot e^{-x} \neq f(x) \:\: \Longrightarrow $ kein Achsensymmetrie zu $y$-Achse
$\qquad\qquad\qquad\:\:\:\:$ $ = -(x+2) \cdot e^{-x} \neq -f(x) \:\: \Longrightarrow $ kein Punktsymmetrie zum Ursprung
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Extrempunkte\: berechnen $
$\qquad$ Extremstellen berechnen
$\qquad\qquad$ – An Hochpunkte gilt: $f^\prime(x)=0$ und $f^{\prime\prime}(x)<0$
$\qquad\qquad$ – An Tiefpunkte gilt: $\:\:\:f^\prime(x)=0$ und $f^{\prime\prime}(x)>0$
$\qquad$ 1. und 2. Ableitungen (Produktregel)
$\qquad\qquad$ $u(x)=(x-2) \longrightarrow u^\prime(x)=1 \:\:|\:\: v(x)=e^{x} \longrightarrow v^\prime(x)=e^{x}$
$\qquad\qquad$ $\textcolor{red}{* f^\prime(x)=u^\prime(x)\cdot v(x) + u(x)\cdot v^\prime(x)}$
$\qquad\qquad\qquad\:\:\:\:$ $ = 1\cdot e^{x}+(x-2) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = (1+x-2) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = \textcolor{red} { (x-1) \cdot e^{x} } $
$\qquad\qquad$ $t(x)=(x-1) \longrightarrow t^\prime(x)=1 \:\:|\:\: w(x)=e^{x} \longrightarrow w^\prime(x)=e^{x}$
$\qquad\qquad$ $\textcolor{blue}{* f^{\prime\prime}(x)=t^\prime(x)\cdot w(x) + t(x)\cdot w^\prime(x)}$
$\qquad\qquad\qquad\:\:\:\:$ $ = 1\cdot e^{x}+(x-1) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = (1+x-1) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = \textcolor{blue} { x \cdot e^{x} } $
$\qquad$ Nullstelle der ersten Ableitung
$\qquad\qquad$ $ f^\prime(x)=0 $
$\qquad\qquad$ $ (x-1)\cdot e^{x}=0 \iff \begin{cases} (x-1)=0\:\: \textcolor{red}{|+1} \longrightarrow x=1\\ oder\\ e^{x}=0,\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Potentielle Extremstelle bei $x=1$
$\qquad\qquad$ Potentielle Extremstelle in 2. Ableitung einsetzen
$\qquad\qquad\qquad$ $ f^{\prime\prime}(x)= f^{\prime\prime}(1)=1\cdot e^{1} \approx 2,71>0 \iff Tiefpunkt $
$\qquad\qquad$ Extremstellen in ursprüngliche Funktion einsetzen
$\qquad\qquad\qquad$ $f(1)=(1-2)\cdot e^{1}=-e \approx -2,71$
$\qquad$ $ \textbf { Der Tiefpunkt lautet: $T_p(1|-e)$ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Monotonieverhalten\: bestimmen $
$\qquad\qquad$
– Im Intervall von $]-\infty;1[$, fällt der Graph von $f(x)$ streng monoton.
$\qquad\qquad$ – Im Intervall von $]1;+\infty[$, steigt der Graph von $f(x)$ streng monoton.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkt\: und\: Wendetangente\: berechnen\: [Ansatz:\: f^{\prime\prime}(x)=0\: und\: f^{\prime\prime\prime}(x)\neq0] $
$\qquad\qquad$ 3. Abteilung (Produktregel)
$\qquad\qquad\qquad$ $y(x)=x \longrightarrow y^\prime(x)=1\:\: | \:\: z(x)=e^{x} \longrightarrow z^\prime(x)=e^{x}$
$\qquad\qquad\qquad$ $\textcolor{green}{* f^{\prime\prime\prime}(x)=y^\prime(x)\cdot z(x) + y(x)\cdot z^\prime(x)}$
$\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ = 1\cdot e^{x}+x\cdot e^{x} $
$\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ = \textcolor{green}{(1+x)\cdot e^{x}} $
$\qquad\qquad$ Nullstelle der zweite Ableitung
$\qquad\qquad\qquad$ $f^{\prime\prime}(x)=0$
$\qquad\qquad\qquad$ $x\cdot e^{x}=0 \iff \begin{cases} x=0\\ oder\\ e^{x}=0,\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad\qquad$ Potentielle Wendestelle in 3. Ableitung einsetzen
$\qquad\qquad\qquad\qquad$ $f^{\prime\prime\prime}(x)=f^{\prime\prime\prime}(0)=(1+0)\cdot e^{0}=1\neq0$
$\qquad\qquad\qquad\qquad$ $\iff Wendepunkt$ an der Stelle $x=0$
$\qquad\qquad\qquad$ Wendestelle in ursprüngliche Funktion einsetzen
$\qquad\qquad\qquad\qquad$ $f(0)=(0-2)\cdot e^{0}=-2$
$\qquad$ $ \textbf{ Der Wendepunkt lautet:}\: W_p(0|-2) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: Finden $
$\qquad$ Gleichung der Wendetangente:
$\qquad\:\:$ $t_w:\: f(x_0)=f^\prime(x_0)\cdot (x-x_0)+f(x_0)$ mit $ \begin{cases} x_0=0\\ f^\prime(x_0)=m=f^\prime(0)=(0-1)\cdot e^{0}=-1\\ f(x_0)=-2 \end{cases} $
$\qquad\qquad$ $ \Longrightarrow t_w=-1(x-0)+(-2)= -x-2 $
$\qquad$ $ \textbf{ Die Wendetangente lautet: $t_w=-x-2$ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Krümmungen\: ermitteln $
$\qquad$ Linkskrümmung [Links vom Wendepunkt (x=0)]
$\qquad\qquad$ Nimm zum Beispiel die Stelle $x=+1$
$\qquad\qquad$ $f^{\prime\prime}(+1)=+1\cdot e^{+1}=e\approx2,71>0 \longrightarrow linksgekrümmt$
$\qquad$ Rechtskrümmung [Rechts vom Wendepunkt (x=0)]
$\qquad\qquad$ Nimm zum Beispiel die Stelle $x=-1$
$\qquad\qquad$ $f^{\prime\prime}(-1)=-1\cdot e^{-1}=e\approx-0,37<0 \longrightarrow rechtsgekrümmt$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 11.\: Wertebereich\: bestimmen $
$\qquad$ Mit einem Tiefpunkt bei $(1|-e)$ und den Grenzwert $+\infty$,
$\qquad$ Lautet den Wertebereich: $\mathbb{W}=[-e;+\infty[$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 12.\: Funktionsgraph\: zeichnen $
$\qquad$ Wertetabelle erstellen
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln\: (Es\: geht\: um\: die\: x-Achse) $
$\qquad$ $ f(-1)=(-1-2) \cdot e^{-1} = -3\cdot e^{-1} =-1,103 $
$\qquad\qquad$ $ \iff $ $\forall x<0$, gibt eine $y$-Werte und die Funktion ist definiert!
$\qquad$ $ f(1)=(1-2) \cdot e^{1} = -1\cdot e^{1} =-e=-2,71 $
$\qquad\qquad$ $ \iff $ $\forall x>0$, gibt eine $y$-Werte und die Funktion ist definiert!
$\qquad$ Die Funktion ist auf beiden Seiten der $x$-Achse definiert.
$\qquad\qquad$ $\Longrightarrow$ $ \textbf {Die Definitionsbereich lautet:} $ $D_{f}=\mathbb{R}=] -\infty; + \infty[$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Nullstellen\: berechnen\: [Ansatz: \: f(x)=0] $
$\qquad$ $ (x-2)\cdot e^{x}=0 \iff \begin{cases} (x-2)=0\:\: \textcolor{red}{|+2}\:\: \longrightarrow x=2\\ oder\\ e^{x}=0,\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ $\Longrightarrow$ $ \textbf { Die Funktion $f$ hat eine Nullstelle bei $x=2$. } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: y-Achsenabschnitt\: berechnen\: [Ansatz: \: y=f(0)] $
$\qquad$ $ y=f(x)=(x-2) \cdot e^{x} $
$\qquad$ $ y=f(0)=(0-2) \cdot e^{0} =-2 \cdot 1=-2 $
$\qquad\qquad$ $\Longrightarrow$ $ \textbf { Die Funktion $f$ schneidet die $y$-Achse in dem Punkt $(0|-2)$. } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Verhalten\: im\: Unendlichen\: bestimmen $
$\qquad$ $ \lim\limits_{x \to -\infty} (x-2)\cdot e^{x} = \lim\limits_{x \to -\infty} e^{x} =0 $ $ \:\:\: | \:\:\: $ $ \lim\limits_{x \to +\infty} (x-2)\cdot e^{x} = \lim\limits_{x \to +\infty} e^{x} =+\infty $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Symmetrieverhalten\: bestimmen $
$\qquad$ Symmetriearten:
$\qquad\qquad$ – Achsensymmetrie zur $y$-Achse: $f(-x)=f(x)$
$\qquad\qquad$ – Punktsymmetrie zur Ursprung: $f(-x)=-f(x)$
$\qquad\qquad$ $ f(-x)=(-x-2) \cdot e^{-x} \neq f(x) \:\: \Longrightarrow $ kein Achsensymmetrie zu $y$-Achse
$\qquad\qquad\qquad\:\:\:\:$ $ = -(x+2) \cdot e^{-x} \neq -f(x) \:\: \Longrightarrow $ kein Punktsymmetrie zum Ursprung
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Extrempunkte\: berechnen $
$\qquad$ Extremstellen berechnen
$\qquad\qquad$ – An Hochpunkte gilt: $f^\prime(x)=0$ und $f^{\prime\prime}(x)<0$
$\qquad\qquad$ – An Tiefpunkte gilt: $\:\:\:f^\prime(x)=0$ und $f^{\prime\prime}(x)>0$
$\qquad$ 1. und 2. Ableitungen (Produktregel)
$\qquad\qquad$ $u(x)=(x-2) \longrightarrow u^\prime(x)=1 \:\:|\:\: v(x)=e^{x} \longrightarrow v^\prime(x)=e^{x}$
$\qquad\qquad$ $\textcolor{red}{* f^\prime(x)=u^\prime(x)\cdot v(x) + u(x)\cdot v^\prime(x)}$
$\qquad\qquad\qquad\:\:\:\:$ $ = 1\cdot e^{x}+(x-2) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = (1+x-2) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = \textcolor{red} { (x-1) \cdot e^{x} } $
$\qquad\qquad$ $t(x)=(x-1) \longrightarrow t^\prime(x)=1 \:\:|\:\: w(x)=e^{x} \longrightarrow w^\prime(x)=e^{x}$
$\qquad\qquad$ $\textcolor{blue}{* f^{\prime\prime}(x)=t^\prime(x)\cdot w(x) + t(x)\cdot w^\prime(x)}$
$\qquad\qquad\qquad\:\:\:\:$ $ = 1\cdot e^{x}+(x-1) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = (1+x-1) \cdot e^{x} $
$\qquad\qquad\qquad\:\:\:\:$ $ = \textcolor{blue} { x \cdot e^{x} } $
$\qquad$ Nullstelle der ersten Ableitung
$\qquad\qquad$ $ f^\prime(x)=0 $
$\qquad\qquad$ $ (x-1)\cdot e^{x}=0 \iff \begin{cases} (x-1)=0\:\: \textcolor{red}{|+1} \longrightarrow x=1\\ oder\\ e^{x}=0,\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Potentielle Extremstelle bei $x=1$
$\qquad\qquad$ Potentielle Extremstelle in 2. Ableitung einsetzen
$\qquad\qquad\qquad$ $ f^{\prime\prime}(x)= f^{\prime\prime}(1)=1\cdot e^{1} \approx 2,71>0 \iff Tiefpunkt $
$\qquad\qquad$ Extremstellen in ursprüngliche Funktion einsetzen
$\qquad\qquad\qquad$ $f(1)=(1-2)\cdot e^{1}=-e \approx -2,71$
$\qquad$ $ \textbf { Der Tiefpunkt lautet: $T_p(1|-e)$ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Monotonieverhalten\: bestimmen $
| Funktion | $-\infty$ | 1 | $+\infty$ |
| $f^\prime(x)$ | $-$ | $\vert$ | $+$ |
| $f(x)$ | $\searrow$ | $-e$ | $\nearrow$ |
$\qquad\qquad$ – Im Intervall von $]1;+\infty[$, steigt der Graph von $f(x)$ streng monoton.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkt\: und\: Wendetangente\: berechnen\: [Ansatz:\: f^{\prime\prime}(x)=0\: und\: f^{\prime\prime\prime}(x)\neq0] $
$\qquad\qquad$ 3. Abteilung (Produktregel)
$\qquad\qquad\qquad$ $y(x)=x \longrightarrow y^\prime(x)=1\:\: | \:\: z(x)=e^{x} \longrightarrow z^\prime(x)=e^{x}$
$\qquad\qquad\qquad$ $\textcolor{green}{* f^{\prime\prime\prime}(x)=y^\prime(x)\cdot z(x) + y(x)\cdot z^\prime(x)}$
$\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ = 1\cdot e^{x}+x\cdot e^{x} $
$\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ = \textcolor{green}{(1+x)\cdot e^{x}} $
$\qquad\qquad$ Nullstelle der zweite Ableitung
$\qquad\qquad\qquad$ $f^{\prime\prime}(x)=0$
$\qquad\qquad\qquad$ $x\cdot e^{x}=0 \iff \begin{cases} x=0\\ oder\\ e^{x}=0,\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad\qquad$ Potentielle Wendestelle in 3. Ableitung einsetzen
$\qquad\qquad\qquad\qquad$ $f^{\prime\prime\prime}(x)=f^{\prime\prime\prime}(0)=(1+0)\cdot e^{0}=1\neq0$
$\qquad\qquad\qquad\qquad$ $\iff Wendepunkt$ an der Stelle $x=0$
$\qquad\qquad\qquad$ Wendestelle in ursprüngliche Funktion einsetzen
$\qquad\qquad\qquad\qquad$ $f(0)=(0-2)\cdot e^{0}=-2$
$\qquad$ $ \textbf{ Der Wendepunkt lautet:}\: W_p(0|-2) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: Finden $
$\qquad$ Gleichung der Wendetangente:
$\qquad\:\:$ $t_w:\: f(x_0)=f^\prime(x_0)\cdot (x-x_0)+f(x_0)$ mit $ \begin{cases} x_0=0\\ f^\prime(x_0)=m=f^\prime(0)=(0-1)\cdot e^{0}=-1\\ f(x_0)=-2 \end{cases} $
$\qquad\qquad$ $ \Longrightarrow t_w=-1(x-0)+(-2)= -x-2 $
$\qquad$ $ \textbf{ Die Wendetangente lautet: $t_w=-x-2$ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Krümmungen\: ermitteln $
$\qquad$ Linkskrümmung [Links vom Wendepunkt (x=0)]
$\qquad\qquad$ Nimm zum Beispiel die Stelle $x=+1$
$\qquad\qquad$ $f^{\prime\prime}(+1)=+1\cdot e^{+1}=e\approx2,71>0 \longrightarrow linksgekrümmt$
$\qquad$ Rechtskrümmung [Rechts vom Wendepunkt (x=0)]
$\qquad\qquad$ Nimm zum Beispiel die Stelle $x=-1$
$\qquad\qquad$ $f^{\prime\prime}(-1)=-1\cdot e^{-1}=e\approx-0,37<0 \longrightarrow rechtsgekrümmt$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 11.\: Wertebereich\: bestimmen $
$\qquad$ Mit einem Tiefpunkt bei $(1|-e)$ und den Grenzwert $+\infty$,
$\qquad$ Lautet den Wertebereich: $\mathbb{W}=[-e;+\infty[$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 12.\: Funktionsgraph\: zeichnen $
$\qquad$ Wertetabelle erstellen
| x | -2,5 | -2 | -1 | 1 | 1,5 | 2,5 | 3 |
| f(x) | -0,3 | -0,5 | -1,1 | -2,7 | -2,2 | 6,1 | 20,1 |

$f(x)= \frac{1}{4}e^{2x} \cdot (x^2-2) $
Lösung
$f(x)=
\frac{1}{4}e^{2x} \cdot (x^2-2)
$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln\: (Es\: geht\: um\: die\: x-Achse) $
$\qquad\:\:$ $ \begin{cases} \frac{1}{4}e^{2x} \in\mathbb{R}\\ \\ (x^2-2) \in\mathbb{R} \end{cases} \Longrightarrow \:\: D_f=\mathbb{R}=]-\infty;+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln\: (Es\: geht\: um\: die\: y-Achse) $
$\qquad\:\:$ $ \forall y \in \mathbb{R}, y> -\frac{1}{4}e^{2x}\\ \:\: \Longrightarrow \:\: W_f=]-\frac{1}{4}e^{2x};+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $f(x)=\frac{1}{4}e^{2x} \cdot(x^2-2)\:\: mit \:\: \begin{cases} u(x)=\frac{1}{4}e^{2x} \:\: \longrightarrow u^\prime(x)=\frac{1}{2}e^{2x}\\ \\ v(x)=(x^2-2) \:\: \longrightarrow v^\prime(x)=2x \end{cases} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x) \cdot v(x)+u(x) \cdot v^\prime(x) = \frac{1}{2}e^{2x} \cdot (x^2-2) + \frac{1}{4}e^{2x} \cdot 2x $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:$ $ = \underline{e^{2x} \cdot (\frac{1}{2}x^{2} + \frac{1}{2}x-1)} $
$\qquad\:\:$ Zweite Ableitung: Mit Produktregel
$\qquad\qquad$ $f^{\prime\prime}(x)= \underline{e^{2x} \cdot (x^2+2x- \frac{3}{2})} $
$\qquad\:\:$ Dritte Ableitung: Mit Produktregel
$\qquad\qquad$ $f^{\prime\prime\prime}(x)= \underline{e^{2x} \cdot (2x^2+6x-1)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)= \frac{1}{4}e^{2\cdot 0} \cdot (0^2-2)= -\frac{1}{2} \longrightarrow S_y(0|- \frac{1}{2}) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\:(Schnittpunkt\: mit\: der\: x-Achse\: \longrightarrow \: y=f(x)=0) $
$\qquad\:\:$ $ f(x)=0 \iff \frac{1}{4}e^{2x} \cdot (x^2-2)=0 \iff \begin{cases} \frac{1}{4}e^{2x}=0\:\: \textcolor{red}{n.L.}\\ \\ (x^2-2)=0\:\: \textcolor{red}{|+2} \longrightarrow x^2=2\:\: \textcolor{red}{| \sqrt{…}} \end{cases} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ \longrightarrow x_{1/2}= \pm \sqrt{2} $
$\qquad\:\:$ Die Nullstellen sind: $N_1(\sqrt{2}|0)$ und $N_2(-\sqrt{2}|0)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)= \frac{1}{4}e^{2(-x)} \cdot [(-x)^2-2]= \frac{1}{4}e^{-2x} \cdot (x^2-2) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ \neq f(x) \longrightarrow keine\: Achsensymmetrie $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ \neq -f(x) \longrightarrow keine\: Punktsymmetrie $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^\prime(x)=0, f^{\prime\prime}(x) \neq0$
$\qquad\:\:$ $ f^\prime(x)=0 \iff e^{2x} \cdot (\frac{1}{2}x^2+\frac{1}{2}x-1)=0 \iff \begin{cases} e^{2x}=0\:\: \textcolor{red}{n.L.}\\ oder\\ \frac{1}{2}x^2+\frac{1}{2}x-1=0 \end{cases} $
$\qquad\:\:$ $ \frac{1}{2}x^2+\frac{1}{2}x-1=0\:\: \textcolor{red}{|\cdot2} $
$\qquad\qquad$ $ x^2+x-2=0\:\: (Löse\: mit\: p-q-Formel)\:\:\:\: |\:\:\:\: x_1=1\:\: und\:\: x_2=-2 $
$\qquad\:\:$ Es gibt Extrempunkte an der Stelle $x_1=1$ und $x_2=-2$
$\qquad\:\:$ $ f^{\prime\prime}(1)= e^{2(1)} \cdot [1^2+2(1)- \frac{3}{2}]=11,08>0 \longrightarrow Tiefpunkt $
$\qquad\:\:$ $ f^{\prime\prime}(-2)= e^{2(-2)} \cdot [(-2)^2+2(-2)- \frac{3}{2}]=-0,027<0 \longrightarrow Hochpunkt $
$\qquad\qquad$ $ TP[(1)|f(1)]= (1|-\frac{1}{4}e^2)\:\: \:\:und\:\:\:\: HP[(-2)|f(-2)]= (-2|\frac{1}{2e^4}) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0, f^{\prime\prime\prime}(x) \neq0$
$\qquad\:\:$ $ f^{\prime\prime}(x)=0 \iff e^{2x} \cdot (x^2+2x-\frac{3}{2})=0 \iff \begin{cases} e^{2x}=0\:\: \textcolor{red}{n.L.}\\ oder\\ x^2+2x-\frac{3}{2}=0 \end{cases} $
$\qquad\:\:$ $ x^2+2x-\frac{3}{2}=0\:\: (Löse\: mit\: p-q-Formel)\:\:\:\: |\:\:\:\: x_1=0,58\:\: und\:\: x_2=-2,58 $
$\qquad\:\:$ Es gibt Wendepunkte an der Stelle $x_1=0,58$ und $x_2=–2,58$
$\qquad\:\:$ $ f^{\prime\prime\prime}(0,58)=10,05>0 \longrightarrow RL-gekrümmt $
$\qquad\:\:$ $ f^{\prime\prime\prime}(-2,58)=-0,018<0 \longrightarrow LR-gekrümmt $
$\qquad\:\:$ $ W_1[(0,58)|f(0,58)]= (0,58|-1,33) $ und $ W_2[(-2,58)|f(-2,58)]= (-2,58|0,007) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w_1}: f(x_{w_1})=f^\prime(x_{w_1}) \cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=0,58\\ \\ f^\prime(x_{w_1})=-1,72 \\ \\ f(x_{w_1})=-1,33 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_1}}=-1,72(x-0,58)+(-1,33)= \underline{-1,72x-0,33} $
$\qquad\qquad$ $ t_{w_2}: f(x_{w_2})=f^\prime(x_{w_2}) \cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=-2,58\\ \\ f^\prime(x_{w_2})=0,006 \\ \\ f(x_{w_2})=0,007 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_2}}=0,006(x+2,58)+0,007= \underline{0,006x+0,02} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=0 \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)= +\infty $
$\qquad\:\:$ $ \textbf{Schaubild:} $

$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln\: (Es\: geht\: um\: die\: x-Achse) $
$\qquad\:\:$ $ \begin{cases} \frac{1}{4}e^{2x} \in\mathbb{R}\\ \\ (x^2-2) \in\mathbb{R} \end{cases} \Longrightarrow \:\: D_f=\mathbb{R}=]-\infty;+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln\: (Es\: geht\: um\: die\: y-Achse) $
$\qquad\:\:$ $ \forall y \in \mathbb{R}, y> -\frac{1}{4}e^{2x}\\ \:\: \Longrightarrow \:\: W_f=]-\frac{1}{4}e^{2x};+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $f(x)=\frac{1}{4}e^{2x} \cdot(x^2-2)\:\: mit \:\: \begin{cases} u(x)=\frac{1}{4}e^{2x} \:\: \longrightarrow u^\prime(x)=\frac{1}{2}e^{2x}\\ \\ v(x)=(x^2-2) \:\: \longrightarrow v^\prime(x)=2x \end{cases} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x) \cdot v(x)+u(x) \cdot v^\prime(x) = \frac{1}{2}e^{2x} \cdot (x^2-2) + \frac{1}{4}e^{2x} \cdot 2x $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:$ $ = \underline{e^{2x} \cdot (\frac{1}{2}x^{2} + \frac{1}{2}x-1)} $
$\qquad\:\:$ Zweite Ableitung: Mit Produktregel
$\qquad\qquad$ $f^{\prime\prime}(x)= \underline{e^{2x} \cdot (x^2+2x- \frac{3}{2})} $
$\qquad\:\:$ Dritte Ableitung: Mit Produktregel
$\qquad\qquad$ $f^{\prime\prime\prime}(x)= \underline{e^{2x} \cdot (2x^2+6x-1)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)= \frac{1}{4}e^{2\cdot 0} \cdot (0^2-2)= -\frac{1}{2} \longrightarrow S_y(0|- \frac{1}{2}) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\:(Schnittpunkt\: mit\: der\: x-Achse\: \longrightarrow \: y=f(x)=0) $
$\qquad\:\:$ $ f(x)=0 \iff \frac{1}{4}e^{2x} \cdot (x^2-2)=0 \iff \begin{cases} \frac{1}{4}e^{2x}=0\:\: \textcolor{red}{n.L.}\\ \\ (x^2-2)=0\:\: \textcolor{red}{|+2} \longrightarrow x^2=2\:\: \textcolor{red}{| \sqrt{…}} \end{cases} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ \longrightarrow x_{1/2}= \pm \sqrt{2} $
$\qquad\:\:$ Die Nullstellen sind: $N_1(\sqrt{2}|0)$ und $N_2(-\sqrt{2}|0)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)= \frac{1}{4}e^{2(-x)} \cdot [(-x)^2-2]= \frac{1}{4}e^{-2x} \cdot (x^2-2) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ \neq f(x) \longrightarrow keine\: Achsensymmetrie $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:$ $ \neq -f(x) \longrightarrow keine\: Punktsymmetrie $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^\prime(x)=0, f^{\prime\prime}(x) \neq0$
$\qquad\:\:$ $ f^\prime(x)=0 \iff e^{2x} \cdot (\frac{1}{2}x^2+\frac{1}{2}x-1)=0 \iff \begin{cases} e^{2x}=0\:\: \textcolor{red}{n.L.}\\ oder\\ \frac{1}{2}x^2+\frac{1}{2}x-1=0 \end{cases} $
$\qquad\:\:$ $ \frac{1}{2}x^2+\frac{1}{2}x-1=0\:\: \textcolor{red}{|\cdot2} $
$\qquad\qquad$ $ x^2+x-2=0\:\: (Löse\: mit\: p-q-Formel)\:\:\:\: |\:\:\:\: x_1=1\:\: und\:\: x_2=-2 $
$\qquad\:\:$ Es gibt Extrempunkte an der Stelle $x_1=1$ und $x_2=-2$
$\qquad\:\:$ $ f^{\prime\prime}(1)= e^{2(1)} \cdot [1^2+2(1)- \frac{3}{2}]=11,08>0 \longrightarrow Tiefpunkt $
$\qquad\:\:$ $ f^{\prime\prime}(-2)= e^{2(-2)} \cdot [(-2)^2+2(-2)- \frac{3}{2}]=-0,027<0 \longrightarrow Hochpunkt $
$\qquad\qquad$ $ TP[(1)|f(1)]= (1|-\frac{1}{4}e^2)\:\: \:\:und\:\:\:\: HP[(-2)|f(-2)]= (-2|\frac{1}{2e^4}) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0, f^{\prime\prime\prime}(x) \neq0$
$\qquad\:\:$ $ f^{\prime\prime}(x)=0 \iff e^{2x} \cdot (x^2+2x-\frac{3}{2})=0 \iff \begin{cases} e^{2x}=0\:\: \textcolor{red}{n.L.}\\ oder\\ x^2+2x-\frac{3}{2}=0 \end{cases} $
$\qquad\:\:$ $ x^2+2x-\frac{3}{2}=0\:\: (Löse\: mit\: p-q-Formel)\:\:\:\: |\:\:\:\: x_1=0,58\:\: und\:\: x_2=-2,58 $
$\qquad\:\:$ Es gibt Wendepunkte an der Stelle $x_1=0,58$ und $x_2=–2,58$
$\qquad\:\:$ $ f^{\prime\prime\prime}(0,58)=10,05>0 \longrightarrow RL-gekrümmt $
$\qquad\:\:$ $ f^{\prime\prime\prime}(-2,58)=-0,018<0 \longrightarrow LR-gekrümmt $
$\qquad\:\:$ $ W_1[(0,58)|f(0,58)]= (0,58|-1,33) $ und $ W_2[(-2,58)|f(-2,58)]= (-2,58|0,007) $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w_1}: f(x_{w_1})=f^\prime(x_{w_1}) \cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=0,58\\ \\ f^\prime(x_{w_1})=-1,72 \\ \\ f(x_{w_1})=-1,33 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_1}}=-1,72(x-0,58)+(-1,33)= \underline{-1,72x-0,33} $
$\qquad\qquad$ $ t_{w_2}: f(x_{w_2})=f^\prime(x_{w_2}) \cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=-2,58\\ \\ f^\prime(x_{w_2})=0,006 \\ \\ f(x_{w_2})=0,007 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_2}}=0,006(x+2,58)+0,007= \underline{0,006x+0,02} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=0 \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)= +\infty $
$\qquad\:\:$ $ \textbf{Schaubild:} $

$f(x)=e^{1-x^2}$
Lösung
$f(x)=e^{1-x^2}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ D_f=\forall x\in\mathbb{R}, -\infty < x < +\infty \longrightarrow D_f=]-\infty;+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ W_f=\forall y \in\mathbb{R}, 0 < y < e \longrightarrow W_f=]0;e[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $ f(x)=e^{1-x^2} $
$\qquad\qquad$ Mit Kettenregel: $ f^\prime(x)=(1-x^2)^\prime \cdot e^{1-x^2}= \underline{-2x \cdot e^{1-x^2}} $
$\qquad\:\:$ Zweite Ableitung:
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^\prime(x) \cdot v(x)+ u(x) \cdot v^\prime(x)| \begin{cases} u(x)=-2x \longrightarrow u^\prime(x)=-2\\ \\ v(x)=e^{1-x^2} \longrightarrow v^\prime(x)=-2x\cdot e^{1-x^2} \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-2\cdot e^{1-x^2}+ (-2x)\cdot (-2x) \cdot e^{1-x^2}=-2\cdot e^{1-x^2}+ 4x^2\cdot e^{1-x^2} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad$ $ =\underline{(-1+2x^2)\cdot 2e^{1-x^2}} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ Mit Produktregel und Kettenregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=u^\prime(x) \cdot v(x)+ u(x) \cdot v^\prime(x)| \begin{cases} u(x)=-1+2x^2 \longrightarrow u^\prime(x)=4x\\ \\ v(x)=2e^{1-x^2} \longrightarrow v^\prime(x)=-4x\cdot e^{1-x^2} \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=4x\cdot 2e^{1-x^2}+ (-1+2x^2)\cdot (-4x) \cdot e^{1-x^2}=4e^{1-x^2}(2x+1x-2x^3) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ =\underline{4e^{1-x^2}(3x-2x^3)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=e^{1-0^2}=e \longrightarrow \underline{S_y(0|e)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\:Nullstellen\: (Schnittpunkt\: mit\: der\: x-Achse: \longrightarrow y=f(x)=0) $
$\qquad\:\:$ $ f(x)=0 \iff e^{1-x^2}=0\:\: \textcolor{red}{n.L.}\:\: \longrightarrow keine Nullstellen $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\:Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=e^{1-(-x)^2}=e^{1-x^2}=f(x) \longrightarrow Gerade\: Funktion, Achsensymmetrie $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\:Extrempunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^\prime(x)=0, f^{\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^\prime(x)=0 \iff -2x\cdot e^{1-x^2}=0 \iff \begin{cases} -2x=0 \longrightarrow x=0\\ \\ e^{1-x^2}=0\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Es gibt ein Extrempunkt an der Stelle $x=0$
$\qquad\qquad$ $ f^{\prime\prime}(0)=[-1+2(0)^2]\cdot 2e^{1-0^2}=-2e<0 \longrightarrow Hochpunkt $
$\qquad\qquad\qquad\qquad\qquad$ $ \underline{HP[(0)|f(0)]=(0|e)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\:Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0, f^{\prime\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^{\prime\prime}(x)=0 \iff (-1+2x^2)\cdot 2e^{1-x^2}=0 $
$\qquad\qquad$ $ \iff \begin{cases} -1+2x^2=0\: \textcolor{red}{|+1}, 2x^2=1\: \textcolor{red}{|:2}, x^2=\frac{1}{2}\: \textcolor{red}{|\sqrt{…}}\: \longrightarrow \: \begin{cases} x_1=-0,707\\ \\ x_2=+0,707 \end{cases} \\ \\ 2e^{1-x^2}=0\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Es gibt Wendepunkte an der Stelle $x_1=-0,707$ und $x_2=+0,707$
$\qquad\qquad$ $ f^{\prime\prime\prime}(-0,707)=-9,33<0 \longrightarrow LR-gekrümmt $
$\qquad\qquad$ $ f^{\prime\prime\prime}(+0,707)=+9,33>0 \longrightarrow RL-gekrümmt $
$\qquad\qquad$ $ W_1[(-0,707)|f(-0,707)]=\underline{(-0,707|1,65)}\:\: | \:\: W_2[(0,707)|f(0,707)]=\underline{(0,707|1,65)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\:Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w_1}: f(x_{w_1})=f^\prime(x_{w_1})\cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=-0,707\\ \\ f^\prime(x_{w_1})=2,33\\ \\ f(x_{w_1})=1,65 \end{cases} $
$\qquad\qquad\qquad$ $ t_{w_1}=2,33(x+0,707)+1,65=\underline{2,33x+3,3} $
$\qquad\qquad$ $ t_{w_2}: f(x_{w_2})=f^\prime(x_{w_2})\cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=0,707\\ \\ f^\prime(x_{w_2})=-2,33\\ \\ f(x_{w_2})=1,65 \end{cases} $
$\qquad\qquad\qquad$ $ t_{w_2}=-2,33(x-0,707)+1,65=\underline{-2,33x+3,3} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\:Verhalten\:im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=0 \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $
$\qquad\:\:$ Schaubild:
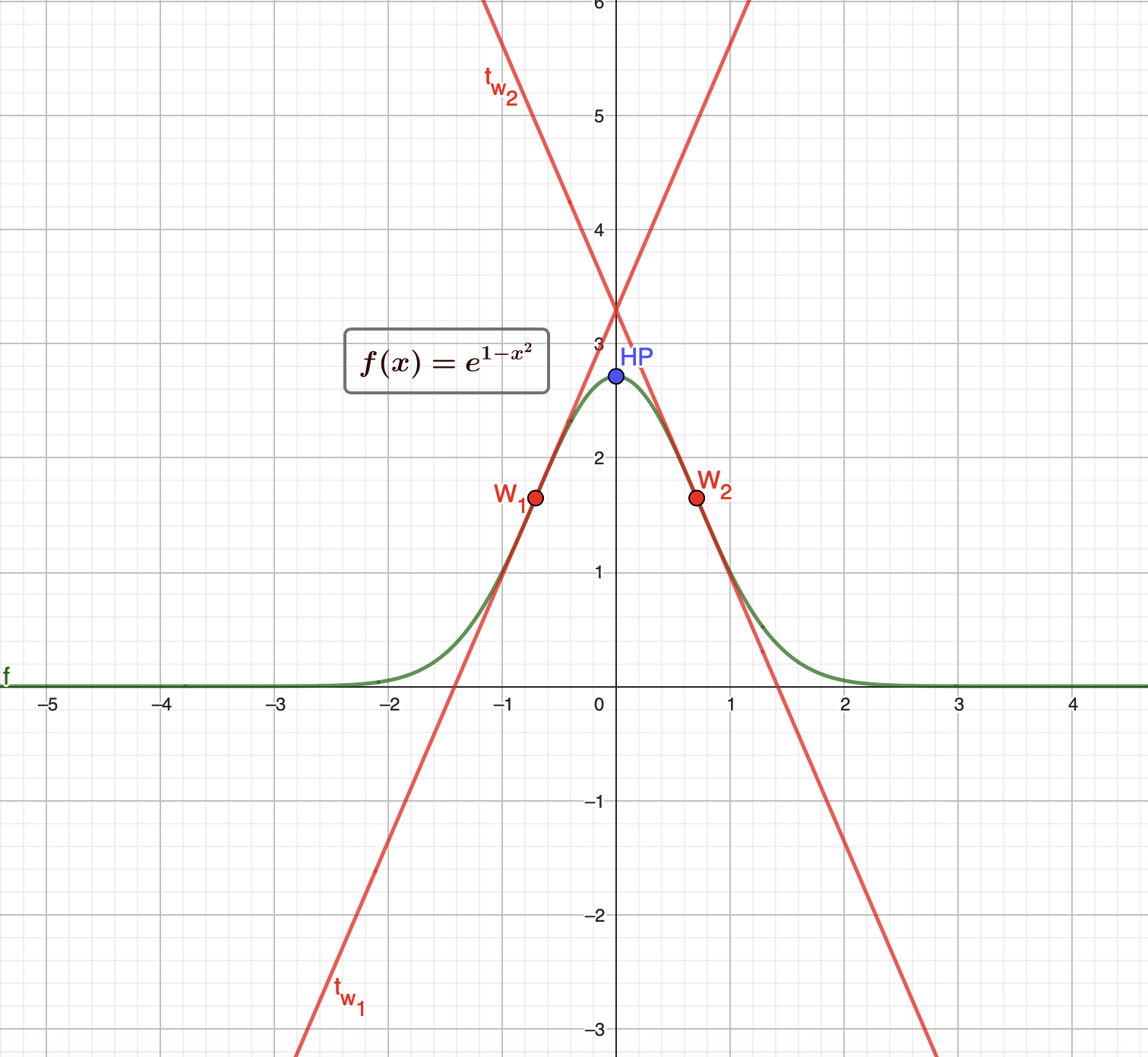
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ D_f=\forall x\in\mathbb{R}, -\infty < x < +\infty \longrightarrow D_f=]-\infty;+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ W_f=\forall y \in\mathbb{R}, 0 < y < e \longrightarrow W_f=]0;e[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $ f(x)=e^{1-x^2} $
$\qquad\qquad$ Mit Kettenregel: $ f^\prime(x)=(1-x^2)^\prime \cdot e^{1-x^2}= \underline{-2x \cdot e^{1-x^2}} $
$\qquad\:\:$ Zweite Ableitung:
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^\prime(x) \cdot v(x)+ u(x) \cdot v^\prime(x)| \begin{cases} u(x)=-2x \longrightarrow u^\prime(x)=-2\\ \\ v(x)=e^{1-x^2} \longrightarrow v^\prime(x)=-2x\cdot e^{1-x^2} \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-2\cdot e^{1-x^2}+ (-2x)\cdot (-2x) \cdot e^{1-x^2}=-2\cdot e^{1-x^2}+ 4x^2\cdot e^{1-x^2} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad$ $ =\underline{(-1+2x^2)\cdot 2e^{1-x^2}} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ Mit Produktregel und Kettenregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=u^\prime(x) \cdot v(x)+ u(x) \cdot v^\prime(x)| \begin{cases} u(x)=-1+2x^2 \longrightarrow u^\prime(x)=4x\\ \\ v(x)=2e^{1-x^2} \longrightarrow v^\prime(x)=-4x\cdot e^{1-x^2} \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=4x\cdot 2e^{1-x^2}+ (-1+2x^2)\cdot (-4x) \cdot e^{1-x^2}=4e^{1-x^2}(2x+1x-2x^3) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ =\underline{4e^{1-x^2}(3x-2x^3)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=e^{1-0^2}=e \longrightarrow \underline{S_y(0|e)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\:Nullstellen\: (Schnittpunkt\: mit\: der\: x-Achse: \longrightarrow y=f(x)=0) $
$\qquad\:\:$ $ f(x)=0 \iff e^{1-x^2}=0\:\: \textcolor{red}{n.L.}\:\: \longrightarrow keine Nullstellen $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\:Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=e^{1-(-x)^2}=e^{1-x^2}=f(x) \longrightarrow Gerade\: Funktion, Achsensymmetrie $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\:Extrempunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^\prime(x)=0, f^{\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^\prime(x)=0 \iff -2x\cdot e^{1-x^2}=0 \iff \begin{cases} -2x=0 \longrightarrow x=0\\ \\ e^{1-x^2}=0\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Es gibt ein Extrempunkt an der Stelle $x=0$
$\qquad\qquad$ $ f^{\prime\prime}(0)=[-1+2(0)^2]\cdot 2e^{1-0^2}=-2e<0 \longrightarrow Hochpunkt $
$\qquad\qquad\qquad\qquad\qquad$ $ \underline{HP[(0)|f(0)]=(0|e)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\:Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0, f^{\prime\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^{\prime\prime}(x)=0 \iff (-1+2x^2)\cdot 2e^{1-x^2}=0 $
$\qquad\qquad$ $ \iff \begin{cases} -1+2x^2=0\: \textcolor{red}{|+1}, 2x^2=1\: \textcolor{red}{|:2}, x^2=\frac{1}{2}\: \textcolor{red}{|\sqrt{…}}\: \longrightarrow \: \begin{cases} x_1=-0,707\\ \\ x_2=+0,707 \end{cases} \\ \\ 2e^{1-x^2}=0\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\qquad$ Es gibt Wendepunkte an der Stelle $x_1=-0,707$ und $x_2=+0,707$
$\qquad\qquad$ $ f^{\prime\prime\prime}(-0,707)=-9,33<0 \longrightarrow LR-gekrümmt $
$\qquad\qquad$ $ f^{\prime\prime\prime}(+0,707)=+9,33>0 \longrightarrow RL-gekrümmt $
$\qquad\qquad$ $ W_1[(-0,707)|f(-0,707)]=\underline{(-0,707|1,65)}\:\: | \:\: W_2[(0,707)|f(0,707)]=\underline{(0,707|1,65)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\:Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w_1}: f(x_{w_1})=f^\prime(x_{w_1})\cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=-0,707\\ \\ f^\prime(x_{w_1})=2,33\\ \\ f(x_{w_1})=1,65 \end{cases} $
$\qquad\qquad\qquad$ $ t_{w_1}=2,33(x+0,707)+1,65=\underline{2,33x+3,3} $
$\qquad\qquad$ $ t_{w_2}: f(x_{w_2})=f^\prime(x_{w_2})\cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=0,707\\ \\ f^\prime(x_{w_2})=-2,33\\ \\ f(x_{w_2})=1,65 \end{cases} $
$\qquad\qquad\qquad$ $ t_{w_2}=-2,33(x-0,707)+1,65=\underline{-2,33x+3,3} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\:Verhalten\:im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=0 \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $
$\qquad\:\:$ Schaubild:

$f(x)=(1-x^2)\cdot e^{- \frac{1}{2}x^2}$
Lösung
$f(x)=(1-x^2)\cdot e^{ -\frac{1}{2}x^2}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ Df=\forall x \begin{cases} (1-x^2) \in\mathbb{R}\\ \\ e^{-\frac{1}{2}x^2} \in\mathbb{R}\\ \end{cases} \longrightarrow \underline{Df=]-\infty;+\infty[} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ Wf=\forall y \in \mathbb{R}, -\infty < y < +\infty \longrightarrow \underline{Wf=]-\infty;+\infty[} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $ f(x)=(1-x^2)\cdot e^{-\frac{1}{2}x^2} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime}(x)=u^{\prime}(x) \cdot v(x) + u(x)\cdot v^{\prime}(x) | \begin{cases} u(x)=(1-x^2) \longrightarrow u^{\prime}(x)=-2x\\ \\ v(x)=e^{-\frac{1}{2}x^2} \longrightarrow v^{\prime}(x)=-x \cdot e^{-\frac{1}{2}x^2} \end{cases} $
$\qquad\qquad$ $ f^{\prime}(x)=-2x\cdot e^{-\frac{1}{2}x^2} + (1-x^2)\cdot (-x\cdot e^{-\frac{1}{2}x^2}) $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =e^{-\frac{1}{2}x^2} [-2x+(1-x^2)\cdot (-x)] $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =\underline{e^{-\frac{1}{2}x^2} (-3x+x^3)} $
$\qquad\:\:$ Zweite Ableitung:
$\qquad\qquad$ $ f^{\prime}(x)=e^{-\frac{1}{2}x^2} \cdot (-3x+x^3) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^{\prime}(x) \cdot v(x) + u(x)\cdot v^{\prime}(x) | \begin{cases} u(x)=e^{-\frac{1}{2}x^2} \longrightarrow u^{\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\\ \\ v(x)=(-3x+x^3) \longrightarrow v^{\prime}(x)=-3+3x^2 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\cdot (-3x+x^3) + e^{-\frac{1}{2}x^2}\cdot (-3+3x^2) $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =e^{-\frac{1}{2}x^2}\cdot [3x^2-x^4+(-3+3x^2)] $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =\underline{e^{-\frac{1}{2}x^2}\cdot (-x^4+6x^2-3)} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=e^{-\frac{1}{2}x^2}\cdot (-x^4+6x^2-3) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)= \begin{cases} u(x)=e^{-\frac{1}{2}x^2} \longrightarrow u^{\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\\ \\ v(x)=(-x^4+6x^2-3) \longrightarrow v^{\prime}(x)=-4x^3+12x \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\cdot (-x^4+6x^2-3) + (-4x^3+12x)\cdot e^{-\frac{1}{2}x^2} $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\:$ $ =e^{-\frac{1}{2}x^2}\cdot [x^5-6x^3+3x+(-4x^3+12x)] $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\:$ $ =\underline{e^{-\frac{1}{2}x^2}\cdot (x^5-10x^3+15x)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=(1-0^2)\cdot e^{-\frac{1}{2}0^2}=e \longrightarrow \underline{S_y(0|1)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\: (Schnittpunkt\: mit\: der\: x-Achse:\: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0 \iff (1-x^2)\cdot e^{-\frac{1}{2}x^2}=0 \Longrightarrow \begin{cases} (1-x^2)=0\:\: \textcolor{red}{|-1} \longrightarrow x=\pm1\\ \\ e^{-\frac{1}{2}x^2}=0\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Es gibt Nullstellen an der Stellen $N_1(-1|0)$ und $N_2(+1|0)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=[1-(-x)^2]\cdot e^{-\frac{1}{2}(-x)^2} =(1-x^2)\cdot e^{-\frac{1}{2}x^2} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ = f(x) \longrightarrow$ Achsensymmetrie
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkten\: untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $f^\prime(x)=0,\: f^{\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^{\prime}(x)=0 \iff e^{-\frac{1}{2}x^2}\cdot (-3x+x^3)=0 \iff \begin{cases} e^{-\frac{1}{2}x^2}=0\: \textcolor{red}{n.L.}\\ \\ (-3x+x^3)=0 \end{cases} $
$\qquad\qquad$ $ x\cdot (-3+x^2)=0 \longrightarrow \begin{cases} x=0\\ \\ (-3+x^2)=0\: \textcolor{red}{|+3} \longrightarrow x=\pm1,732 \end{cases} $
$\qquad\qquad$ Mögliche Extremspunkten bei $x_1=-1,732$, $x_2=0$ und $x_3=+1,732$
$\qquad\qquad$ Nullstellen der ersten Ableitung in zweite einsetzen:
$\qquad\qquad$ $ \begin{cases} f^{\prime\prime}(-1,732)=1,339>0 \longrightarrow ein\: Tiefpunkt\:|\: \underline{TP_1=(-1,732|-0,446)}\\ \\ f^{\prime\prime}(0)=-3<0 \longrightarrow ein\: Hochpunkt\:|\: \underline{HP=(0|1)}\\ \\ f^{\prime\prime}(+1,732)=1,339>0 \longrightarrow ein\: Tiefpunkt\:|\: \underline{TP_2=(1,732|-0,446)} \end{cases} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0,\: f^{\prime\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^{\prime\prime}(x)=0 \iff \begin{cases} e^{-\frac{1}{2}x^2}=0\: \textcolor{red}{n.L.}\\ \\ (-x^4+6x^2-3)=0\: Mit \: Substitution\: lösen: \begin{cases} x_1=-2,334\\ \\ x_2=-0,742\\ \\ x_3=0,742\\ \\ x_4=2,334 \end{cases} \end{cases} $
$\qquad\qquad$ Mögliche Wendepunkte bei:
$\qquad\qquad\qquad$ $x_{w_1}=-2,334$, $x_{w_2}=-0,742$, $x_{w_3}=0,742$ und $x_{w_4}=2,334$
$\qquad\qquad$ Nullstellen der zweite Ableitung in dritte einsetzen:
$\qquad$ $ \begin{cases} f^{\prime\prime\prime}(-2,334)=1,5>0\longrightarrow \underline{W_1(-2,334|-0,292)}, Recht-Links-Wendepunkt\\ \\ f^{\prime\prime\prime}(-0,742)=-5,52<0\longrightarrow \underline{W_2(-0,742|0,341)}, Links-Recht-Wendepunkt\\ \\ f^{\prime\prime\prime}(0,742)=5,52>0\longrightarrow \underline{W_3(0,742|0,341)}, Recht-Links-Wendepunkt\\ \\ f^{\prime\prime\prime}(2,334)=-1,5<0\longrightarrow \underline{W_4(2,334|-0,292)}, Links-Recht-Wendepunkt \end{cases} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w_1}: f^{\prime}(x_{w_1})\cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=-2,334\\ \\ f^{\prime}(x_{w_1})=-0,375\\ \\ f(x_{w_1})=-0,292 \end{cases} $
$\qquad\qquad$ $ t_{w_1}=-0,375(x+2,334)-0,292=\underline{-0,375x-1,167} $
$\qquad\qquad$ $ t_{w_2}: f^{\prime}(x_{w_2})\cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=-0,742\\ \\ f^{\prime}(x_{w_2})=1,38\\ \\ f(x_{w_2})=0,341 \end{cases} $
$\qquad\qquad$ $ t_{w_2}=1,38(x+0,742)+0,341=\underline{1,38x+1,36} $
$\qquad\qquad$ $ t_{w_3}: f^{\prime}(x_{w_3})\cdot (x-x_{w_3})+f(x_{w_3}) $ mit $ \begin{cases} x_{w_3}=0,742\\ \\ f^{\prime}(x_{w_3})=-1,38\\ \\ f(x_{w_3})=0,341 \end{cases} $
$\qquad\qquad$ $ t_{w_3}=-1,38(x-0,742)+0,341=\underline{-1,38x+1,36} $
$\qquad\qquad$ $ t_{w_4}: f^{\prime}(x_{w_4})\cdot (x-x_{w_4})+f(x_{w_4}) $ mit $ \begin{cases} x_{w_4}=2,334\\ \\ f^{\prime}(x_{w_4})=0,375\\ \\ f(x_{w_4})=-0,292 \end{cases} $
$\qquad\qquad$ $ t_{w_4}=0,375(x-2,334)-0,292=\underline{0,375x-1,167} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=0 \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $
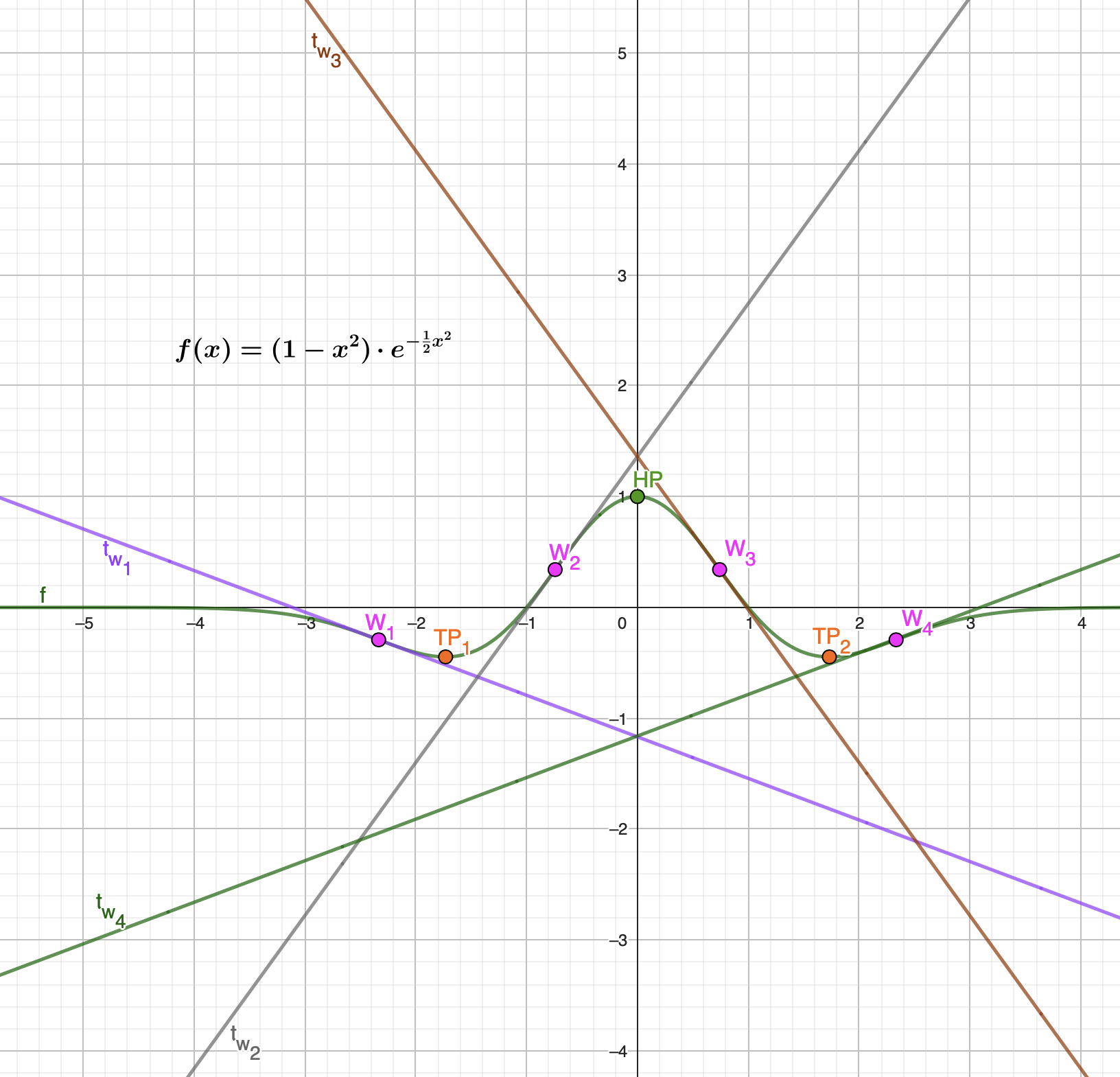
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ Df=\forall x \begin{cases} (1-x^2) \in\mathbb{R}\\ \\ e^{-\frac{1}{2}x^2} \in\mathbb{R}\\ \end{cases} \longrightarrow \underline{Df=]-\infty;+\infty[} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ Wf=\forall y \in \mathbb{R}, -\infty < y < +\infty \longrightarrow \underline{Wf=]-\infty;+\infty[} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $ f(x)=(1-x^2)\cdot e^{-\frac{1}{2}x^2} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime}(x)=u^{\prime}(x) \cdot v(x) + u(x)\cdot v^{\prime}(x) | \begin{cases} u(x)=(1-x^2) \longrightarrow u^{\prime}(x)=-2x\\ \\ v(x)=e^{-\frac{1}{2}x^2} \longrightarrow v^{\prime}(x)=-x \cdot e^{-\frac{1}{2}x^2} \end{cases} $
$\qquad\qquad$ $ f^{\prime}(x)=-2x\cdot e^{-\frac{1}{2}x^2} + (1-x^2)\cdot (-x\cdot e^{-\frac{1}{2}x^2}) $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =e^{-\frac{1}{2}x^2} [-2x+(1-x^2)\cdot (-x)] $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =\underline{e^{-\frac{1}{2}x^2} (-3x+x^3)} $
$\qquad\:\:$ Zweite Ableitung:
$\qquad\qquad$ $ f^{\prime}(x)=e^{-\frac{1}{2}x^2} \cdot (-3x+x^3) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^{\prime}(x) \cdot v(x) + u(x)\cdot v^{\prime}(x) | \begin{cases} u(x)=e^{-\frac{1}{2}x^2} \longrightarrow u^{\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\\ \\ v(x)=(-3x+x^3) \longrightarrow v^{\prime}(x)=-3+3x^2 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\cdot (-3x+x^3) + e^{-\frac{1}{2}x^2}\cdot (-3+3x^2) $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =e^{-\frac{1}{2}x^2}\cdot [3x^2-x^4+(-3+3x^2)] $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:$ $ =\underline{e^{-\frac{1}{2}x^2}\cdot (-x^4+6x^2-3)} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=e^{-\frac{1}{2}x^2}\cdot (-x^4+6x^2-3) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)= \begin{cases} u(x)=e^{-\frac{1}{2}x^2} \longrightarrow u^{\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\\ \\ v(x)=(-x^4+6x^2-3) \longrightarrow v^{\prime}(x)=-4x^3+12x \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=-x\cdot e^{-\frac{1}{2}x^2}\cdot (-x^4+6x^2-3) + (-4x^3+12x)\cdot e^{-\frac{1}{2}x^2} $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\:$ $ =e^{-\frac{1}{2}x^2}\cdot [x^5-6x^3+3x+(-4x^3+12x)] $
$\qquad\qquad\:\:\:\:\:\:\:\:\:\:\:\:$ $ =\underline{e^{-\frac{1}{2}x^2}\cdot (x^5-10x^3+15x)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=(1-0^2)\cdot e^{-\frac{1}{2}0^2}=e \longrightarrow \underline{S_y(0|1)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\: (Schnittpunkt\: mit\: der\: x-Achse:\: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0 \iff (1-x^2)\cdot e^{-\frac{1}{2}x^2}=0 \Longrightarrow \begin{cases} (1-x^2)=0\:\: \textcolor{red}{|-1} \longrightarrow x=\pm1\\ \\ e^{-\frac{1}{2}x^2}=0\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Es gibt Nullstellen an der Stellen $N_1(-1|0)$ und $N_2(+1|0)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=[1-(-x)^2]\cdot e^{-\frac{1}{2}(-x)^2} =(1-x^2)\cdot e^{-\frac{1}{2}x^2} $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ = f(x) \longrightarrow$ Achsensymmetrie
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkten\: untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $f^\prime(x)=0,\: f^{\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^{\prime}(x)=0 \iff e^{-\frac{1}{2}x^2}\cdot (-3x+x^3)=0 \iff \begin{cases} e^{-\frac{1}{2}x^2}=0\: \textcolor{red}{n.L.}\\ \\ (-3x+x^3)=0 \end{cases} $
$\qquad\qquad$ $ x\cdot (-3+x^2)=0 \longrightarrow \begin{cases} x=0\\ \\ (-3+x^2)=0\: \textcolor{red}{|+3} \longrightarrow x=\pm1,732 \end{cases} $
$\qquad\qquad$ Mögliche Extremspunkten bei $x_1=-1,732$, $x_2=0$ und $x_3=+1,732$
$\qquad\qquad$ Nullstellen der ersten Ableitung in zweite einsetzen:
$\qquad\qquad$ $ \begin{cases} f^{\prime\prime}(-1,732)=1,339>0 \longrightarrow ein\: Tiefpunkt\:|\: \underline{TP_1=(-1,732|-0,446)}\\ \\ f^{\prime\prime}(0)=-3<0 \longrightarrow ein\: Hochpunkt\:|\: \underline{HP=(0|1)}\\ \\ f^{\prime\prime}(+1,732)=1,339>0 \longrightarrow ein\: Tiefpunkt\:|\: \underline{TP_2=(1,732|-0,446)} \end{cases} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0,\: f^{\prime\prime\prime}(x)\neq0$
$\qquad\qquad$ $ f^{\prime\prime}(x)=0 \iff \begin{cases} e^{-\frac{1}{2}x^2}=0\: \textcolor{red}{n.L.}\\ \\ (-x^4+6x^2-3)=0\: Mit \: Substitution\: lösen: \begin{cases} x_1=-2,334\\ \\ x_2=-0,742\\ \\ x_3=0,742\\ \\ x_4=2,334 \end{cases} \end{cases} $
$\qquad\qquad$ Mögliche Wendepunkte bei:
$\qquad\qquad\qquad$ $x_{w_1}=-2,334$, $x_{w_2}=-0,742$, $x_{w_3}=0,742$ und $x_{w_4}=2,334$
$\qquad\qquad$ Nullstellen der zweite Ableitung in dritte einsetzen:
$\qquad$ $ \begin{cases} f^{\prime\prime\prime}(-2,334)=1,5>0\longrightarrow \underline{W_1(-2,334|-0,292)}, Recht-Links-Wendepunkt\\ \\ f^{\prime\prime\prime}(-0,742)=-5,52<0\longrightarrow \underline{W_2(-0,742|0,341)}, Links-Recht-Wendepunkt\\ \\ f^{\prime\prime\prime}(0,742)=5,52>0\longrightarrow \underline{W_3(0,742|0,341)}, Recht-Links-Wendepunkt\\ \\ f^{\prime\prime\prime}(2,334)=-1,5<0\longrightarrow \underline{W_4(2,334|-0,292)}, Links-Recht-Wendepunkt \end{cases} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w_1}: f^{\prime}(x_{w_1})\cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=-2,334\\ \\ f^{\prime}(x_{w_1})=-0,375\\ \\ f(x_{w_1})=-0,292 \end{cases} $
$\qquad\qquad$ $ t_{w_1}=-0,375(x+2,334)-0,292=\underline{-0,375x-1,167} $
$\qquad\qquad$ $ t_{w_2}: f^{\prime}(x_{w_2})\cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=-0,742\\ \\ f^{\prime}(x_{w_2})=1,38\\ \\ f(x_{w_2})=0,341 \end{cases} $
$\qquad\qquad$ $ t_{w_2}=1,38(x+0,742)+0,341=\underline{1,38x+1,36} $
$\qquad\qquad$ $ t_{w_3}: f^{\prime}(x_{w_3})\cdot (x-x_{w_3})+f(x_{w_3}) $ mit $ \begin{cases} x_{w_3}=0,742\\ \\ f^{\prime}(x_{w_3})=-1,38\\ \\ f(x_{w_3})=0,341 \end{cases} $
$\qquad\qquad$ $ t_{w_3}=-1,38(x-0,742)+0,341=\underline{-1,38x+1,36} $
$\qquad\qquad$ $ t_{w_4}: f^{\prime}(x_{w_4})\cdot (x-x_{w_4})+f(x_{w_4}) $ mit $ \begin{cases} x_{w_4}=2,334\\ \\ f^{\prime}(x_{w_4})=0,375\\ \\ f(x_{w_4})=-0,292 \end{cases} $
$\qquad\qquad$ $ t_{w_4}=0,375(x-2,334)-0,292=\underline{0,375x-1,167} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=0 \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $

$f(x)=e^{-3x}\cdot (2x-4)$
Lösung
$f(x)=e^{-3x}\cdot (2x-4)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ Df=\forall x \begin{cases} e^{-3x} \in \mathbb{R}\\ \\ (2x-4) \in \mathbb{R} \end{cases} \:\: \longrightarrow \underline { Df= ]-\infty;\infty[ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ Wf=\forall y \in \mathbb{R}$, $-\infty < y \leq \frac{2}{3e^7} \longrightarrow \underline {Wf=]-\infty;\frac{2}{3e^7}]} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $f(x)=e^{-3x}\cdot (2x-4)$
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)= u^\prime(x)\cdot v(x)+ u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=e^{-3x} \longrightarrow u^\prime(x)=-3e^{-3x}\\ \\ v(x)=(2x-4) \longrightarrow v^\prime(x)=2 \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=-3e^{-3x}\cdot (2x-4)+e^{-3x}\cdot 2 $
$\qquad\qquad\qquad\:$ $ =e^{-3x}\cdot [-3(2x-4)+2] $
$\qquad\qquad\qquad\:$ $ =\underline{e^{-3x}\cdot (-6x+14)} $
$\qquad\:\:$ zweite Ableitung:
$\qquad\qquad$ $f^\prime(x)=e^{-3x}\cdot (-6x+14)$
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)= u^\prime(x)\cdot v(x)+ u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=e^{-3x} \longrightarrow u^\prime(x)=-3e^{-3x}\\ \\ v(x)=(-6x+14) \longrightarrow v^\prime(x)=-6 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-3e^{-3x}\cdot (-6x+14)+e^{-3x}\cdot (-6) $
$\qquad\qquad\qquad\:\:\:$ $ =e^{-3x}\cdot [-3(-6x+14)+(-6)] $
$\qquad\qquad\qquad\:\:\:$ $ =\underline{e^{-3x}\cdot (18x-48)} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ $f^{\prime\prime}(x)=e^{-3x}\cdot (18x-48)$
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)= u^\prime(x)\cdot v(x)+ u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=e^{-3x} \longrightarrow u^\prime(x)=-3e^{-3x}\\ \\ v(x)=(18x-48) \longrightarrow v^\prime(x)=18 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=-3e^{-3x}\cdot (18x-48)+e^{-3x}\cdot (18) $
$\qquad\qquad\qquad\:\:\:$ $ =e^{-3x}\cdot [-3(18x-48)+(18)] $
$\qquad\qquad\qquad\:\:\:$ $ =\underline{e^{-3x}\cdot (-54x+162)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=e^{-3(0)}\cdot [2(0)-4]=-4 \longrightarrow \underline{S_y(0|-4)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\: (Schnittpunkt\: mit\: der\: x-Achse:\: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0 \iff e^{-3x}\cdot (2x-4)=0 \Longrightarrow \begin{cases} e^{-3x}=0\: \textcolor{red}{n.L.}\\ \\ (2x-4)=0\: \textcolor{red}{|(+4),\: (:2)} \longrightarrow x_0=2 \end{cases} $
$\qquad\:\:$ Es gibt eine Nullstelle an der Stelle $\underline{N_0(2|0)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=e^{-3(-x)}\cdot [2(-x)-4]=e^{3x}\cdot (-2x-4) $
$\qquad\qquad\:\:\:\:\:\:$ $ \ne f(x) \longrightarrow$ kein Achsensymmetrie zur y-Achse
$\qquad\qquad\:\:\:\:\:\:$ $ \ne -f(x) \longrightarrow$ kein Punktsymmetrie zum Ursprung
$\qquad\:\:$ $f(x)= e^{-3x}\cdot (2x-4)$ ist weder achsensymmetrisch noch punktsymmetrisch.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkten\: Untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $ f^\prime(x)=0, f^{\prime\prime}(x)\ne0 $
$\qquad\qquad$ $ f^\prime(x)=0 \iff e^{-3x}\cdot (-6x+14)=0 \iff \begin{cases} e^{-3x}=0\: \textcolor{red}{n.L.}\\ \\ (-6x+14)=0\: \textcolor{red}{|(-14)} \longrightarrow x_1=\frac{7}{3} \end{cases} $
$\qquad\qquad$ Möglicher Extremspunkt bei $x_1=\frac{7}{3}$
$\qquad\qquad$ Nullstelle der ersten Ableitung in zweite einsetzen:
$\qquad\qquad$ $ f^{\prime\prime}(\frac{7}{3})= e^{-3(\frac{7}{3})}\cdot [18(\frac{7}{3})-48]=-0,005<0 \longrightarrow Hochpunkt $
$\qquad\qquad$ Der Hochpunkt beträgt: $ HP[\frac{7}{3}|f(\frac{7}{3})]=\underline{(\frac{7}{3}|\frac{2}{3e^7})} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkten\: Untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0$, $f^{\prime\prime\prime}(x)\ne0$
$\qquad\qquad$ $ f^{\prime\prime}(x)=0 \iff \begin{cases} e^{-3x}=0\: \textcolor{red}{n.L.}\\ \\ (18x-48)=0\: \textcolor{red}{|(+48)} \longrightarrow x_2=\frac{8}{3} \end{cases} $
$\qquad\qquad$ Möglicher Wendepunkt bei $x_w=\frac{8}{3}$
$\qquad\qquad$ Nullstelle der zweiten Ableitung in dritte einsetzen:
$\qquad\qquad$ $ f^{\prime\prime\prime}(\frac{8}{3})=00060>0 \longrightarrow Recht-Links-Wendepunkt $
$\qquad\qquad$ Der Wendepunkt beträgt: $W[\frac{8}{3}|f(\frac{8}{3})]=\underline{(\frac{8}{3}|\frac{4}{3e^8})}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w}:f^\prime(x_w)\cdot (x-x_w)+f(x_w) $ mit $ \begin{cases} x_w=\frac{8}{3}\\ \\ f^\prime(\frac{8}{3})=-\frac{2}{e^8}\\ \\ f(\frac{8}{3})=\frac{4}{3e^8} \end{cases} $
$\qquad\qquad$ $ t_{w}=-\frac{2}{e^8}(x-\frac{8}{3})+ \frac{4}{3e^8}=\underline{-\frac{2}{e^8}x+\frac{20}{3e^8}} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=-\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $
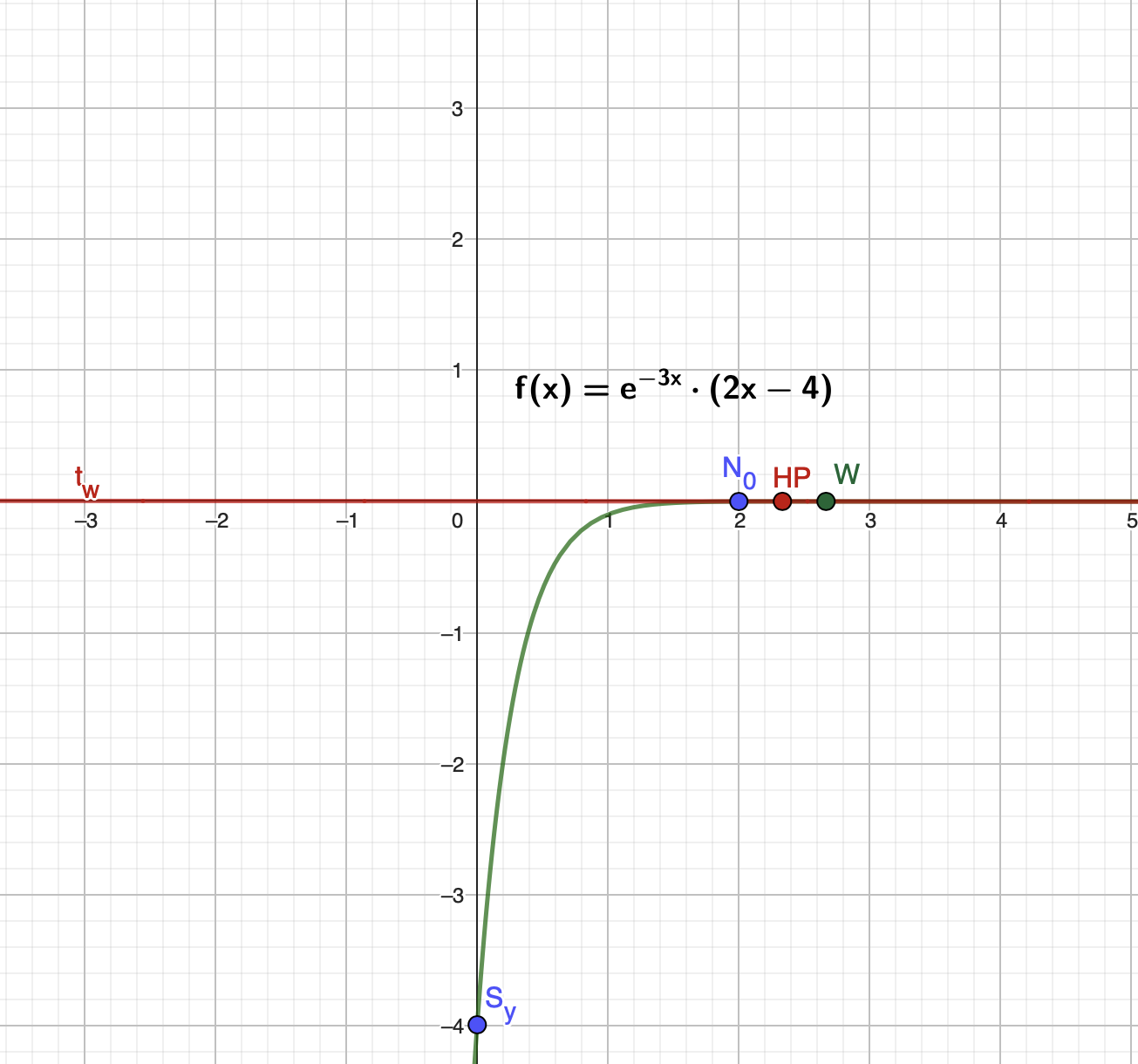
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ Df=\forall x \begin{cases} e^{-3x} \in \mathbb{R}\\ \\ (2x-4) \in \mathbb{R} \end{cases} \:\: \longrightarrow \underline { Df= ]-\infty;\infty[ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ Wf=\forall y \in \mathbb{R}$, $-\infty < y \leq \frac{2}{3e^7} \longrightarrow \underline {Wf=]-\infty;\frac{2}{3e^7}]} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $f(x)=e^{-3x}\cdot (2x-4)$
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)= u^\prime(x)\cdot v(x)+ u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=e^{-3x} \longrightarrow u^\prime(x)=-3e^{-3x}\\ \\ v(x)=(2x-4) \longrightarrow v^\prime(x)=2 \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=-3e^{-3x}\cdot (2x-4)+e^{-3x}\cdot 2 $
$\qquad\qquad\qquad\:$ $ =e^{-3x}\cdot [-3(2x-4)+2] $
$\qquad\qquad\qquad\:$ $ =\underline{e^{-3x}\cdot (-6x+14)} $
$\qquad\:\:$ zweite Ableitung:
$\qquad\qquad$ $f^\prime(x)=e^{-3x}\cdot (-6x+14)$
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)= u^\prime(x)\cdot v(x)+ u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=e^{-3x} \longrightarrow u^\prime(x)=-3e^{-3x}\\ \\ v(x)=(-6x+14) \longrightarrow v^\prime(x)=-6 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-3e^{-3x}\cdot (-6x+14)+e^{-3x}\cdot (-6) $
$\qquad\qquad\qquad\:\:\:$ $ =e^{-3x}\cdot [-3(-6x+14)+(-6)] $
$\qquad\qquad\qquad\:\:\:$ $ =\underline{e^{-3x}\cdot (18x-48)} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ $f^{\prime\prime}(x)=e^{-3x}\cdot (18x-48)$
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)= u^\prime(x)\cdot v(x)+ u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=e^{-3x} \longrightarrow u^\prime(x)=-3e^{-3x}\\ \\ v(x)=(18x-48) \longrightarrow v^\prime(x)=18 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=-3e^{-3x}\cdot (18x-48)+e^{-3x}\cdot (18) $
$\qquad\qquad\qquad\:\:\:$ $ =e^{-3x}\cdot [-3(18x-48)+(18)] $
$\qquad\qquad\qquad\:\:\:$ $ =\underline{e^{-3x}\cdot (-54x+162)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=e^{-3(0)}\cdot [2(0)-4]=-4 \longrightarrow \underline{S_y(0|-4)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\: (Schnittpunkt\: mit\: der\: x-Achse:\: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0 \iff e^{-3x}\cdot (2x-4)=0 \Longrightarrow \begin{cases} e^{-3x}=0\: \textcolor{red}{n.L.}\\ \\ (2x-4)=0\: \textcolor{red}{|(+4),\: (:2)} \longrightarrow x_0=2 \end{cases} $
$\qquad\:\:$ Es gibt eine Nullstelle an der Stelle $\underline{N_0(2|0)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=e^{-3(-x)}\cdot [2(-x)-4]=e^{3x}\cdot (-2x-4) $
$\qquad\qquad\:\:\:\:\:\:$ $ \ne f(x) \longrightarrow$ kein Achsensymmetrie zur y-Achse
$\qquad\qquad\:\:\:\:\:\:$ $ \ne -f(x) \longrightarrow$ kein Punktsymmetrie zum Ursprung
$\qquad\:\:$ $f(x)= e^{-3x}\cdot (2x-4)$ ist weder achsensymmetrisch noch punktsymmetrisch.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkten\: Untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $ f^\prime(x)=0, f^{\prime\prime}(x)\ne0 $
$\qquad\qquad$ $ f^\prime(x)=0 \iff e^{-3x}\cdot (-6x+14)=0 \iff \begin{cases} e^{-3x}=0\: \textcolor{red}{n.L.}\\ \\ (-6x+14)=0\: \textcolor{red}{|(-14)} \longrightarrow x_1=\frac{7}{3} \end{cases} $
$\qquad\qquad$ Möglicher Extremspunkt bei $x_1=\frac{7}{3}$
$\qquad\qquad$ Nullstelle der ersten Ableitung in zweite einsetzen:
$\qquad\qquad$ $ f^{\prime\prime}(\frac{7}{3})= e^{-3(\frac{7}{3})}\cdot [18(\frac{7}{3})-48]=-0,005<0 \longrightarrow Hochpunkt $
$\qquad\qquad$ Der Hochpunkt beträgt: $ HP[\frac{7}{3}|f(\frac{7}{3})]=\underline{(\frac{7}{3}|\frac{2}{3e^7})} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkten\: Untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}(x)=0$, $f^{\prime\prime\prime}(x)\ne0$
$\qquad\qquad$ $ f^{\prime\prime}(x)=0 \iff \begin{cases} e^{-3x}=0\: \textcolor{red}{n.L.}\\ \\ (18x-48)=0\: \textcolor{red}{|(+48)} \longrightarrow x_2=\frac{8}{3} \end{cases} $
$\qquad\qquad$ Möglicher Wendepunkt bei $x_w=\frac{8}{3}$
$\qquad\qquad$ Nullstelle der zweiten Ableitung in dritte einsetzen:
$\qquad\qquad$ $ f^{\prime\prime\prime}(\frac{8}{3})=00060>0 \longrightarrow Recht-Links-Wendepunkt $
$\qquad\qquad$ Der Wendepunkt beträgt: $W[\frac{8}{3}|f(\frac{8}{3})]=\underline{(\frac{8}{3}|\frac{4}{3e^8})}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_{w}:f^\prime(x_w)\cdot (x-x_w)+f(x_w) $ mit $ \begin{cases} x_w=\frac{8}{3}\\ \\ f^\prime(\frac{8}{3})=-\frac{2}{e^8}\\ \\ f(\frac{8}{3})=\frac{4}{3e^8} \end{cases} $
$\qquad\qquad$ $ t_{w}=-\frac{2}{e^8}(x-\frac{8}{3})+ \frac{4}{3e^8}=\underline{-\frac{2}{e^8}x+\frac{20}{3e^8}} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=-\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $

$f(x)=\frac{1}{2}e^{-2x}\cdot (1+x)$
Lösung
$f(x)=\frac{1}{2}e^{-2x}\cdot (1+x)$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ Df=\forall x \begin{cases} \frac{1}{2}e^{-2x}\: \in \mathbb{R}\\ \\ (1+x)\: \in \mathbb{R} \end{cases} \longrightarrow Df=]-\infty;+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ Wf=\forall y \in \mathbb{R}, -\infty < y \leq \frac{e}{4} \longrightarrow Wf=]-\infty;\frac{e}{4}] $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $ f(x)=\frac{1}{2}e^{-2x}\cdot (1+x) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=\frac{1}{2}e^{-2x} \longrightarrow u^\prime(x)=-e^{-2x}\\ \\ v(x)=(1+x) \longrightarrow v^\prime(x)=1 \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=-e^{-2x}\cdot (1+x)+\frac{1}{2}e^{-2x}\cdot (1) $
$\qquad\qquad\qquad\:$ $ =e^{-2x}[-(1+x)+\frac{1}{2}] $
$\qquad\qquad\qquad\:$ $ =\underline{-e^{-2x}(\frac{1}{2}+x)} $
$\qquad\:\:$ Zweite Ableitung:
$\qquad\qquad$ $ f^\prime(x)=-e^{-2x}(\frac{1}{2}+x) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=-e^{-2x} \longrightarrow u^\prime(x)=2e^{-2x}\\ \\ v(x)=(\frac{1}{2}+x) \longrightarrow v^\prime(x)=1 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=[2e^{-2x}\cdot (\frac{1}{2}+x)+(-e^{-2x})\cdot (1)] $
$\qquad\qquad\qquad\:\:$ $ =e^{-2x}[2\cdot(\frac{1}{2}+x)+(-1)] $
$\qquad\qquad\qquad\:\:$ $ =\underline{2x\cdot e^{-2x}} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ $ f^{\prime\prime}(x)=2x\cdot e^{-2x} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=2x \longrightarrow u^\prime(x)=2\\ \\ v(x)=e^{-2x} \longrightarrow v^\prime(x)=-2e^{-2x} \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=[2\cdot e^{-2x}+2x\cdot (-2e^{-2x})] $
$\qquad\qquad\qquad\:\:$ $ =2e^{-2x}\cdot (1-2x) $
$\qquad\qquad\qquad\:\:$ $ =\underline{2e^{-2x}\cdot (1-2x)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkte\: mit\: der\: y-Achse: S_y[0|f(0)] $
$\qquad\:\:$ $ f(0)=\frac{1}{2}e^{-2(0)}\cdot [1+(0)]=\frac{1}{2} \longrightarrow \underline{S_y(0|\frac{1}{2})} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\: (Schnittpunkte\: mit\: der\: x-Achse: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0 \iff \frac{1}{2} e^{-2x} \cdot (1+x)=0 \Longrightarrow \begin{cases} \frac{1}{2}e^{-2x}=0\: \textcolor{red}{n.L.}\\ \\ (1+x)=0\: \textcolor{red}{|\: -(1)} \longrightarrow x_0=-1 \end{cases} $
$\qquad\:\:$ Es gibt eine Nullstelle an der Stelle $\underline{N_0=(-1|0)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=\frac{1}{2}e^{-2(-x)}\cdot [1+(-x)] =\frac{1}{2}e^{2x}\cdot (1-x) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ \ne f(x) \longrightarrow$ keine Achsensymmetrie
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ \ne -f(x) \longrightarrow$ keine Punktsymmetrie
$\qquad\:\:$ $ f(x)=\frac{1}{2}e^{-2x}\cdot (1+x)$ ist weder achsensymmetrisch noch punktsymmetrisch.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkte\: untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $f^\prime(x)=0,\: f^{\prime\prime}(x)\ne0$
$\qquad\:\:$ $ f^\prime(x)=0 \iff -e^{-2x}\cdot (\frac{1}{2}+x)=0 \iff \begin{cases} -e^{-2x}=0\: \textcolor{red}{n.L.}\\ \\ (\frac{1}{2}+x)=0 \textcolor{red}{|(-\frac{1}{2})} \longrightarrow x_1=-\frac{1}{2} \end{cases} $
$\qquad\:\:$ Möglicher Extremspunkt bei $x_1=-\frac{1}{2}$
$\qquad\:\:$ Nullstelle der ersten Ableitung in zweite einsetzen:
$\qquad\:\:$ $ f^{\prime\prime}(-\frac{1}{2})=2(-\frac{1}{2})\cdot e^{-2(-\frac{1}{2})}=-e<0 \longrightarrow Hochpunkt $
$\qquad\:\:$ Der Hochpunkt beträgt: $\underline{HP(-0,5|0,68)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}=0, f^{\prime\prime\prime}\ne0$
$\qquad\:\:$ $ f^{\prime\prime}=0 \iff \begin{cases} 2x=0 \longrightarrow x_2=0\\ \\ e^{-2x}=0\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Möglicher Wendepunkt bei $x_w=0$
$\qquad\:\:$ Nullstelle der zweiten Ableitung in dritte einsetzen:
$\qquad\:\:$ $ f^{\prime\prime\prime}(0)=2e^{-2(0)}\cdot [1-2(0)]=2>0 \longrightarrow Recht-Links-Wendepunkt $
$\qquad\:\:$ Der Wendepunkt beträgt: $\underline{W(0|0,5)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_w: f^\prime(x_w)\cdot (x-x_w)+f(x_w) $ mit $ \begin{cases} x_w=0\\ \\ f^\prime(0)=-\frac{1}{2}\\ \\ f(0)=\frac{1}{2} \end{cases} $
$\qquad\qquad$ $ t_w=-\frac{1}{2}(x-0)+\frac{1}{2}=\underline{-\frac{1}{2}x+\frac{1}{2}} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=-\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $
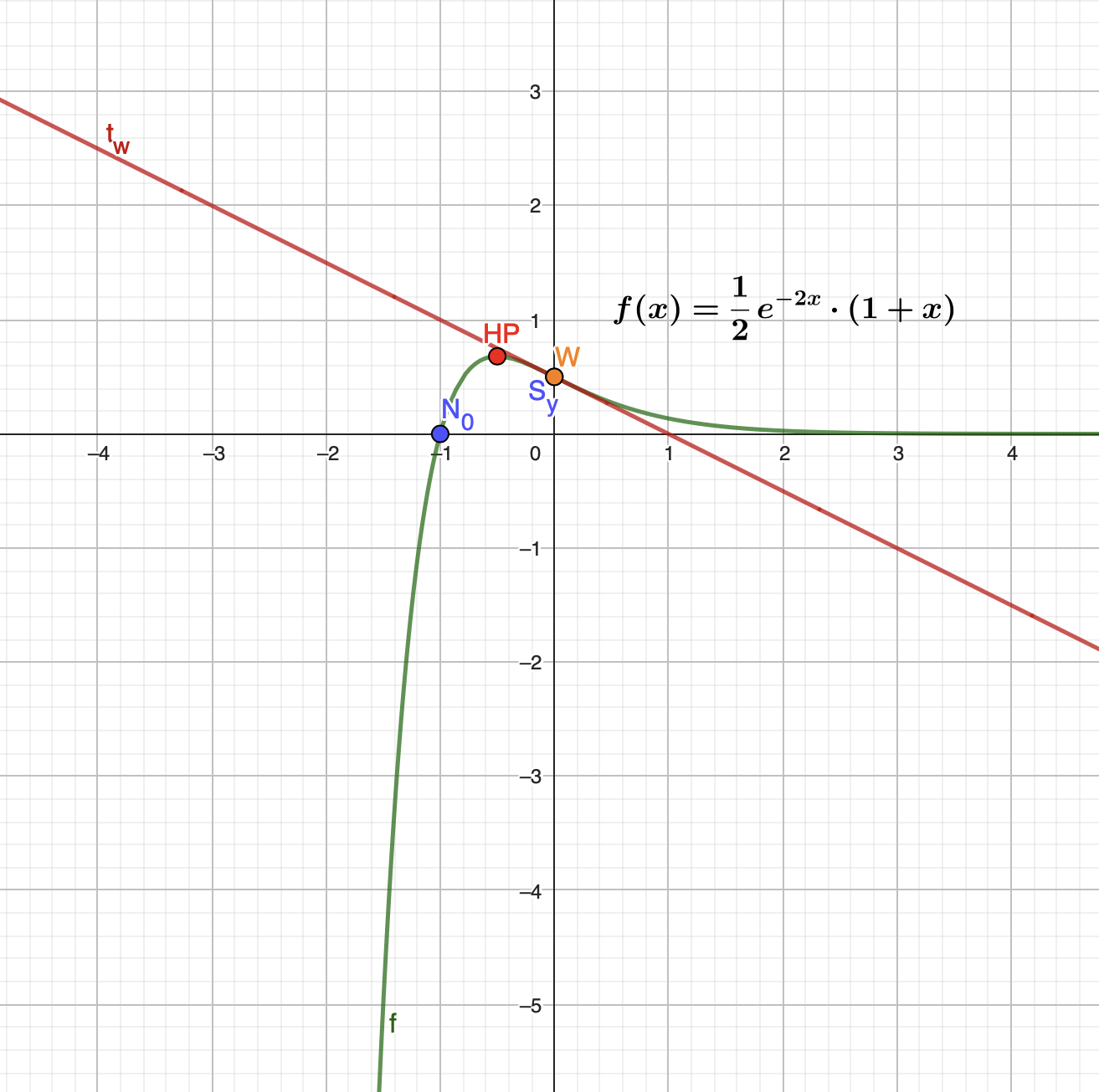
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ Df=\forall x \begin{cases} \frac{1}{2}e^{-2x}\: \in \mathbb{R}\\ \\ (1+x)\: \in \mathbb{R} \end{cases} \longrightarrow Df=]-\infty;+\infty[ $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertebereich\: ermitteln $
$\qquad\:\:$ $ Wf=\forall y \in \mathbb{R}, -\infty < y \leq \frac{e}{4} \longrightarrow Wf=]-\infty;\frac{e}{4}] $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung:
$\qquad\qquad$ $ f(x)=\frac{1}{2}e^{-2x}\cdot (1+x) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=\frac{1}{2}e^{-2x} \longrightarrow u^\prime(x)=-e^{-2x}\\ \\ v(x)=(1+x) \longrightarrow v^\prime(x)=1 \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=-e^{-2x}\cdot (1+x)+\frac{1}{2}e^{-2x}\cdot (1) $
$\qquad\qquad\qquad\:$ $ =e^{-2x}[-(1+x)+\frac{1}{2}] $
$\qquad\qquad\qquad\:$ $ =\underline{-e^{-2x}(\frac{1}{2}+x)} $
$\qquad\:\:$ Zweite Ableitung:
$\qquad\qquad$ $ f^\prime(x)=-e^{-2x}(\frac{1}{2}+x) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=-e^{-2x} \longrightarrow u^\prime(x)=2e^{-2x}\\ \\ v(x)=(\frac{1}{2}+x) \longrightarrow v^\prime(x)=1 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=[2e^{-2x}\cdot (\frac{1}{2}+x)+(-e^{-2x})\cdot (1)] $
$\qquad\qquad\qquad\:\:$ $ =e^{-2x}[2\cdot(\frac{1}{2}+x)+(-1)] $
$\qquad\qquad\qquad\:\:$ $ =\underline{2x\cdot e^{-2x}} $
$\qquad\:\:$ Dritte Ableitung:
$\qquad\qquad$ $ f^{\prime\prime}(x)=2x\cdot e^{-2x} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:|\: \begin{cases} u(x)=2x \longrightarrow u^\prime(x)=2\\ \\ v(x)=e^{-2x} \longrightarrow v^\prime(x)=-2e^{-2x} \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=[2\cdot e^{-2x}+2x\cdot (-2e^{-2x})] $
$\qquad\qquad\qquad\:\:$ $ =2e^{-2x}\cdot (1-2x) $
$\qquad\qquad\qquad\:\:$ $ =\underline{2e^{-2x}\cdot (1-2x)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkte\: mit\: der\: y-Achse: S_y[0|f(0)] $
$\qquad\:\:$ $ f(0)=\frac{1}{2}e^{-2(0)}\cdot [1+(0)]=\frac{1}{2} \longrightarrow \underline{S_y(0|\frac{1}{2})} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen\: (Schnittpunkte\: mit\: der\: x-Achse: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0 \iff \frac{1}{2} e^{-2x} \cdot (1+x)=0 \Longrightarrow \begin{cases} \frac{1}{2}e^{-2x}=0\: \textcolor{red}{n.L.}\\ \\ (1+x)=0\: \textcolor{red}{|\: -(1)} \longrightarrow x_0=-1 \end{cases} $
$\qquad\:\:$ Es gibt eine Nullstelle an der Stelle $\underline{N_0=(-1|0)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=\frac{1}{2}e^{-2(-x)}\cdot [1+(-x)] =\frac{1}{2}e^{2x}\cdot (1-x) $
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ \ne f(x) \longrightarrow$ keine Achsensymmetrie
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:\:\:\:\:\:\:$ $ \ne -f(x) \longrightarrow$ keine Punktsymmetrie
$\qquad\:\:$ $ f(x)=\frac{1}{2}e^{-2x}\cdot (1+x)$ ist weder achsensymmetrisch noch punktsymmetrisch.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\: Extrempunkte\: untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $f^\prime(x)=0,\: f^{\prime\prime}(x)\ne0$
$\qquad\:\:$ $ f^\prime(x)=0 \iff -e^{-2x}\cdot (\frac{1}{2}+x)=0 \iff \begin{cases} -e^{-2x}=0\: \textcolor{red}{n.L.}\\ \\ (\frac{1}{2}+x)=0 \textcolor{red}{|(-\frac{1}{2})} \longrightarrow x_1=-\frac{1}{2} \end{cases} $
$\qquad\:\:$ Möglicher Extremspunkt bei $x_1=-\frac{1}{2}$
$\qquad\:\:$ Nullstelle der ersten Ableitung in zweite einsetzen:
$\qquad\:\:$ $ f^{\prime\prime}(-\frac{1}{2})=2(-\frac{1}{2})\cdot e^{-2(-\frac{1}{2})}=-e<0 \longrightarrow Hochpunkt $
$\qquad\:\:$ Der Hochpunkt beträgt: $\underline{HP(-0,5|0,68)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\: Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $f^{\prime\prime}=0, f^{\prime\prime\prime}\ne0$
$\qquad\:\:$ $ f^{\prime\prime}=0 \iff \begin{cases} 2x=0 \longrightarrow x_2=0\\ \\ e^{-2x}=0\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Möglicher Wendepunkt bei $x_w=0$
$\qquad\:\:$ Nullstelle der zweiten Ableitung in dritte einsetzen:
$\qquad\:\:$ $ f^{\prime\prime\prime}(0)=2e^{-2(0)}\cdot [1-2(0)]=2>0 \longrightarrow Recht-Links-Wendepunkt $
$\qquad\:\:$ Der Wendepunkt beträgt: $\underline{W(0|0,5)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\: Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ $ t_w: f^\prime(x_w)\cdot (x-x_w)+f(x_w) $ mit $ \begin{cases} x_w=0\\ \\ f^\prime(0)=-\frac{1}{2}\\ \\ f(0)=\frac{1}{2} \end{cases} $
$\qquad\qquad$ $ t_w=-\frac{1}{2}(x-0)+\frac{1}{2}=\underline{-\frac{1}{2}x+\frac{1}{2}} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\: Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=-\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $

$f(x)=x^2\cdot e^{-x}$
Lösung
$f(x)=x^2\cdot e^{-x}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ D_f=\forall x\: \begin{cases} x^2\in \mathbb{R}\\ \\ e^{-x}\in \mathbb{R} \end{cases} \:\: \longrightarrow \:\: \underline { D_f=]-\infty;+\infty[ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertesbereich\: ermitteln $
$\qquad\:\:$ $ W_f=\forall y \in \mathbb{R}, \:0\leq y\: \longrightarrow\: \underline { W_f=[0;+\infty[ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung: $ $
$\qquad\qquad$ $ f(x)=x^2\cdot e^{-x} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\:|\:\: \begin{cases} u(x)=x^2\: \longrightarrow \: u^\prime(x)=2x\\ \\ v(x)=e^{-x}\: \longrightarrow \:v^\prime(x)=-e^{-x} \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=2x\cdot e^{-x}+ x^2\cdot (-e^{-x}) $
$\qquad\qquad\qquad\:\:$ $ =\underline{e^{-x}\cdot (2x-x^2)} $
$\qquad\:\:$ Zweite Ableitung: $ $
$\qquad\qquad$ $ f^\prime(x)=e^{-x}\cdot (2x-x^2) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\:|\:\: \begin{cases} u(x)=e^{-x}\: \longrightarrow \: u^\prime(x)=-e^{-x}\\ \\ v(x)=(2x-x^2)\: \longrightarrow \:v^\prime(x)=2-2x \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-e^{-x}\cdot (2x-x^2)+ e^{-x}\cdot (2-2x) $
$\qquad\qquad\qquad\:\:$ $ =e^{-x}\cdot [-(2x-x^2)+(2-2x)] $
$\qquad\qquad\qquad\:\:$ $ =\underline{e^{-x}\cdot (x^2-4x+2)} $
$\qquad\:\:$ Dritte Ableitung: $ $
$\qquad\qquad$ $ f^{\prime\prime}(x)=e^{-x}\cdot (x^2-4x+2) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\:|\:\: \begin{cases} u(x)=e^{-x}\: \longrightarrow \: u^\prime(x)=-e^{-x}\\ \\ v(x)=(x^2-4x+2)\: \longrightarrow \:v^\prime(x)=2x-4 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=-e^{-x}\cdot (x^2-4x+2)+ e^{-x}\cdot (2x-4) $
$\qquad\qquad\qquad\:\:$ $ =-e^{-x}\cdot [(x^2-4x+2)-(2x-4)] $
$\qquad\qquad\qquad\:\:$ $ =\underline{-e^{-x}\cdot (x^2-6x+6)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=(0)^2\cdot e^{-0}\:\longrightarrow \: \underline{S_y(0|0)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen \:(Schnittpunkte\: mit\: der\: x-Achse:\: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0) \iff x^2\cdot e^{-x}=0 \Longrightarrow \begin{cases} x^2=0\: \longrightarrow\: x=0\\ \\ e^{-x}=0\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Es gibt eine Nullstelle an der Stelle $\underline{N_0=(0|0)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=(-x)^2\cdot e^{-(-x)}=x^2\cdot e^{x} $
$\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ \neq f(x) \:\: \longrightarrow \:\: $ keine Achsensymmetrie
$\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ \neq -f(x) \:\: \longrightarrow \:\: $ keine Punktsymmetrie
$\qquad\:\:$ $ f(x)=x^2\cdot e^{-x} $ ist weder achsensymmetrisch noch punktsymmetrisch
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\:Extrempunkte\: untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $ f^\prime(x)=0,\: f^{\prime\prime}(x) \neq0 $
$\qquad\:\:$ $ f^\prime(x)=0 \iff e^{-x}\cdot (2x-x^2)= 0 \iff \begin{cases} e^{-x}=0\: \textcolor{red}{n.L.}\\ \\ (2x-x^2)=0 \longrightarrow \begin{cases} x=0\\ \\ x=2 \end{cases} \end{cases} $
$\qquad\:\:$ Möglicher Extrempunkte bei $x_1=0$ und $x_2=2$
$\qquad\:\:$ Nullstellen der ersten Ableitung in zweite einsetzen:
$\qquad\qquad$ $ f^{\prime\prime}(0)=e^{-0}\cdot [0^2-4(0)+2]=>0 \longrightarrow Tiefpunkt $
$\qquad\qquad\qquad$ Der Tiefpunkt beträgt: $\underline{TP[0|f(0)]=(0|0)}$
$\qquad\qquad$ $ f^{\prime\prime}(2)=e^{-2}\cdot [x^2-4(2)+2]=-0,27<0 \longrightarrow Hochpunkt $
$\qquad\qquad\qquad$ Der Hochpunkt beträgt: $\underline{HP[2|f(2)]=(2|0,541)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\:Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $ f^{\prime\prime}(x)=0,\: f^{\prime\prime\prime} \neq 0 $
$\qquad\:\:$ $ f^{\prime\prime}(x)=0 \iff e^{-x}\cdot (x^2-4x+2)=0 \iff \begin{cases} e^{-x}=0\: \textcolor{red}{n.L.}\\ \\ (x^2-4x+2)=0\: (mit\: pq-Formel) \end{cases} $
$\qquad\:\:$ $ x_{1/2}=-\frac{-p}{2} \pm \sqrt{(\frac{-p}{2})^2-q} = -\frac{-4}{2} \pm \sqrt{(\frac{-4}{2})^2-2} =2\pm \sqrt{2} $
$\qquad\qquad\qquad$ $ \longrightarrow \begin{cases} x_1=2-\sqrt{2}=0,58\\ \\ x_2=2+\sqrt{2}=3,41 \end{cases} $
$\qquad\:\:$ Mögliche Wendepunkte bei $x_{w_1}=0,58$ und $x_{w_2}=3,41$
$\qquad\:\:$ Nullstellen der zweiten Ableitung in dritte einsetzen:
$\qquad\qquad$ $ f^{\prime\prime\prime}(0,58)=-1,599<0 \longrightarrow Links-Recht-Wendepunkt $
$\qquad\qquad$ $ f^{\prime\prime\prime}(3,41)=85,7>0 \longrightarrow Recht-Links-Wendepunkt $
$\qquad\:\:$ Die Wendepunkte sind: $\underline{W_1(0,58|0,19)\:}$ und $\: \underline{W_2(3,41|0,38)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\:Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ Für $W_1=0,58$; $ t_{w_1}: f^\prime(x_{w_1})\cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=0,58\\ \\ f^\prime(0,58)=0,46\\ \\ f(0,58)=0,19 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_1}=0,46(x-0,58)+0,19=0,46x-0,07} $
$\qquad\qquad$ Für $W_2=3,41$; $ t_{w_2}: f^\prime(x_{w_2})\cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=3,41\\ \\ f^\prime(3,41)=-0,16\\ \\ f(3,41)=0,38 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_2}=-0,16(x-3,41)+0,38=-0,16x+0,92} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\:Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=+\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $

$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 1.\: Definitionsbereich\: ermitteln $
$\qquad\:\:$ $ D_f=\forall x\: \begin{cases} x^2\in \mathbb{R}\\ \\ e^{-x}\in \mathbb{R} \end{cases} \:\: \longrightarrow \:\: \underline { D_f=]-\infty;+\infty[ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 2.\: Wertesbereich\: ermitteln $
$\qquad\:\:$ $ W_f=\forall y \in \mathbb{R}, \:0\leq y\: \longrightarrow\: \underline { W_f=[0;+\infty[ } $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 3.\: Ableitungen $
$\qquad\:\:$ Erste Ableitung: $ $
$\qquad\qquad$ $ f(x)=x^2\cdot e^{-x} $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^\prime(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\:|\:\: \begin{cases} u(x)=x^2\: \longrightarrow \: u^\prime(x)=2x\\ \\ v(x)=e^{-x}\: \longrightarrow \:v^\prime(x)=-e^{-x} \end{cases} $
$\qquad\qquad$ $ f^\prime(x)=2x\cdot e^{-x}+ x^2\cdot (-e^{-x}) $
$\qquad\qquad\qquad\:\:$ $ =\underline{e^{-x}\cdot (2x-x^2)} $
$\qquad\:\:$ Zweite Ableitung: $ $
$\qquad\qquad$ $ f^\prime(x)=e^{-x}\cdot (2x-x^2) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\:|\:\: \begin{cases} u(x)=e^{-x}\: \longrightarrow \: u^\prime(x)=-e^{-x}\\ \\ v(x)=(2x-x^2)\: \longrightarrow \:v^\prime(x)=2-2x \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime}(x)=-e^{-x}\cdot (2x-x^2)+ e^{-x}\cdot (2-2x) $
$\qquad\qquad\qquad\:\:$ $ =e^{-x}\cdot [-(2x-x^2)+(2-2x)] $
$\qquad\qquad\qquad\:\:$ $ =\underline{e^{-x}\cdot (x^2-4x+2)} $
$\qquad\:\:$ Dritte Ableitung: $ $
$\qquad\qquad$ $ f^{\prime\prime}(x)=e^{-x}\cdot (x^2-4x+2) $
$\qquad\qquad$ Mit Produktregel:
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=u^\prime(x)\cdot v(x)+u(x)\cdot v^\prime(x)\:\:|\:\: \begin{cases} u(x)=e^{-x}\: \longrightarrow \: u^\prime(x)=-e^{-x}\\ \\ v(x)=(x^2-4x+2)\: \longrightarrow \:v^\prime(x)=2x-4 \end{cases} $
$\qquad\qquad$ $ f^{\prime\prime\prime}(x)=-e^{-x}\cdot (x^2-4x+2)+ e^{-x}\cdot (2x-4) $
$\qquad\qquad\qquad\:\:$ $ =-e^{-x}\cdot [(x^2-4x+2)-(2x-4)] $
$\qquad\qquad\qquad\:\:$ $ =\underline{-e^{-x}\cdot (x^2-6x+6)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 4.\: Schnittpunkt\: mit\: der\: y-Achse:\: S_y(0|f(0)) $
$\qquad\:\:$ $ f(0)=(0)^2\cdot e^{-0}\:\longrightarrow \: \underline{S_y(0|0)} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 5.\: Nullstellen \:(Schnittpunkte\: mit\: der\: x-Achse:\: \longrightarrow y=f(x)=0 $
$\qquad\:\:$ $ f(x)=0) \iff x^2\cdot e^{-x}=0 \Longrightarrow \begin{cases} x^2=0\: \longrightarrow\: x=0\\ \\ e^{-x}=0\:\: \textcolor{red}{n.L.} \end{cases} $
$\qquad\:\:$ Es gibt eine Nullstelle an der Stelle $\underline{N_0=(0|0)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 6.\: Symmetrieverhalten\: untersuchen $
$\qquad\:\:$ $ f(-x)=(-x)^2\cdot e^{-(-x)}=x^2\cdot e^{x} $
$\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ \neq f(x) \:\: \longrightarrow \:\: $ keine Achsensymmetrie
$\qquad\qquad\qquad\qquad\qquad\qquad\:\:$ $ \neq -f(x) \:\: \longrightarrow \:\: $ keine Punktsymmetrie
$\qquad\:\:$ $ f(x)=x^2\cdot e^{-x} $ ist weder achsensymmetrisch noch punktsymmetrisch
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 7.\:Extrempunkte\: untersuchen $
$\qquad\:\:$ Notwendiges Kriterium: $ f^\prime(x)=0,\: f^{\prime\prime}(x) \neq0 $
$\qquad\:\:$ $ f^\prime(x)=0 \iff e^{-x}\cdot (2x-x^2)= 0 \iff \begin{cases} e^{-x}=0\: \textcolor{red}{n.L.}\\ \\ (2x-x^2)=0 \longrightarrow \begin{cases} x=0\\ \\ x=2 \end{cases} \end{cases} $
$\qquad\:\:$ Möglicher Extrempunkte bei $x_1=0$ und $x_2=2$
$\qquad\:\:$ Nullstellen der ersten Ableitung in zweite einsetzen:
$\qquad\qquad$ $ f^{\prime\prime}(0)=e^{-0}\cdot [0^2-4(0)+2]=>0 \longrightarrow Tiefpunkt $
$\qquad\qquad\qquad$ Der Tiefpunkt beträgt: $\underline{TP[0|f(0)]=(0|0)}$
$\qquad\qquad$ $ f^{\prime\prime}(2)=e^{-2}\cdot [x^2-4(2)+2]=-0,27<0 \longrightarrow Hochpunkt $
$\qquad\qquad\qquad$ Der Hochpunkt beträgt: $\underline{HP[2|f(2)]=(2|0,541)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 8.\:Wendepunkte\: untersuchen $
$\qquad\:\:$ Hinreichende Bedingung: $ f^{\prime\prime}(x)=0,\: f^{\prime\prime\prime} \neq 0 $
$\qquad\:\:$ $ f^{\prime\prime}(x)=0 \iff e^{-x}\cdot (x^2-4x+2)=0 \iff \begin{cases} e^{-x}=0\: \textcolor{red}{n.L.}\\ \\ (x^2-4x+2)=0\: (mit\: pq-Formel) \end{cases} $
$\qquad\:\:$ $ x_{1/2}=-\frac{-p}{2} \pm \sqrt{(\frac{-p}{2})^2-q} = -\frac{-4}{2} \pm \sqrt{(\frac{-4}{2})^2-2} =2\pm \sqrt{2} $
$\qquad\qquad\qquad$ $ \longrightarrow \begin{cases} x_1=2-\sqrt{2}=0,58\\ \\ x_2=2+\sqrt{2}=3,41 \end{cases} $
$\qquad\:\:$ Mögliche Wendepunkte bei $x_{w_1}=0,58$ und $x_{w_2}=3,41$
$\qquad\:\:$ Nullstellen der zweiten Ableitung in dritte einsetzen:
$\qquad\qquad$ $ f^{\prime\prime\prime}(0,58)=-1,599<0 \longrightarrow Links-Recht-Wendepunkt $
$\qquad\qquad$ $ f^{\prime\prime\prime}(3,41)=85,7>0 \longrightarrow Recht-Links-Wendepunkt $
$\qquad\:\:$ Die Wendepunkte sind: $\underline{W_1(0,58|0,19)\:}$ und $\: \underline{W_2(3,41|0,38)}$
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 9.\:Wendetangente\: bestimmen $
$\qquad\:\:$ Gleichung der Wendetangente:
$\qquad\qquad$ Für $W_1=0,58$; $ t_{w_1}: f^\prime(x_{w_1})\cdot (x-x_{w_1})+f(x_{w_1}) $ mit $ \begin{cases} x_{w_1}=0,58\\ \\ f^\prime(0,58)=0,46\\ \\ f(0,58)=0,19 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_1}=0,46(x-0,58)+0,19=0,46x-0,07} $
$\qquad\qquad$ Für $W_2=3,41$; $ t_{w_2}: f^\prime(x_{w_2})\cdot (x-x_{w_2})+f(x_{w_2}) $ mit $ \begin{cases} x_{w_2}=3,41\\ \\ f^\prime(3,41)=-0,16\\ \\ f(3,41)=0,38 \end{cases} $
$\qquad\qquad\qquad$ $ \underline{t_{w_2}=-0,16(x-3,41)+0,38=-0,16x+0,92} $
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize 10.\:Verhalten\: im\: Unendlichen $
$\qquad\:\:$ $ \lim\limits_{x\to -\infty} f(x)=+\infty \:\:\:\: | \:\:\:\: \lim\limits_{x\to +\infty} f(x)=0 $

Analytische Geometrie / Abi Berlin
Übungsaufgaben
Lösung
a) Zeige, dass das Viereck $ABFE$ ein Trapez ist.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: die\: Länge\: AE\: und\: BF $
$\qquad$ $ |\overline{AE}|=\sqrt{(0-0)^2+(40-0)^2+(120-0)^2}=126,491 $
$\qquad$ $ |\overline{BF}|=\sqrt{(0-0)^2+(58-20)^2+(114-0)^2}=120,166 $
$\qquad$ $ \large \frac {\overline{AE}} {\overline{BF}} = \frac{126,491}{120,166} $ $ \large = \frac{20}{19} $ $ \iff 20\cdot \overline{BF}=19\cdot \overline{AE} $
$\qquad\qquad\qquad\qquad\qquad\qquad$ $ \iff \overline{BF}= \large \frac{19}{20} \cdot $ $ \overline{AE} $
$\qquad\qquad\qquad\qquad\qquad\qquad$ $ \iff \overline{BF} \parallel \overline{AE} \:\: \longrightarrow \:\: ABFE $ ist ein Trapez.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Prüfe\: ob\: das\: Viereck\: im\: E\: einen\: rechten\: Winkel\: hat $
$\qquad$ Berechene das Skalarprodukt von $\overrightarrow{AE}$ und $\overrightarrow{EF}$
$\qquad\qquad$ $ \overrightarrow{AE} = \begin{pmatrix} 0-0\\40-0\\120-0 \end{pmatrix} = \begin{pmatrix} 0\\40\\120 \end{pmatrix} \:\:\:\: | \:\:\:\: \overrightarrow{EF} = \begin{pmatrix} 0-0\\58-40\\114-120 \end{pmatrix} = \begin{pmatrix} 0\\18\\-6 \end{pmatrix} $
$\qquad\qquad$ $ \overrightarrow{AE} \cdot \overrightarrow{EF} = \begin{pmatrix} 0\\40\\120 \end{pmatrix} \cdot \begin{pmatrix} 0\\18\\-6 \end{pmatrix} = 0\cdot 0+40\cdot 18+120\cdot (-6)=0 $
$\qquad\qquad$ $ \longrightarrow $ das Viereck hat im Punkt $E$ einen rechten Winkel.
b) Liegen $L$ und $M$ auf $AE$ bzw. $BF$ und verläuft $LM$ parallel zu $AB$ durch den Mittel-punkt von $EF$ , so ist der Flächeninhalt des Vierecks $ABFE$ ebenso groß wie der Flächeninhalt des Parallelogramms $ABML$. Betrachtet man $AB$ als dessen Grund- seite, so ist die zugehörige Höhe der Mittelwert der $z$-Koordinaten von $E$ und $F$. Die untere Teilfläche ist ein Parallelogramm, dessen Höhe zur Grundseite $AB$ halb so groß ist wie die des Parallelogramms $ABML$.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: die\: Länge\: AE\: und\: BF $
$\qquad$ $ |\overline{AE}|=\sqrt{(0-0)^2+(40-0)^2+(120-0)^2}=126,491 $
$\qquad$ $ |\overline{BF}|=\sqrt{(0-0)^2+(58-20)^2+(114-0)^2}=120,166 $
$\qquad$ $ \large \frac {\overline{AE}} {\overline{BF}} = \frac{126,491}{120,166} $ $ \large = \frac{20}{19} $ $ \iff 20\cdot \overline{BF}=19\cdot \overline{AE} $
$\qquad\qquad\qquad\qquad\qquad\qquad$ $ \iff \overline{BF}= \large \frac{19}{20} \cdot $ $ \overline{AE} $
$\qquad\qquad\qquad\qquad\qquad\qquad$ $ \iff \overline{BF} \parallel \overline{AE} \:\: \longrightarrow \:\: ABFE $ ist ein Trapez.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Prüfe\: ob\: das\: Viereck\: im\: E\: einen\: rechten\: Winkel\: hat $
$\qquad$ Berechene das Skalarprodukt von $\overrightarrow{AE}$ und $\overrightarrow{EF}$
$\qquad\qquad$ $ \overrightarrow{AE} = \begin{pmatrix} 0-0\\40-0\\120-0 \end{pmatrix} = \begin{pmatrix} 0\\40\\120 \end{pmatrix} \:\:\:\: | \:\:\:\: \overrightarrow{EF} = \begin{pmatrix} 0-0\\58-40\\114-120 \end{pmatrix} = \begin{pmatrix} 0\\18\\-6 \end{pmatrix} $
$\qquad\qquad$ $ \overrightarrow{AE} \cdot \overrightarrow{EF} = \begin{pmatrix} 0\\40\\120 \end{pmatrix} \cdot \begin{pmatrix} 0\\18\\-6 \end{pmatrix} = 0\cdot 0+40\cdot 18+120\cdot (-6)=0 $
$\qquad\qquad$ $ \longrightarrow $ das Viereck hat im Punkt $E$ einen rechten Winkel.
b) Liegen $L$ und $M$ auf $AE$ bzw. $BF$ und verläuft $LM$ parallel zu $AB$ durch den Mittel-punkt von $EF$ , so ist der Flächeninhalt des Vierecks $ABFE$ ebenso groß wie der Flächeninhalt des Parallelogramms $ABML$. Betrachtet man $AB$ als dessen Grund- seite, so ist die zugehörige Höhe der Mittelwert der $z$-Koordinaten von $E$ und $F$. Die untere Teilfläche ist ein Parallelogramm, dessen Höhe zur Grundseite $AB$ halb so groß ist wie die des Parallelogramms $ABML$.
Stochastik - Abi Berlin
Übungsaufgaben
-
In einer Urne befinde sich $4$ schwarze und $6$ weiße Kugeln. Aus der Urne werden nacheinander und ohne Zurücklegen $3$ Kugel gezogen.
a) Ermittle die Wahrscheinlichkeit dafür, dass alle drei gezogenen Kugeln schwarz sind.
b) Weisen Sie nach, dass die Wahrscheinlichkeit dafür, dass unter den $3$ gezogenen
$\:\:\:\:\:\:$Kugeln mindestens $2$ schwarze Kugeln sind, genau $\frac{1}{3}$ beträgt.
Lösung$4$ schwarze und $6$ weiße Kugeln. $3$ Kugeln gezogen, nacheinander und ohne Zurücklegen.
$\:\:$ a) Wahrscheinlichkeit dafür, dass alle 3 gezogenen Kugeln schwarz sind.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Schreibe\: die\: Wahrscheinlichkeit\: für\: schwarze\: und\: weiße\: Kugeln $
$\qquad$ Gesamt Kugeln: $P(A)=10$
$\qquad\qquad\qquad$ $ P_{SK}= \large \frac{4}{10}\qquad|\qquad P_{WK}= \large \frac{6}{10} $
$\qquad$ Alle 3 gezogenen Kugeln sind schwarz $\Longrightarrow\:\: 3\times P_{SK}$
$\qquad\qquad\qquad$ $ 3 \times P_{SK} \large =\frac{4}{10}\cdot \frac{3}{9}\cdot \frac{2}{8} =\frac{2}{5}\cdot \frac{1}{3}\cdot \frac{1}{4} =\frac{1}{30} $
$\:\:$ b) Wahrscheinlichkeit dafür, dass mindestens 2 der gezogenen Kugeln sind schwarz
$\qquad$ $ P_{\ge2} = P_{SK}\cdot P_{SK}\cdot P_{SK} + P_{SK}\cdot P_{SK}\cdot P_{WK} + P_{SK}\cdot P_{WK}\cdot P_{SK} + P_{WK}\cdot P_{SK}\cdot P_{SK} $
$\qquad\qquad$ $ \iff \large \frac{1}{30} + \frac{4}{10}\cdot \frac{3}{9}\cdot \frac{6}{8} + \frac{4}{10}\cdot \frac{3}{9}\cdot \frac{6}{8} + \frac{4}{10}\cdot \frac{3}{9}\cdot \frac{6}{8} $
$\qquad\qquad$ $ \iff \large \frac{1}{30} + 3\cdot \frac{2}{5}\cdot \frac{1}{3}\cdot \frac{3}{4} $
$\qquad\qquad$ $ \iff \large \frac{1}{30} + 3\cdot \frac{1}{10} $
$\qquad\qquad$ $ \iff \large \frac{1}{30} + \frac{9}{30} = \frac{10}{30} = \frac{1}{3} $
Baumdiagramm
-
Lösunga) Wahrscheinlichkeit dafür, dass die Augensumme 6 beträgt.
$ \:\:\: $ $ \: \Large \Bigg\downarrow $ $ \normalsize Berechne\: die\: Wahrscheinlichkeit\: für\: die\: Seite\: 1\: und\: 5 $
$\qquad$ Wahrscheinlichkeit dafür, dass die Seite 1 beträgt: $p_1=\frac{1}{2}$
$\qquad$ Wahrscheinlichkeit dafür, dass die Seite 5 beträgt: $p_5=\frac{1}{2}$
$ \:\:\: $ $ P(AS=6) \large = p_1\cdot p_5+p_5\cdot p_1 = \frac{1}{2}\cdot \frac{1}{2} + \frac{1}{2}\cdot \frac{1}{2} = \frac{1}{2} $
a) Erwartungswert der Auszahlung
$\qquad$ Weil $ P(AS=2)=P(AS=10) = \frac{1}{4}, $
$\qquad$ ergibt sich:$\:\:$ $ E = \frac{1}{4}\cdot 2 + \frac{1}{2}\cdot 6 + \frac{1}{4}\cdot 10 =3 $
Wenn der Einsatz 3€ beträgt, wird der Erwartungswert für den Gewinn null.
$\iff$ Das Spiel fair. -
Lösunga) Wahrscheinlichkeit dafür, dass es gleichzeitig Stau an Baustelle 2 und 3 gibt.
$\qquad$ $ P_{(Stau\: an\: Baustelle\: 2/3)} \large = \frac{1}{3} \cdot \frac{1}{5} = \frac{1}{15} $
b) Wahrscheinlichkeit dafür, dass es kein Stau gibt.
$\qquad$ $ P_{(Kein\: Stau)} = P_{(1-Frei/2-Frei/3-Frei)} + P_{(1-Frei/2-Frei/3-Stau)} + P_{(1-Frei/2-Stau/3-Frei)} $
$\qquad\qquad\qquad\:\:\:\:$ $ \large = \frac{3}{4} \cdot \frac{2}{3} \cdot \frac{4}{5} + \frac{3}{4} \cdot \frac{2}{3} \cdot \frac{1}{5} + \frac{3}{4} \cdot \frac{1}{3} \cdot \frac{4}{5} $
$\qquad\qquad\qquad\:\:\:\:$ $ \large = \frac{42}{60} = \frac{7}{10} $ -
Ein Landwirt verpackt Eier in Packungen zu jeweils $6$ Stück. Bei einer Kontrolle wird festge-
stellt, dass bei 5% der verpackten Eier die Schale beschädigt ist.
a) Gebe im Sachzusammenhang ein Ereignis $E$ an, für das die Wahrscheinlichkeit durch $P(E)=1-(0,95)^6$ ermittelt werden kann.
b) Bei einer genaueren Kontrolle wird zusätzlich registriert, ob die beschädigten Eier eine weiße oder eine braune Schale haben. Daraus ergibt sich folgende unvollständige Vier- feldertafel:
Schale weiß Schale braun Schale beschädigt 150 350 Schale nicht beschädigt 10 000
Lösunga) $E:$ Mindestens ein Ei in einer 6er-Packung ist beschädigt.
b)Schale weiß Schale braun Schale beschädigt 150 350 500 Schale nicht beschädigt 2850 6650 9500 3000 7000 10 000